第15页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
1. 如图,$\angle ACD$ 是 $\triangle ABC$ 的外角,若 $\angle ACD = 110^{\circ}$,$\angle B = 50^{\circ}$,则 $\angle A$ 的度数为 (
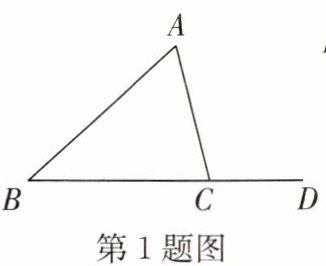
A.$40^{\circ}$
B.$50^{\circ}$
C.$55^{\circ}$
D.$60^{\circ}$
D
)
A.$40^{\circ}$
B.$50^{\circ}$
C.$55^{\circ}$
D.$60^{\circ}$
答案:
D
2. 若一个三角形的一个外角小于与它相邻的内角,则这个三角形是 (
A.直角三角形
B.锐角三角形
C.钝角三角形
D.无法确定
C
)A.直角三角形
B.锐角三角形
C.钝角三角形
D.无法确定
答案:
C
3. 如图,$\angle DBA = 105^{\circ}$,$\angle ECA = 125^{\circ}$,则 $\angle A$ 的度数为
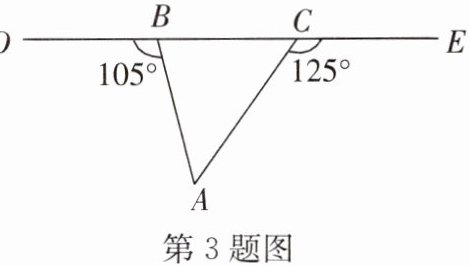
50°
.
答案:
50°
题型 1 如图,$\angle 1$,$\angle 2$,$\angle 3$ 的大小关系为 (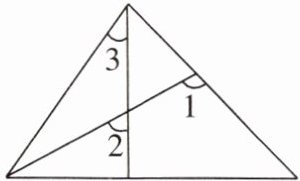
A.$\angle 2 > \angle 1 > \angle 3$
B.$\angle 1 > \angle 3 > \angle 2$
C.$\angle 3 > \angle 2 > \angle 1$
D.$\angle 1 > \angle 2 > \angle 3$
D
)
A.$\angle 2 > \angle 1 > \angle 3$
B.$\angle 1 > \angle 3 > \angle 2$
C.$\angle 3 > \angle 2 > \angle 1$
D.$\angle 1 > \angle 2 > \angle 3$
答案:
D
题型 2 如图,$\angle A = 65^{\circ}$,$\angle B = 75^{\circ}$,将 $\triangle ABC$ 沿 $EF$ 折叠,使点 $C$ 落到点 $C'$ 处,若 $\angle 1 = 20^{\circ}$,则 $\angle 2 = $______.
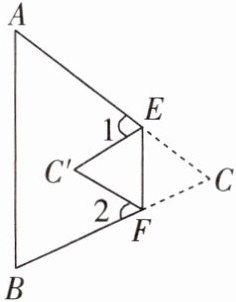

答案:
1. 首先,根据三角形内角和定理:
在$\triangle ABC$中,已知$\angle A = 65^{\circ}$,$\angle B = 75^{\circ}$,由三角形内角和公式$\angle A+\angle B+\angle C = 180^{\circ}$,可得$\angle C=180^{\circ}-\angle A - \angle B$。
把$\angle A = 65^{\circ}$,$\angle B = 75^{\circ}$代入,得$\angle C=180^{\circ}-65^{\circ}-75^{\circ}=40^{\circ}$。
2. 然后,根据折叠的性质:
因为$\triangle EFC'$是由$\triangle EFC$折叠得到的,所以$\angle C'=\angle C = 40^{\circ}$。
在四边形$ABFE$中,$\angle A+\angle B+\angle BFE+\angle AEF = 360^{\circ}$,在$\triangle EFC'$中,$\angle C'+\angle 1+\angle 2+\angle BFE+\angle AEF = 360^{\circ}$(这里$\angle BFE+\angle AEF$是公共部分)。
又因为$\angle A+\angle B+\angle C=180^{\circ}$,$\angle C'+\angle 1+\angle 2+\angle C = 180^{\circ}$(根据四边形内角和与三角形内角和的关系转化)。
已知$\angle C=\angle C' = 40^{\circ}$,$\angle 1 = 20^{\circ}$。
由$\angle 1+\angle 2 + 2\angle C=180^{\circ}$($\angle C=\angle C'$,折叠后$\angle C$的度数不变,相当于两个$\angle C$与$\angle 1$、$\angle 2$组成一个平角)。
3. 最后,求解$\angle 2$:
把$\angle C = 40^{\circ}$,$\angle 1 = 20^{\circ}$代入$\angle 1+\angle 2 + 2\angle C=180^{\circ}$,得到$20^{\circ}+\angle 2+2×40^{\circ}=180^{\circ}$。
即$\angle 2+20^{\circ}+80^{\circ}=180^{\circ}$。
移项可得$\angle 2=180^{\circ}-(20^{\circ} + 80^{\circ})$。
所以$\angle 2 = 60^{\circ}$。
故答案为$60^{\circ}$。
在$\triangle ABC$中,已知$\angle A = 65^{\circ}$,$\angle B = 75^{\circ}$,由三角形内角和公式$\angle A+\angle B+\angle C = 180^{\circ}$,可得$\angle C=180^{\circ}-\angle A - \angle B$。
把$\angle A = 65^{\circ}$,$\angle B = 75^{\circ}$代入,得$\angle C=180^{\circ}-65^{\circ}-75^{\circ}=40^{\circ}$。
2. 然后,根据折叠的性质:
因为$\triangle EFC'$是由$\triangle EFC$折叠得到的,所以$\angle C'=\angle C = 40^{\circ}$。
在四边形$ABFE$中,$\angle A+\angle B+\angle BFE+\angle AEF = 360^{\circ}$,在$\triangle EFC'$中,$\angle C'+\angle 1+\angle 2+\angle BFE+\angle AEF = 360^{\circ}$(这里$\angle BFE+\angle AEF$是公共部分)。
又因为$\angle A+\angle B+\angle C=180^{\circ}$,$\angle C'+\angle 1+\angle 2+\angle C = 180^{\circ}$(根据四边形内角和与三角形内角和的关系转化)。
已知$\angle C=\angle C' = 40^{\circ}$,$\angle 1 = 20^{\circ}$。
由$\angle 1+\angle 2 + 2\angle C=180^{\circ}$($\angle C=\angle C'$,折叠后$\angle C$的度数不变,相当于两个$\angle C$与$\angle 1$、$\angle 2$组成一个平角)。
3. 最后,求解$\angle 2$:
把$\angle C = 40^{\circ}$,$\angle 1 = 20^{\circ}$代入$\angle 1+\angle 2 + 2\angle C=180^{\circ}$,得到$20^{\circ}+\angle 2+2×40^{\circ}=180^{\circ}$。
即$\angle 2+20^{\circ}+80^{\circ}=180^{\circ}$。
移项可得$\angle 2=180^{\circ}-(20^{\circ} + 80^{\circ})$。
所以$\angle 2 = 60^{\circ}$。
故答案为$60^{\circ}$。
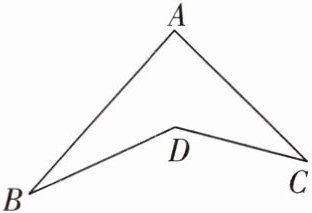
题型 3 如图,求证:$\angle BDC = \angle B + \angle C + \angle BAC$.(方法指导:添加辅助线,由三角形的内角和定理的推论求几个角之间的关系)

答案:
解:
延长 $BD$ 交 $AC$ 于点 $E$。
因为$\angle BEC$是$\triangle ABE$的外角,根据三角形外角的性质:三角形的一个外角等于与它不相邻的两个内角之和,所以$\angle BEC=\angle B + \angle BAC$。
又因为$\angle BDC$是$\triangle DEC$的外角,同理可得$\angle BDC=\angle BEC+\angle C$。
把$\angle BEC=\angle B + \angle BAC$代入$\angle BDC=\angle BEC+\angle C$中,得到$\angle BDC=\angle B + \angle C+\angle BAC$。
综上,$\angle BDC = \angle B + \angle C + \angle BAC$得证。
延长 $BD$ 交 $AC$ 于点 $E$。
因为$\angle BEC$是$\triangle ABE$的外角,根据三角形外角的性质:三角形的一个外角等于与它不相邻的两个内角之和,所以$\angle BEC=\angle B + \angle BAC$。
又因为$\angle BDC$是$\triangle DEC$的外角,同理可得$\angle BDC=\angle BEC+\angle C$。
把$\angle BEC=\angle B + \angle BAC$代入$\angle BDC=\angle BEC+\angle C$中,得到$\angle BDC=\angle B + \angle C+\angle BAC$。
综上,$\angle BDC = \angle B + \angle C + \angle BAC$得证。
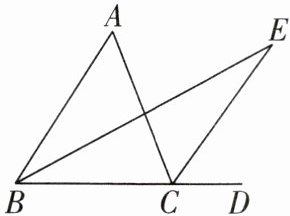
题型 4 如图,$D$ 是 $BC$ 延长线上一点,$\angle ABC$,$\angle ACD$ 的平分线交于点 $E$,试探究 $\angle E$ 与 $\angle A$ 有何数量关系,并证明.

答案:
解:$\angle E=\frac{1}{2}\angle A$。
证明:设$\angle ABC = 2x$,$\angle ACD = 2y$。
因为$BE$平分$\angle ABC$,$CE$平分$\angle ACD$,所以$\angle EBC=x$,$\angle ECD = y$。
根据三角形外角性质,$\angle ACD=\angle A+\angle ABC$,即$2y=\angle A + 2x$ ①;
又因为$\angle ECD=\angle E+\angle EBC$,即$y=\angle E+x$ ②。
将②式两边同时乘以$2$得$2y = 2\angle E+2x$ ③。
把①式$2y=\angle A + 2x$代入③式可得:$\angle A + 2x=2\angle E+2x$,
两边同时减去$2x$,得到$\angle E=\frac{1}{2}\angle A$。
综上,$\angle E$与$\angle A$的数量关系为$\boldsymbol{\angle E=\frac{1}{2}\angle A}$。
证明:设$\angle ABC = 2x$,$\angle ACD = 2y$。
因为$BE$平分$\angle ABC$,$CE$平分$\angle ACD$,所以$\angle EBC=x$,$\angle ECD = y$。
根据三角形外角性质,$\angle ACD=\angle A+\angle ABC$,即$2y=\angle A + 2x$ ①;
又因为$\angle ECD=\angle E+\angle EBC$,即$y=\angle E+x$ ②。
将②式两边同时乘以$2$得$2y = 2\angle E+2x$ ③。
把①式$2y=\angle A + 2x$代入③式可得:$\angle A + 2x=2\angle E+2x$,
两边同时减去$2x$,得到$\angle E=\frac{1}{2}\angle A$。
综上,$\angle E$与$\angle A$的数量关系为$\boldsymbol{\angle E=\frac{1}{2}\angle A}$。
查看更多完整答案,请扫码查看


