第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
4. 在 $\triangle ABC$ 中,$\angle A = 70^{\circ}-\angle B$,则 $\angle C$ 的度数为(
A.$35^{\circ}$
B.$70^{\circ}$
C.$110^{\circ}$
D.$140^{\circ}$
C
)A.$35^{\circ}$
B.$70^{\circ}$
C.$110^{\circ}$
D.$140^{\circ}$
答案:
C
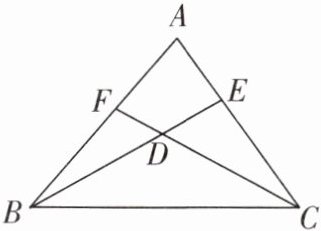
5. 如图,$F$ 是 $AB$ 上一点,$E$ 是 $AC$ 上一点,$BE$,$CF$ 相交于点 $D$,$\angle A = 70^{\circ}$,$\angle ACF = 30^{\circ}$,$\angle ABE = 20^{\circ}$,则 $\angle BDC$ 的度数为(
A.$172^{\circ}$
B.$80^{\circ}$
C.$120^{\circ}$
D.$60^{\circ}$
C
)
A.$172^{\circ}$
B.$80^{\circ}$
C.$120^{\circ}$
D.$60^{\circ}$
答案:
C
6. 在 $\triangle ABC$ 中,$\angle A = 20^{\circ}$,$\angle B = 4\angle C$,则 $\angle C$ 的度数为
32°
。
答案:
32°
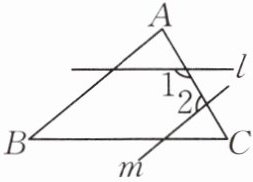
7. 如图,直线 $l$,$m$ 分别与 $\triangle ABC$ 的边 $BC$,$AB$ 平行,$\angle 1 = 120^{\circ}$,$\angle 2 = 100^{\circ}$,则 $\angle B$ 的度数是(
A.$70^{\circ}$
B.$60^{\circ}$
C.$50^{\circ}$
D.$40^{\circ}$
D
)
A.$70^{\circ}$
B.$60^{\circ}$
C.$50^{\circ}$
D.$40^{\circ}$
答案:
D
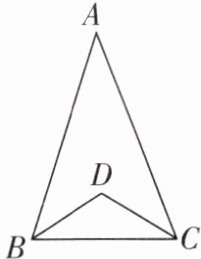
8. 如图,把三角形铁皮 $ABC$ 加工成四边形 $ABCD$ 形状的零件,$\angle A = 40^{\circ}$,且 $D$ 恰好是 $\triangle ABC$ 两条角平分线的交点,工人师傅量得 $\angle BDC = 110^{\circ}$,则这个四边形零件加工
合格
。(填“合格”或“不合格”)
答案:
合格
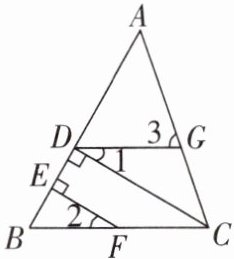
9. 如图,$CD\perp AB$ 于点 $D$,且 $CD$ 平分 $\angle ACB$,$F$ 是 $BC$ 上任意一点,$FE\perp AB$ 于点 $E$,且 $\angle 1= \angle 2$。
(1)求证:$\angle 3= \angle ACB$。
(2)若 $\angle 3 = 86^{\circ}$,求 $\angle B$ 的度数。
(1)求证:$\angle 3= \angle ACB$。
(2)若 $\angle 3 = 86^{\circ}$,求 $\angle B$ 的度数。

答案:
解:
(1)证明:
∵CD⊥AB,FE⊥AB,
∴CD//FE,
∴∠2=∠BCD.
∵∠1=∠2,
∴∠1=∠BCD,
∴BC//DG,
∴∠3=∠ACB.
(2)
∵∠ACB=∠3=86°,CD平分∠ACB,
∴∠BCD=$\frac{1}{2}$∠ACB=43°.又
∵∠B+∠BCD=90°,
∴∠B=47°.
(1)证明:
∵CD⊥AB,FE⊥AB,
∴CD//FE,
∴∠2=∠BCD.
∵∠1=∠2,
∴∠1=∠BCD,
∴BC//DG,
∴∠3=∠ACB.
(2)
∵∠ACB=∠3=86°,CD平分∠ACB,
∴∠BCD=$\frac{1}{2}$∠ACB=43°.又
∵∠B+∠BCD=90°,
∴∠B=47°.
10. 小亮在学习中遇到这样一个问题:
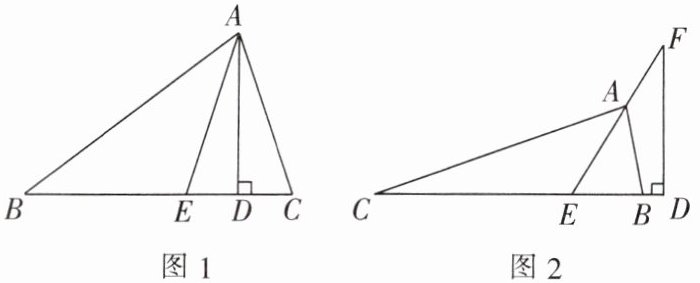
如图1,在 $\triangle ABC$ 中,$\angle C>\angle B$,$AE$ 平分 $\angle BAC$,$AD\perp BC$ 于点 $D$。
猜想 $\angle B$,$\angle C$,$\angle EAD$ 的数量关系,并说明理由。
(1)小亮阅读题目后,没有发现数量关系与解题思路。于是尝试代入 $\angle B$,$\angle C$ 的值求 $\angle EAD$,得到下面几组对应值:
| $\angle B/$度 | $10$ | $30$ | $30$ | $20$ | $20$ |
| $\angle C/$度 | $70$ | $70$ | $60$ | $60$ | $80$ |
| $\angle EAD/$度 | $30$ | $20$ | $15$ | $a$ | $30$ |
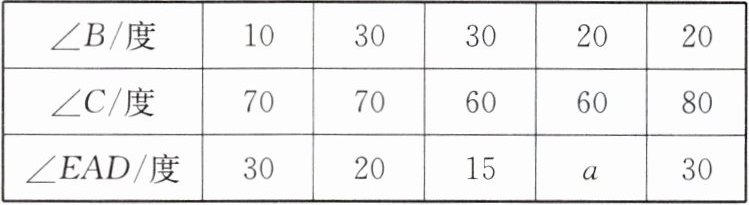
上表中 $a = $
(3)小亮突发奇想,交换 $B$,$C$ 两个字母位置,如图2,过 $EA$ 的延长线作 $FD\perp BC$ 交 $CB$ 的延长线于点 $D$,当 $\angle B = 80^{\circ}$,$\angle C = 20^{\circ}$ 时,求 $\angle F$ 的度数。
如图1,在 $\triangle ABC$ 中,$\angle C>\angle B$,$AE$ 平分 $\angle BAC$,$AD\perp BC$ 于点 $D$。
猜想 $\angle B$,$\angle C$,$\angle EAD$ 的数量关系,并说明理由。

(1)小亮阅读题目后,没有发现数量关系与解题思路。于是尝试代入 $\angle B$,$\angle C$ 的值求 $\angle EAD$,得到下面几组对应值:
| $\angle B/$度 | $10$ | $30$ | $30$ | $20$ | $20$ |
| $\angle C/$度 | $70$ | $70$ | $60$ | $60$ | $80$ |
| $\angle EAD/$度 | $30$ | $20$ | $15$ | $a$ | $30$ |

上表中 $a = $
20
。(3)小亮突发奇想,交换 $B$,$C$ 两个字母位置,如图2,过 $EA$ 的延长线作 $FD\perp BC$ 交 $CB$ 的延长线于点 $D$,当 $\angle B = 80^{\circ}$,$\angle C = 20^{\circ}$ 时,求 $\angle F$ 的度数。
答案:
解:
(1)20.
(2)猜想:∠EAD=$\frac{1}{2}$(∠C−∠B).理由:
∵AD⊥BC,
∴∠DAC=90°−∠C.
∵AE平分∠BAC,∠BAC=180°−∠B−∠C,
∴∠EAC=$\frac{1}{2}$∠BAC=90°−$\frac{1}{2}$∠B−$\frac{1}{2}$∠C,
∴∠EAD=∠EAC−∠DAC=90°−$\frac{1}{2}$∠B −$\frac{1}{2}$∠C−(90°−∠C)=$\frac{1}{2}$(∠C−∠B).
(3)如图,过点A作AH⊥CD于点H.
∵AH⊥CD,FD⊥CD,
∴AH//DF,
∴∠F=∠EAH=$\frac{1}{2}$(∠B−∠C)=$\frac{1}{2}$(80°−20°)=30°.
(1)20.
(2)猜想:∠EAD=$\frac{1}{2}$(∠C−∠B).理由:
∵AD⊥BC,
∴∠DAC=90°−∠C.
∵AE平分∠BAC,∠BAC=180°−∠B−∠C,
∴∠EAC=$\frac{1}{2}$∠BAC=90°−$\frac{1}{2}$∠B−$\frac{1}{2}$∠C,
∴∠EAD=∠EAC−∠DAC=90°−$\frac{1}{2}$∠B −$\frac{1}{2}$∠C−(90°−∠C)=$\frac{1}{2}$(∠C−∠B).
(3)如图,过点A作AH⊥CD于点H.
∵AH⊥CD,FD⊥CD,
∴AH//DF,
∴∠F=∠EAH=$\frac{1}{2}$(∠B−∠C)=$\frac{1}{2}$(80°−20°)=30°.
查看更多完整答案,请扫码查看


