《2025年新课程课堂同步练习册九年级数学上册人教版》

2. 如图9,AB为⊙O的直径,AB= AC,BC交⊙O于点D. 求证:BD= DC.

答案： 证明：
连接$AD$。
∵$AB$为$\odot O$的直径，
∴$\angle ADB = 90^{\circ}$（直径所对的圆周角是直角），
即$AD\perp BC$。
∵$AB = AC$，
∴$D$为$BC$的中点（等腰三角形三线合一），
∴$BD = DC$。

3. 如图10,△ABC内接于⊙O,BC= 12 cm,∠A= 60°. 求⊙O的直径.

答案：
解：连接$BO$并延长交$⊙O$于点$D，$连接$CD$　　

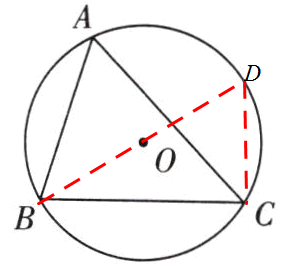
∵$BD$是$⊙O$的直径，$ $　　
∴$∠BCD=90°（$直径所对的圆周角是直角$）。$$ $　　
∵$∠A=60°，$$ $　　
∴$∠D=∠A=60°（$同弧所对的圆周角相等$）。$$ $　　
在$Rt△BCD$中，$BC=12cm，$$∠D=60°$　　
∴$∠DBC=30°，$
∴$BD=2CD$　　
∵$BC²+CD²=BD²$　　
∴$12^2+CD^2=(2CD)^2$　　
解得$CD=4\sqrt 3$　　
∴$BD=2CD=8\sqrt 3$　　
答：$⊙O$的直径为$8\sqrt 3 cm。$　　

1. ⊙O的半径为6,线段OP的长度为8,则点P与圆的位置关系是(B)
A.点P在圆上
B.点P在圆外
C.点P在圆内
D.无法确定

答案： B.点P在圆外。

2. 下面四个命题中真命题的个数有(C)
①经过三点一定可以作圆；
②任意一个三角形一定有一个外接圆,而且只有一个外接圆；
③任意一个圆一定有一个内接三角形,而且只有一个内接三角形；
④三角形的外心到三角形三个顶点的距离相等.
A.4
B.3
C.2
D.1

答案： C