《2025年新课程课堂同步练习册九年级数学上册人教版》

3. 如图4均为7×7的正方形网格,点A,B,C在格点上.
(1)在图4(1)中确定格点D,并画出以A,B,C,D为顶点的四边形,使其为轴对称图形(画一个即可).
(2)在图4(2)中确定格点E,并画出以A,B,C,E为顶点的四边形,使其为中心对称图形(画一个即可).

答案：
(1)图略（答案不唯一，只要画出的四边形沿某条直线对折后两边能重合即可，比如可以找到关于某条直线与ABC对称的D点构成轴对称四边形）。
(2)图略（答案不唯一，只要画出的四边形绕着某一点旋转$180^{\circ}$后能与自身重合即可，比如可以找到使得ABC绕某点旋转$180^{\circ}$后能与自身对应的E点构成中心对称四边形）。

4. 如图5,已知矩形ABCD和矩形AB'C'D'关于A点对称,试说明四边形BDB'D'是菱形.

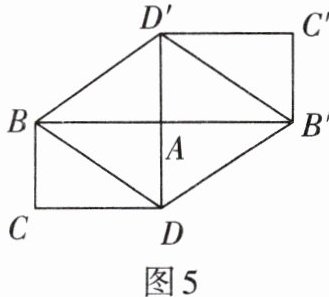
答案： 证明：
∵矩形ABCD和矩形AB'C'D'关于A点对称，
∴点B与点B'，点D与点D'关于点A对称，
∴AA为BB'和DD'的中点，即AB=AB'，AD=AD'，且BB'、DD'互相平分于点A，
∴四边形BDB'D'是平行四边形。
∵四边形ABCD是矩形，
∴∠BAD=90°，
∴在平行四边形BDB'D'中，对角线BB'⊥DD'，
∴平行四边形BDB'D'是菱形。

5. 如图6,在△ABC中,AB= AC,若将△ABC绕点C顺时针旋转180°得到△FEC.
(1)试猜想AE与BF有何关系,并说明理由.
(2)若△ABC的面积为$3cm^2,$求四边形ABFE的面积.
(3)当∠ACB为多少度时,四边形ABFE为矩形?请说明理由.

答案： 解：　　
$(1)AE//BF$且$AE=BF$　　
∵$△ABC$与$△FEC$关于点$C$对称　　
∴$AB//FE$且$AB=FE$　　
∴四边形$ABFE$是平行四边形　　
∴$AE//BF$且$AE=BF$　　
$(2)$　　
∵四边形$ABFE$是平行四边形　　
∴$BC=CE，$$AC=CF$　　
∴$S_{△ABE}=2S_{△ABC}=6{cm}^{2}$　　
∴$S_{四边形ABFE}=2S_{△ABE}=12{cm}^{2}$　　
$(3)$当$∠ACB=60°，$四边形$ABFE$为矩形，理由如下：　　
∵$∠ACB=60°，$$AB=AC$　　
∴$AB=AC=BC$　　
∵四边形$ABFE$是平行四边形　　
∴$AF=2AC，$$BE=2BC$　　
∴$AF=BE$　　
∴四边形$ABFE$为矩形