第32页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
4. 二次函数$y= -x^{2}+bx+c的图象的最高点是(-1,-3)$,则$b,c$的值是(
A.$b= 2,c= 4$
B.$b= 2,c= -4$
C.$b= -2,c= 4$
D.$b= -2,c= -4$
D
)A.$b= 2,c= 4$
B.$b= 2,c= -4$
C.$b= -2,c= 4$
D.$b= -2,c= -4$
答案:
D
5. 已知抛物线$y= ax^{2}+bx+c(a≠0)$在平面直角坐标系中的位置如图2所示,则下列结论中正确的是(
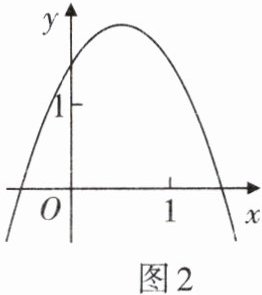
A.$a>0$
B.$b<0$
C.$c<0$
D.$a+b+c>0$
D
)
A.$a>0$
B.$b<0$
C.$c<0$
D.$a+b+c>0$
答案:
D
1. 抛物线$y= -2x^{2}+6x-1$的顶点坐标为
$(\frac{3}{2},\frac{7}{2})$
,对称轴为$x=\frac{3}{2}$
.
答案:
顶点坐标为$(\frac{3}{2},\frac{7}{2})$;对称轴为$x=\frac{3}{2}$。
2. 已知二次函数$y= \frac{1}{4}x^{2}-\frac{5}{2}x+6$,当$x= $
$5$
时,$y_{最小}= $$-\frac{1}{4}$
;当$x$$<5$
时,$y随x$的增大而减小.
答案:
$x = 5$;$y_{最小} = -\frac{1}{4}$;$x < 5$
3. 二次函数$y= ax^{2}+bx+c$的图象如图3所示,则$ac$
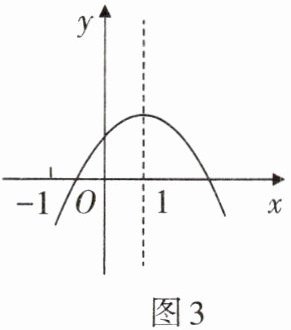
<
0(填“>”“<”或“=”).
答案:
<
4. 如图4,已知二次函数$y= x^{2}+bx+c的图象经过点(-1,0),(1,-2)$,当$y随x$的增大而增大时,$x$的取值范围是
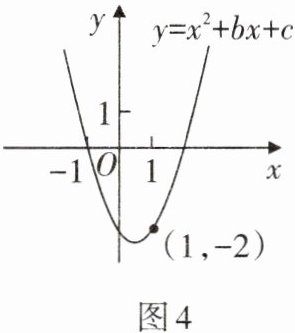
$x>\frac 1 2$
.
答案:
$x>\frac 1 2$
5. 已知二次函数$y= x^{2}-2x(-1≤x≤t-1)$,当$x= -1$时,函数取得最大值,当$x= 1$时,函数取得最小值,则$t$的取值范围是
$2 \leq t \leq 4$
。
答案:
$2 \leq t \leq 4$。
1. 用配方法把下列二次函数化为$y= a(x-h)^{2}+k$的形式:
(1)$y= x^{2}-8x+10$;
(2)$y= -3x^{2}+2x-1$;
(3)$y= ax^{2}+bx+c$.
(1)$y= x^{2}-8x+10$;
(2)$y= -3x^{2}+2x-1$;
(3)$y= ax^{2}+bx+c$.
答案:
(1)解:$y=x^{2}-8x+10$
$=x^{2}-8x+16 - 16 + 10$
$=(x - 4)^{2}-6$
(2)解:$y=-3x^{2}+2x - 1$
$=-3\left(x^{2}-\dfrac{2}{3}x\right)-1$
$=-3\left(x^{2}-\dfrac{2}{3}x+\dfrac{1}{9}-\dfrac{1}{9}\right)-1$
$=-3\left[\left(x - \dfrac{1}{3}\right)^{2}-\dfrac{1}{9}\right]-1$
$=-3\left(x - \dfrac{1}{3}\right)^{2}+\dfrac{1}{3}-1$
$=-3\left(x - \dfrac{1}{3}\right)^{2}-\dfrac{2}{3}$
(3)解:$y=ax^{2}+bx + c$
$=a\left(x^{2}+\dfrac{b}{a}x\right)+c$
$=a\left(x^{2}+\dfrac{b}{a}x+\dfrac{b^{2}}{4a^{2}}-\dfrac{b^{2}}{4a^{2}}\right)+c$
$=a\left[\left(x + \dfrac{b}{2a}\right)^{2}-\dfrac{b^{2}}{4a^{2}}\right]+c$
$=a\left(x + \dfrac{b}{2a}\right)^{2}-\dfrac{b^{2}}{4a}+c$
$=a\left(x + \dfrac{b}{2a}\right)^{2}+\dfrac{4ac - b^{2}}{4a}$
(1)解:$y=x^{2}-8x+10$
$=x^{2}-8x+16 - 16 + 10$
$=(x - 4)^{2}-6$
(2)解:$y=-3x^{2}+2x - 1$
$=-3\left(x^{2}-\dfrac{2}{3}x\right)-1$
$=-3\left(x^{2}-\dfrac{2}{3}x+\dfrac{1}{9}-\dfrac{1}{9}\right)-1$
$=-3\left[\left(x - \dfrac{1}{3}\right)^{2}-\dfrac{1}{9}\right]-1$
$=-3\left(x - \dfrac{1}{3}\right)^{2}+\dfrac{1}{3}-1$
$=-3\left(x - \dfrac{1}{3}\right)^{2}-\dfrac{2}{3}$
(3)解:$y=ax^{2}+bx + c$
$=a\left(x^{2}+\dfrac{b}{a}x\right)+c$
$=a\left(x^{2}+\dfrac{b}{a}x+\dfrac{b^{2}}{4a^{2}}-\dfrac{b^{2}}{4a^{2}}\right)+c$
$=a\left[\left(x + \dfrac{b}{2a}\right)^{2}-\dfrac{b^{2}}{4a^{2}}\right]+c$
$=a\left(x + \dfrac{b}{2a}\right)^{2}-\dfrac{b^{2}}{4a}+c$
$=a\left(x + \dfrac{b}{2a}\right)^{2}+\dfrac{4ac - b^{2}}{4a}$
查看更多完整答案,请扫码查看


