《2025年新课程课堂同步练习册九年级数学上册人教版》

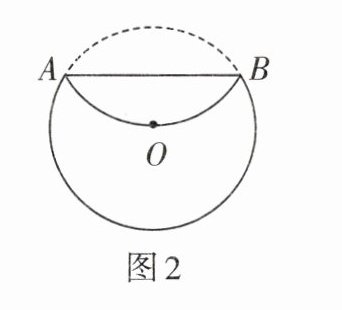
2. 如图2,将半径为4 cm的圆形纸片折叠后,圆弧恰好经过圆心O,则$\widehat{AB}$的长度为$\frac{8π}{3}$cm.

答案： 解：过点O作OD⊥AB，交AB于点D，交$\widehat{AB}$于点C，连接OA、OB。
由折叠性质知OD=DC，又OA=OC=4cm，故OD=$\frac{1}{2}$OC=2cm。
在Rt△OAD中，OA=4cm，OD=2cm，
∴cos∠AOD=$\frac{OD}{OA}$=$\frac{2}{4}$=$\frac{1}{2}$，
∴∠AOD=60°，同理∠BOD=60°，
∴∠AOB=∠AOD+∠BOD=120°=$\frac{2π}{3}$rad。
$\widehat{AB}$的长=$\frac{nπr}{180}$=$\frac{120×π×4}{180}$=$\frac{8π}{3}$cm。
$\frac{8π}{3}$

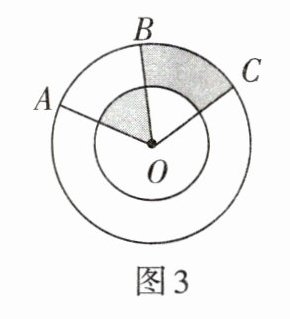
3. 如图3,两个同心圆中,大圆的半径OA= 4 cm,∠AOB= ∠BOC= 60°,则图中阴影部分的面积是$$$\frac 8 3π$$$cm^2.

答案： $\frac 8 3π$

4. 已知一条弧长为20π,它所对的圆心角为150°,则这条弧所在圆的半径为24.

答案： 解：设这条弧所在圆的半径为$r$。
根据弧长公式$l = \frac{n\pi r}{180}$（其中$l$为弧长，$n$为圆心角度数，$r$为半径），已知$l = 20\pi$，$n = 150^\circ$，可得：
$20\pi = \frac{150\pi r}{180}$
化简得：$20\pi = \frac{5\pi r}{6}$
两边同时除以$\pi$：$20 = \frac{5r}{6}$
解得：$r = 24$
24

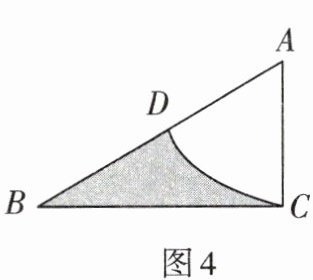
5. 如图4,已知Rt△ABC中,∠C= 90°,∠B= 30°,BC= 4$\sqrt{3}$,以A点为圆心,AC长为半径作$\widehat{DC}$,∠B与$\widehat{DC}$围成的阴影部分的面积为$8\sqrt {3}-\frac 8 3π$(结果用含π的代数式表示).

答案： $8\sqrt {3}-\frac 8 3π$

1. 如图5,已知扇形AOB的半径为10,∠AOB= 60°,求$\widehat{AB}$的长(结果保留π).

答案： 解：已知扇形AOB的半径$r = 10$，圆心角$\angle AOB = 60^\circ$。
根据弧长公式$l=\frac{n\pi r}{180}$（其中$n$为圆心角度数，$r$为半径），可得：
$\widehat{AB}$的长$l=\frac{60\pi×10}{180}=\frac{600\pi}{180}=\frac{10\pi}{3}$
答：$\widehat{AB}$的长为$\frac{10\pi}{3}$。

2. 砖雕是一种历史悠久的古建筑装饰艺术,是第一批国家级非物质文化遗产. 如图6是一块扇面形的砖雕作品,它的部分设计图如图7所示,其中扇形OBC和扇形OAD有相同的圆心O,且圆心角∠O= 100°,若OA= 120 cm,OB= 60 cm,则图7中阴影部分的面积是多少(结果保留π)?

答案： 解：
阴影部分的面积 $S_{阴影} = S_{扇形OAD} - S_{扇形OBC}$
$= \frac{100\pi × 120^2}{360} - \frac{100\pi × 60^2}{360}$
$= \frac{100\pi × 14400}{360} - \frac{100\pi × 3600}{360}$
$= 4000\pi - 1000\pi$
$= 3000\pi (cm^2)$
答：阴影部分的面积是 $3000\pi cm^2$。