《2025年新课程课堂同步练习册九年级数学上册人教版》

1. 指出下列二次函数的二次项系数、一次项系数和常数项.

答案：

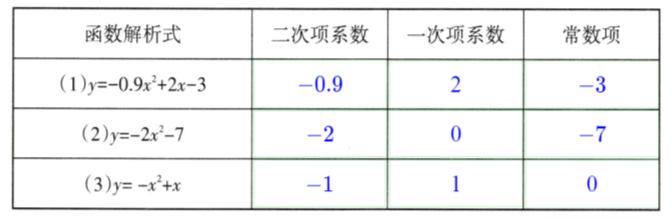
2. 一个长方形的长是宽的3倍,设长方形的宽为$ x $(单位:cm),写出面积$ y $(单位:cm^2)与$ x $之间的关系式.

答案： 解：根据题意，长方形的长为$3x$ cm，宽为$x$ cm。
所以，面积 $y = 长 × 宽 = 3x × x = 3x^{2}$。
即，面积$y$与宽$x$的关系式为：$y = 3x^{2}$。

3. 已知函数$ y= (a-1)x^{2}+4x-3 $($ a $为常数).
(1)当$ a $取何值时,此函数为一次函数?
(2)当$ a $取何值时,此函数为二次函数? 你能分别说出二次项系数、一次项系数和常数项吗?

答案：
(1) 解：
为了使函数 $y = (a-1)x^{2} + 4x - 3$ 成为一次函数，需要 $a-1 = 0$。
解得 $a = 1$。

∴ 当 $a = 1$ 时，此函数为一次函数。
(2) 解：
为了使函数 $y = (a-1)x^{2} + 4x - 3$ 成为二次函数，需要 $a-1 \neq 0$。
解得 $a \neq 1$。
二次项系数为 $a-1$，一次项系数为 $4$，常数项为 $-3$。

∴ 当 $a \neq 1$ 时，此函数为二次函数，且二次项系数为 $a-1$，一次项系数为 $4$，常数项为 $-3$。

4. 学校准备将一块长20 m,宽14 m的矩形绿地扩建,如果长和宽都增加$ x $ m,设增加的面积是$ y $ m^2.
(1)求$ y 与 x $之间的函数表达式；
(2)若要使绿地面积增加72 m^2,则长与宽都要增加多少米?

答案：
(1) 解：原绿地面积为 $20 × 14 = 280 \, m^2$，扩建后长为 $(20 + x) \, m$，宽为 $(14 + x) \, m$，面积为 $(20 + x)(14 + x)$。
增加的面积 $y = (20 + x)(14 + x) - 280$，
展开得 $y = x^2 + 34x + 280 - 280$，
即 $y = x^2 + 34x$。
(2) 解：由题意得 $x^2 + 34x = 72$，
整理得 $x^2 + 34x - 72 = 0$，
因式分解 $(x + 36)(x - 2) = 0$，
解得 $x_1 = -36$（舍去），$x_2 = 2$。
答：长与宽都要增加2米。