《2025年新课程课堂同步练习册九年级数学上册人教版》

2. 《九章算术》被尊为古代数学“群经之首”,其卷九勾股篇记载:今有圆材埋于壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何? 大意是,如图7,今有一圆柱形木材,其部分埋在了墙壁中,不知其大小,用锯去锯这木材,锯口深CD等于1寸,弦AB长1尺,问圆形木材的直径是多少?(1尺= 10寸)

答案： 圆形木材的直径是$26$寸（或$2$尺$6$寸 ）。

3. 如图8,在平面直角坐标系中,点A的坐标是(20,0),点B的坐标是(16,0),点C,D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,求点C的坐标.

答案：

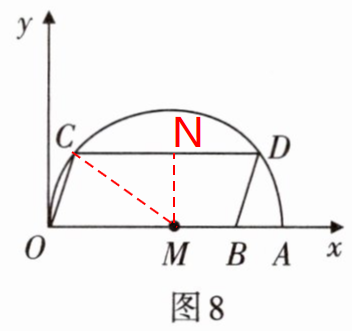
解：过点M作MN⊥CD于点N，连接CM，如图所示
∵A(20，0)
∴M(10，0)
∴OM=CM=10
∵四边形OCDB是平行四边形，B(16，0)
∴CD=OB=16
∵MN⊥CD
∴N是CD的中点，$CN=\frac 1 2CD=8$
∴$MN=\sqrt {{CM}^2-{CN}^2}=\sqrt {{10}^2-{8}^2}=6$
∴C(2，6)

1. 如果两个圆心角相等,那么(D)
A.这两个圆心角所对的弦相等
B.这两个圆心角所对的弧相等
C.这两个圆心角所对的弦的弦心距相等
D.以上说法都不对

答案： D

2. 如图1,⊙O中,如果$\widehat{AB}= 2\widehat{AC}$,那么(C)

A.AB= AC
B.AB= 2AC
C.AB＜2AC
D.AB＞2AC

答案： C.$AB＜2AC$。