第70页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. 过$\odot O$外一点P,可以作(
A.0
B.1
C.2
D.1或2
C
)条$\odot O$的切线.A.0
B.1
C.2
D.1或2
答案:
C. 2。
2. 已知$\triangle ABC$的内心为点I,那么I是$\triangle ABC$的(
A.三条中线的交点
B.三条高的交点
C.三条角平分线的交点
D.三条边的垂直平分线的交点
C
)A.三条中线的交点
B.三条高的交点
C.三条角平分线的交点
D.三条边的垂直平分线的交点
答案:
C
3. 下列四边形中一定有内切圆的是(
A.直角梯形
B.等腰梯形
C.矩形
D.菱形
BD
)A.直角梯形
B.等腰梯形
C.矩形
D.菱形
答案:
BD
4. 如图1,从$\odot O$外一点P引$\odot O$的两条切线PA,PB,切点分别为A,B. 如果$\angle APB= 60^{\circ },PA= 8$,那么弦AB的长是(

A.4
B.8
C.$4\sqrt{3}$
D.$8\sqrt{3}$
B
)
A.4
B.8
C.$4\sqrt{3}$
D.$8\sqrt{3}$
答案:
B
5. 一根钢管放在V形架内,图2是其截面图,O为钢管的圆心. 若钢管的半径为25 cm,$\angle MPN= 60^{\circ }$,则OP的长为(
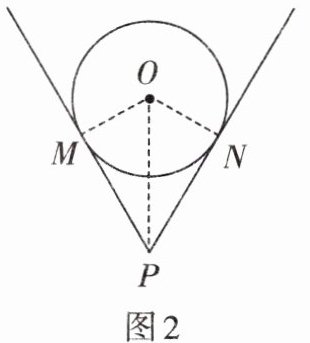
A.50 cm
B.$25\sqrt{3}$ cm
C.$\frac{50\sqrt{3}}{3}$ cm
D.$50\sqrt{3}$ cm
A
)
A.50 cm
B.$25\sqrt{3}$ cm
C.$\frac{50\sqrt{3}}{3}$ cm
D.$50\sqrt{3}$ cm
答案:
A
1. 如图3,已知I为$\triangle ABC$的内心,$\angle B= 50^{\circ }$,则$\angle AIC= $

115
度.
答案:
115
2. 如图4,直线AB,BC,CD分别与$\odot O$相切于E,F,G,且$AB// CD$,若$OB= 6\ cm,OC= 8\ cm$,则$\angle BOC= $
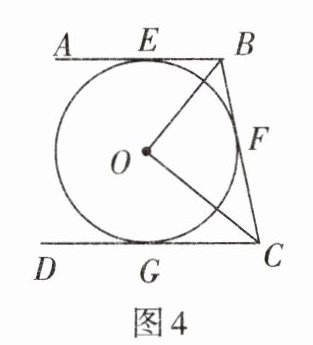
90
度,$BE+CG= $10cm
.
答案:
90
10cm
10cm
3. 等边三角形内切圆半径与外接圆半径之比是
1∶2
.
答案:
1∶2
4. 如图5,PA,PB分别切$\odot O$于点A,B,点E是$\odot O$上一点,且$\angle AEB= 60^{\circ }$,则$\angle P= $

60
度.
答案:
60
5. 如图6,边长为a的正三角形的内切圆半径是
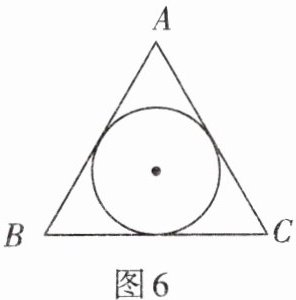
$\frac{\sqrt{3}}{6}a$
.
答案:
【解析】:本题考查正三角形与内切圆的关系,可通过连接正三角形的顶点、内切圆的圆心以及切点,构造直角三角形,利用正三角形的性质和直角三角形的边角关系来求解内切圆半径。
步骤一:连接正三角形的顶点$A$、内切圆的圆心$O$以及边$AB$的切点$E$,则$OE\perp AB$(圆的切线性质:圆的切线垂直于经过切点的半径),$OA$平分$\angle BAC$(正三角形的内心、外心、重心、垂心四心合一,$O$为正三角形的内心,所以$OA$平分$\angle BAC$)。
步骤二:因为$\triangle ABC$是正三角形,所以$\angle BAC = 60^{\circ}$,那么$\angle OAE = \frac{1}{2}\angle BAC = 30^{\circ}$。
步骤三:在$Rt\triangle AOE$中,$AE=\frac{1}{2}AB$(等腰三角形三线合一,$OE\perp AB$,$O$在$AC$的角平分线上,所以$E$为$AB$中点),已知正三角形边长为$a$,则$AE = \frac{a}{2}$。
步骤四:设内切圆半径$OE = r$,根据直角三角形中$30^{\circ}$所对的直角边等于斜边的一半,可得$AO = 2r$。
步骤五:再根据勾股定理$AO^{2}=OE^{2}+AE^{2}$,即$(2r)^{2}=r^{2}+(\frac{a}{2})^{2}$。
步骤六:解方程$(2r)^{2}=r^{2}+(\frac{a}{2})^{2}$:
$\begin{aligned}4r^{2}&=r^{2}+\frac{a^{2}}{4}\\4r^{2}-r^{2}&=\frac{a^{2}}{4}\\3r^{2}&=\frac{a^{2}}{4}\\r^{2}&=\frac{a^{2}}{12}\\r&=\frac{\sqrt{3}}{6}a\end{aligned}$
【答案】:$\frac{\sqrt{3}}{6}a$
步骤一:连接正三角形的顶点$A$、内切圆的圆心$O$以及边$AB$的切点$E$,则$OE\perp AB$(圆的切线性质:圆的切线垂直于经过切点的半径),$OA$平分$\angle BAC$(正三角形的内心、外心、重心、垂心四心合一,$O$为正三角形的内心,所以$OA$平分$\angle BAC$)。
步骤二:因为$\triangle ABC$是正三角形,所以$\angle BAC = 60^{\circ}$,那么$\angle OAE = \frac{1}{2}\angle BAC = 30^{\circ}$。
步骤三:在$Rt\triangle AOE$中,$AE=\frac{1}{2}AB$(等腰三角形三线合一,$OE\perp AB$,$O$在$AC$的角平分线上,所以$E$为$AB$中点),已知正三角形边长为$a$,则$AE = \frac{a}{2}$。
步骤四:设内切圆半径$OE = r$,根据直角三角形中$30^{\circ}$所对的直角边等于斜边的一半,可得$AO = 2r$。
步骤五:再根据勾股定理$AO^{2}=OE^{2}+AE^{2}$,即$(2r)^{2}=r^{2}+(\frac{a}{2})^{2}$。
步骤六:解方程$(2r)^{2}=r^{2}+(\frac{a}{2})^{2}$:
$\begin{aligned}4r^{2}&=r^{2}+\frac{a^{2}}{4}\\4r^{2}-r^{2}&=\frac{a^{2}}{4}\\3r^{2}&=\frac{a^{2}}{4}\\r^{2}&=\frac{a^{2}}{12}\\r&=\frac{\sqrt{3}}{6}a\end{aligned}$
【答案】:$\frac{\sqrt{3}}{6}a$
查看更多完整答案,请扫码查看


