《2025年通成学典课时作业本七年级数学上册苏科版苏州专版》

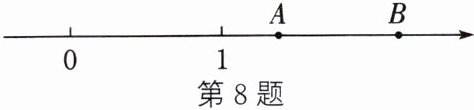
8. 如图,数轴上的点A,B分别表示数a,b,则$\frac {1}{a}$＞$\frac {1}{b}$(填“＞”“＜”或“=”).

答案： $＞$

9. 先运用乘法运算律将下列算式变形,再计算出结果.
(1)$8×(-5.06)×1.25=$$8 × 1.25 × (-5.06)$=$-50.6$;
(2)$(\frac {7}{12}-\frac {4}{15}-\frac {3}{4})×(-60)=$$\frac{7}{12} × (-60) + (-\frac{4}{15}) × (-60) + (-\frac{3}{4}) × (-60)$=$26$;
(3)$\frac {4}{5}×(-\frac {5}{13})-(-\frac {3}{5})×(-\frac {5}{13})+\frac {5}{13}×1\frac {3}{5}=$$[\frac{4}{5} - (-\frac{3}{5}) + (-1\frac{3}{5})] × (-\frac{5}{13})$=$\frac{1}{13}$.

答案：
(1) $8 × 1.25 × (-5.06)$ $-50.6$
(2) $\frac{7}{12} × (-60) + (-\frac{4}{15}) × (-60) + (-\frac{3}{4}) × (-60)$ $26$
(3) $[\frac{4}{5} - (-\frac{3}{5}) + (-1\frac{3}{5})] × (-\frac{5}{13})$ $\frac{1}{13}$

10. 计算:
(1)$(-4)×(-18.36)×2.5$;
(2)$(-\frac {3}{7})×0.125×(-2\frac {1}{3})×(-8)$;
(3)$(-99\frac {71}{72})×36$;
(4)$4×(-\frac {1}{2}+\frac {1}{3}-\frac {1}{4}-\frac {1}{5})×(-5)$;
(5)$(-354)×(-3)+(-354)×5-(-2)×354$.

答案：
(1) $183.6$
(2) $-1$
(3) $-3599\frac{1}{2}$
(4) $\frac{37}{3}$ 解析：先利用乘法交换律，再利用乘法分配律，此时原式$= (-20) × (-\frac{1}{2} + \frac{1}{3} - \frac{1}{4} - \frac{1}{5}) = 10 - \frac{20}{3} + 5 + 4 = 19 - \frac{20}{3} = \frac{57}{3} - \frac{20}{3} = \frac{37}{3}$。
(5) $0$

11. (新考法·新定义题)定义一种新的运算:$x★y= (x+2)×(y+2)$,等式右侧是通常的混合运算.
(1) 计算$(-3)★(-4)与(-4)★(-3)$,此运算满足交换律吗?
(2) 计算$[(-3)★(-4)]★(-5)与(-3)★[(-4)★(-5)]$,此运算满足结合律吗?

答案：
(1) 因为$(-3) \star (-4) = [(-3) + 2] × [(-4) + 2] = (-1) × (-2) = 2$，$(-4) \star (-3) = [(-4) + 2] × [(-3) + 2] = (-2) × (-1) = 2$，$2 = 2$，所以满足交换律
(2) 因为$[(-3) \star (-4)] \star (-5) = 2 \star (-5) = (2 + 2) × [(-5) + 2] = 4 × (-3) = -12$，又因为$(-4) \star (-5) = [(-4) + 2] × [(-5) + 2] = (-2) × (-3) = 6$，则$(-3) \star 6 = [(-3) + 2] × (6 + 2) = (-1) × 8 = -8$，$-12 \neq -8$，所以不满足结合律