《2025年通成学典课时作业本七年级数学上册苏科版苏州专版》

16. (2024·北京)为防治污染,保护和改善生态环境,自$2023年7月1$日起,我国全面实施汽车国六排放标准$6b$阶段(以下简称“标准”).对某型号汽车,“标准”要求$A类物质排放量不超过35mg/km$,$A$,$B两类物质排放量之和不超过50mg/km$.已知该型号某汽车的$A$,$B两类物质排放量之和原为92mg/km$.经过一次技术改进,该汽车的$A类物质排放量降低了50\%$,$B类物质排放量降低了75\%$,$A$,$B两类物质排放量之和为40mg/km$.判断这次技术改进后该汽车的$A$类物质排放量是否符合“标准”,并说明理由.

答案： 这次技术改进后该汽车的 A 类物质排放量符合“标准”理由：设原来该汽车的 A 类物质排放量为 $ x $ mg/km，则该汽车的 B 类物质排放量为 $ (92 - x) $ mg/km。根据题意，得 $ (1 - 50\%)x + (1 - 75\%)(92 - x) = 40 $。解这个方程，得 $ x = 68 $，此时 $ (1 - 50\%)x = 34 $，即这次技术改进后该汽车的 A 类物质排放量为 34 mg/km。因为 $ 34 $ mg/km $ ＜ 35 $ mg/km，所以这次技术改进后该汽车的 A 类物质排放量符合“标准”。

17. 若关于$x的方程5x - a = 0的解比关于y的方程3y + a = 0的解小2$,则$a$的值是(B)
A.$\frac{15}{4}$
B.$-\frac{15}{4}$
C.$\frac{4}{15}$
D.$-\frac{4}{15}$

答案： B

18. (2024·广州)定义新运算：$a\otimes b= \begin{cases}a^{2}-b,a\leqslant0,\\-a + b,a＞0.\end{cases} $例如：$(-2)\otimes4= (-2)^{2}-4 = 0$,$2\otimes3= -2 + 3 = 1$.若$x\otimes1= -\frac{3}{4}$,则$x$的值为(D)
A.$\pm\frac{1}{2}$
B.$\frac{7}{4}$
C.$\pm\frac{1}{2}或\frac{7}{4}$
D.$-\frac{1}{2}或\frac{7}{4}$

答案： D 解析：因为 $ x\otimes 1 = -\frac{3}{4} $，所以当 $ x ≤ 0 $ 时，$ x^2 - 1 = -\frac{3}{4} $，即 $ x^2 = \frac{1}{4} $，易得 $ x = \frac{1}{2} $（不合题意，舍去）或 $ x = -\frac{1}{2} $；当 $ x ＞ 0 $ 时，$ -x + 1 = -\frac{3}{4} $，解得 $ x = \frac{7}{4} $。综上所述，\$ x $ 的值为 $ -\frac{1}{2} $ 或 $ \frac{7}{4} $。

19. (方程思想)任何一个无限循环小数都可以写成分数的形式,应该怎样写呢？我们以无限循环小数$0.\dot{7}$为例进行说明：设$0.\dot{7}= x$.由$0.\dot{7}= 0.7777…$可知,$10x = 7.7777…$.所以$10x - x = 7$,解得$x= \frac{7}{9}$.于是,得$0.\dot{7}= \frac{7}{9}$.将$0.\dot{3}\dot{6}$写成分数的形式为$\frac{4}{11}$.

答案： $\frac{4}{11}$

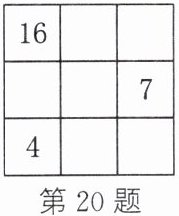
20. (2023·德阳)在初中数学文化节游园活动中,被称为“数学小王子”的小明参加了“智取九宫格”游戏比赛,活动规则是：在九宫格中,除了已经填写的三个数之外的每一个方格中,填入一个数,使每一横行、每一竖列以及两条对角线上的$3$个数之和分别相等,且均为$m$.小明抽取到的题目如图所示,他运用初中所学的数学知识,很快就完成了这个游戏,则$m$的值为______.

39

答案： 39 解析：设九宫格中最中间的数为 $ x $。根据第 1 列的中间的数与第 2 行的最左侧的数重合，得 $ 16 + 4 = 7 + x $，解得 $ x = 13 $。由于九宫格每一横行、每一竖列以及两条对角线上的 3 个数之和等于最中间数的 3 倍，所以 $ m = 3x = 39 $。

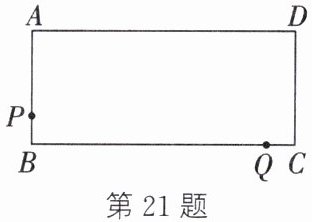
21. (分类讨论思想)(2025·常熟期末)如图,在长方形$ABCD$中,$AB = 6$,$BC = 14$,动点$P从点A出发以每秒3个单位长度的速度沿A→B→C向终点C$匀速运动,动点$Q从点C出发以每秒1个单位长度的速度沿CB向终点B$匀速运动.若点$P$,$Q$同时出发,当一个动点到达终点时,另一个动点也同时停止运动.设两点运动的时间为$t$秒,当$PB = 2CQ$时,$t$的值为$\frac{6}{5}$或6.

答案： $\frac{6}{5}$ 或 6 解析：当点 $ P $ 在 $ AB $ 上时，$ BP = 6 - 3t,CQ = t $。由 $ PB = 2CQ $，得 $ 2t = 6 - 3t $，解得 $ t = \frac{6}{5} $；当点 $ P $ 在 $ BC $ 上时，$ PB = 3t - 6,CQ = t $。由 $ PB = 2CQ $，得 $ 2t = 3t - 6 $，解得 $ t = 6 $。综上所述，$ t = \frac{6}{5} $ 或 6。