第109页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
8. 如图所示为一个几何体的侧面展开图,则该几何体是 (
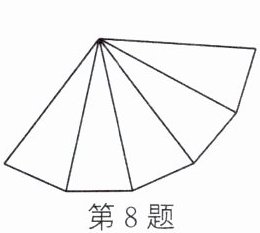
A.三棱柱
B.三棱锥
C.五棱柱
D.五棱锥
D
)
A.三棱柱
B.三棱锥
C.五棱柱
D.五棱锥
答案:
D
9. (2024·济宁)如图是一个正方体的展开图,把展开图折叠成正方体后,有“建”字一面的相对面上的字是 (
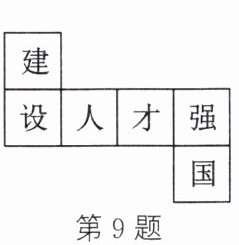
A.人
B.才
C.强
D.国
D
)
A.人
B.才
C.强
D.国
答案:
D
10. 如图所示为一个正方体纸盒的表面展开图. 若纸盒中相对两个面上的数互为倒数,则代数式 $ a - bc $ 的值为
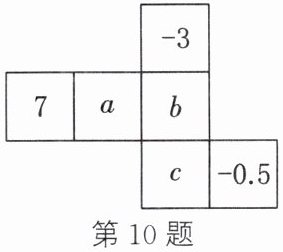
$-1\frac {20}{21}$
.
答案:
$-1\frac {20}{21}$ 解析:根据题意,得$a=-2,b=\frac {1}{7},c=-\frac {1}{3}$,所以$a-bc=-2-\frac {1}{7}×(-\frac {1}{3})=-1\frac {20}{21}.$
11. (2024·江西)如图所示为 4×3 的正方形网格,选择一空白小正方形,能与涂色部分组成正方体表面展开图的方法有

2
种.
答案:
2
12. (新情境·游戏活动)用边长为 1 的正方形纸片(如图①)剪出一副“七巧板”,并将其拼成如图②所示的“小天鹅”,则涂色部分的面积是原正方形纸片面积的 (
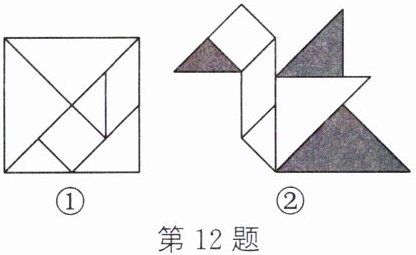
A.$ \frac{1}{2} $
B.$ \frac{3}{8} $
C.$ \frac{7}{16} $
D.$ \frac{9}{16} $
C
)
A.$ \frac{1}{2} $
B.$ \frac{3}{8} $
C.$ \frac{7}{16} $
D.$ \frac{9}{16} $
答案:
C
13. 如图,正方体的六个面上标着连续的整数. 若相对的两个面上所标数的和相等,则这六个数的和为
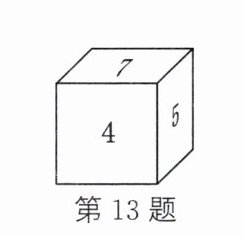
39
.
答案:
39
14. (2023·青岛)一个不透明小立方块的六个面上分别标有数字 1,2,3,4,5,6,其展开图如图①所示. 在一张不透明的桌子上,按如图②所示的方式将三个这样的小立方块搭成一个几何体,则该几何体能看得到的面上数字之和最小为______.
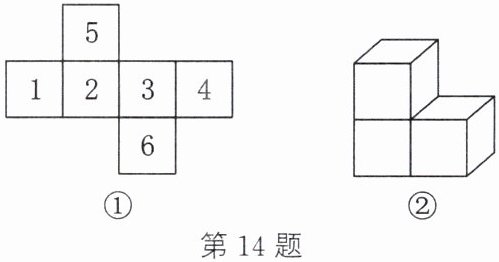

32
答案:
32 解析:由正方体的表面展开图的“相间、Z端是对面”可知,“1”与“3”、“2”与“4”、“5”与“6”是对面. 因此要使题图②中几何体能看得到的面上数字之和最小,最右边的那个正方体所能看到的4个面上的数字为1,2,3,5,最上端的那个正方体所能看到的5个面上的数字为1,2,3,4,5,左下角的那个正方体所能看到的3个面上的数字为1,2,3. 所以该几何体能看得到的面上数字之和最小为$11+15+6=32.$
15. (新考法·探究题)用若干灰、白两色的小正方形按如图所示的方式摆放,依此规律,第 $ n $ 个图形中小正方形的总个数为
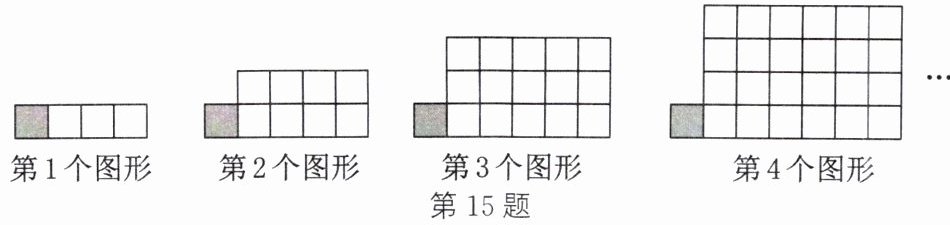
$(n+1)^{2}$
;若第 $ n $ 个图形中白色小正方形的个数记为 $ S_n $, 计算 $ \left(1+\frac{1}{S_1}\right) × \left(1+\frac{1}{S_2}\right) × \left(1+\frac{1}{S_3}\right) × … × \left(1+\frac{1}{S_{20}}\right) $ 的结果为$\frac {21}{11}$
.
答案:
$(n+1)^{2}$ $\frac {21}{11}$ 解析:解答第2空时,先根据前4个图形找出第n个图形的规律:$S_{n}=n(n+2)$,则$1+\frac {1}{S_{n}}=\frac {(n+1)^{2}}{n(n+2)}$,所以原式$=\frac {2×2}{1×3}×\frac {3×3}{2×4}×\frac {4×4}{3×5}×... ×\frac {21×21}{20×22}=\frac {2×21}{22}=\frac {21}{11}.$
查看更多完整答案,请扫码查看


