《2025年学霸提优大试卷八年级数学上册苏科版》

8. 如图,在 $ \mathrm{Rt} \triangle ABC $ 中, $ \angle BAC= 90^{\circ}, CD $ 是 $ \triangle ABC $ 的角平分线, $ AE \perp CD $ 于点 $ E $, 连接 $ BE,AB= 6,AC= 8,BC= 10 $, 则 $ \triangle ABE $ 的面积是 ( )


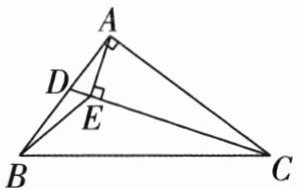
A.$ \frac{9}{5} $
B.2
C.$ \frac{12}{5} $
D.$ \frac{24}{5} $

答案：
C　　[解析]如图,过点A作AH⊥BC于H,延长AE交BC于F,在Rt△ABC中,∠BAC = 90°,AB = 6,AC = 8,BC = 10,
∵S△ABC = $\frac{1}{2}$BC·AH = $\frac{1}{2}$AB·AC,
∴AH = $\frac{AB·AC}{BC}$ = $\frac{6×8}{10}$ = $\frac{24}{5}$.
∵CD是△ABC的角平分线,
∴∠ACE = ∠FCE.
∵AE⊥CD,
∴∠AEC = ∠FEC = 90°.在△ACE和△FCE中,{∠ACE = ∠FCE,CE = CE,∠AEC = ∠FEC = 90°,
∴△ACE≌△FCE(ASA),
∴AC = CF = 8,AE = FE,
∴BF = BC - CF = 2,
∴S△ABF = $\frac{1}{2}$BF·AH = $\frac{1}{2}$×2×$\frac{24}{5}$ = $\frac{24}{5}$.
∵AE = FE,
∴S△ABE = S△BEF = $\frac{1}{2}$S△ABF = $\frac{1}{2}$×$\frac{24}{5}$ = $\frac{12}{5}$.故选C.
　　　　　　　　　　　　　　　　　　

9. 如果 $ a,b,c $ 为一个三角形的三边, 且 $ (a-b)^2+(a-c)^2+|b-c|= 0 $, 那么这是一个等边三角形.

答案： 等边　　[解析]
∵(a - b)²+(a - c)²+|b - c| = 0,
∴a - b = 0,a - c = 0,b - c = 0,
∴a = b,a = c,b = c,
∴a = b = c,
∴这个三角形是等边三角形

10. 已知等腰三角形的一个外角为 $ 108^{\circ} $, 则其底角的度数为54°或72°.

答案： 54°或72°　　[解析]
∵等腰三角形的一个外角为108°,
∴与这个外角相邻的内角是180° - 108° = 72°.①72°角是顶角时,底角为$\frac{1}{2}$×(180° - 72°) = 54°;②72°角是底角时,底角为72°,综上所述，其底角的度数为54°或72°.

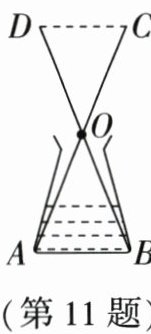
11. 数学课上老师布置了“测量锥形瓶内部底面的直径”的探究任务, 小聪想到老师讲过“利用全等三角形对应边相等, 可以把不能直接测量的物体‘移’到可以直接测量的位置测量”于是他设计了如下方案: 如图, 用螺丝钉将两根小棒 $ AC,BD $ 的中点 $ O $ 固定, 测得 $ CD= 8 \mathrm{~cm} $, 就可知道内径 $ AB $ 的长度是8cm.

答案： 8cm　　[解析]在△COD和△AOB中,{OC = OA,∠COD = ∠AOB,OD = OB,
∴△COD≌△AOB(SAS),
∴AB = CD = 8cm.

12. 如图, 在 $ \triangle ABC $ 中, $ DE,FG $ 分别是边 $ AB,AC $ 的垂直平分线, 分别交 $ BC $ 于 $ E,G $ 两点, 连接 $ AE,AG $, 若 $ BC= 8 $, 则 $ \triangle AEG $ 的周长为8.

答案： 8　　[解析]
∵DE,FG分别是边AB,AC的垂直平分线，
∴AE = BE,AG = CG,
∴BC = BE + EG + CG = AE + EG + AG,
∴△AEG的周长 = AE + EG + AG = BC = 8.

13. 如图,已知 $ \triangle ABC \cong \triangle EDF $, 点 $ F,A,D $ 在同一条直线上, $ AD $ 是 $ \angle BAC $ 的平分线, $ \angle EDA= 20^{\circ} $, $ \angle F= 60^{\circ} $, 则 $ \angle DAC $ 的度数是50°.

答案： 50°　　[解析]
∵△ABC≌△EDF,
∴∠B = ∠EDF,∠C = ∠F;
∵∠EDA = 20°,∠F = 60°,
∴∠B = 20°,∠C = 60°,
∴∠BAC = 180° - ∠B - ∠C = 100°.
∵AD是∠BAC的平分线,
∴∠DAC = $\frac{1}{2}$∠BAC = 50°.

14. 如图, 在 $ \triangle ABC $ 中, $ \angle ACB= 90^{\circ}, D $ 在 $ BC $ 上, $ E $ 是 $ AB $ 的中点, $ AD,CE $ 相交于 $ F $, 且 $ AD= DB $. 若 $ \angle B= 20^{\circ} $, 则 $ \angle DFE $ 等于60°.

答案： 60°　　[解析]
∵在△ABC中,∠ACB = 90°,E是AB的中点,
∴BE = CE.
∵∠B = 20°,
∴∠ECB = ∠B = 20°.
∵AD = BD,∠B = 20°,
∴∠DAB = ∠B = 20°,
∴∠ADC = ∠B + ∠DAB = 20° + 20° = 40°,
∴∠DFE = ∠ADC + ∠ECB = 40° + 20° = 60°.

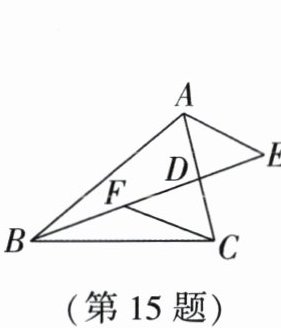
15. 如图,已知 $ BD $ 是 $ \triangle ABC $ 的中线, $ CF $ 是 $ \triangle BCD $ 的中线, $ AE // CF $ 交 $ BD $ 的延长线于点 $ E $. 若 $ \triangle ADE $ 的面积为 3, 则 $ \triangle ABC $ 的面积是______12.

答案： 12　　[解析]
∵BD是△ABC的中线,
∴CD = AD.
∵AE//CF,△ADE的面积为3,
∴∠DFC = ∠E.在△CDF和△ADE中,{∠CDF = ∠ADE,∠DFC = ∠E,CD = AD,
∴△CDF≌△ADE(AAS),
∴S△CDF = S△ADE = 3.
∵CF是△BCD的中线,
∴BF = DF,
∴S△CBF = S△CDF = 3,
∴S△ABD = S△CBD = 2S△CDF = 6,
∴S△ABC = 2S△ABD = 12.

16. (2024·无锡期中)如图, $ CB \perp AD,AE \perp CD $, 垂足分别为点 $ B,E,AE,BC $ 相交于点 $ F $, 若 $ AB= BC= 16,CF= 8 $, 连接 $ DF $, 则图中阴影部分的面积为______.

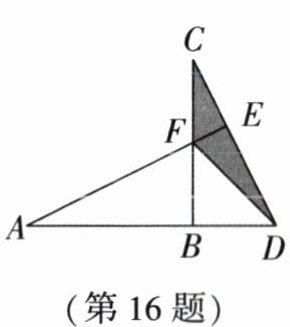
32

答案： 32　　[解析]
∵CB⊥AD,AE⊥CD,
∴∠ABF = ∠CBD = 90°,∠FEC = 90°.
∵∠AFB = ∠EFC,
∴∠A = ∠C.在△ABF和△CBD中,{∠ABF = ∠CBD,AB = CB,∠A = ∠C,
∴△ABF≌△CBD(ASA),
∴BF = BD.
∵BF = BC - CF = 16 - 8 = 8,
∴BD = 8,
∴图中阴影部分面积 = $\frac{1}{2}$FC·BD = $\frac{1}{2}$×8×8 = 32.

17. 已知 $ \triangle ABC, \angle BAC= 30^{\circ}, AB= 6 $, 要使满足条件的 $ \triangle ABC $ 唯一确定, 那么 $ BC $ 边长度 $ x $ 的取值范围为______.

答案：
x = 3或x≥6　　[解析]如图,过B点作BD⊥AC于点D,则△ABD是含30°角的直角三角形.再延长AD到E点，使DE = AD.①当C点和D点重合时,△ABC是含30°角的直角三角形,BC = $\frac{1}{2}$AB = 3,这个三角形是唯一的;②当C点和E点重合时,△ABC是等腰三角形,BC = AB = 6,这个三角形也是唯一的;③当C点在线段AE的延长线上时,即x大于BE,也就是x＞6,这时,三角形ABC也是唯一的.综上所述，∠BAC = 30°,AB = 6,要使△ABC唯一确定,那么BC的长度x满足的条件是x = 3或x≥6.
　　　　

18. 如图, 在 $ \triangle ABC $ 中, $ D $ 为 $ AB $ 中点, $ DE \perp AB, \angle ACE+\angle BCE= 180^{\circ}, EF \perp BC $ 交 $ BC $ 于 $ F,AC= 8,BC= 12 $, 则 $ BF $ 的长为______.

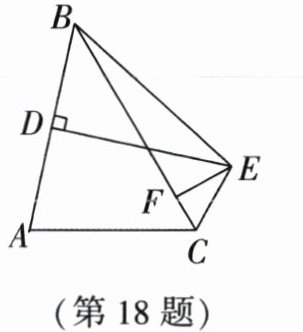
答案：
10　　[解析]连接AE,过点E作EG⊥AC交AC的延长线于点G，
∵D为AB中点,DE⊥AB,
∴EA = EB.
∵∠ACE + ∠BCE = 180°,∠ACE + ∠ECG = 180°,
∴∠ECG = ∠BCE.
∵EF⊥BC,EG⊥AC,
∴EG = EF.在Rt△EFC和Rt△EGC中,{EF = EG,EC = EC,
∴Rt△EFC≌Rt△EGC(HL),
∴CF = CG.同理可得BF = AG,
∴12 - CF = 8 + CF,解得CF = 2,
∴BF = 12 - 2 = 10.