《2025年学霸提优大试卷八年级数学上册苏科版》

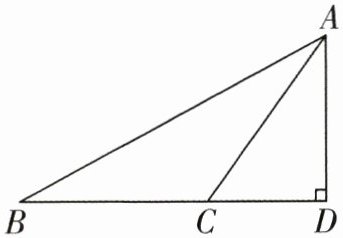
21. (6 分) 如图,在 $ \triangle ABD $ 中,$ \angle D = 90^{\circ},C $ 是 $ BD $ 上一点,已知 $ BC = 9,AB = 17,AC = 10 $,求 $ AD $ 的长.

答案： 设CD=x，则BD=BC+CD=9+x。在△ACD中，
∵∠D=90°，
∴AD²=AC²-CD²，在△ABD中，
∵∠D=90°，
∴AD²=AB²-BD²，
∴AC²-CD²=AB²-BD²，即10²-x²=17²-(9+x)²，解得x=6，
∴AD²=10²-6²=64，
∴AD=8。故AD的长为8。

22. (6 分) 新趋势 尺规作图 (1) 在如图①的数轴上作出表示 $ \sqrt{17} $ 的点.(不写作法,保留作图痕迹)
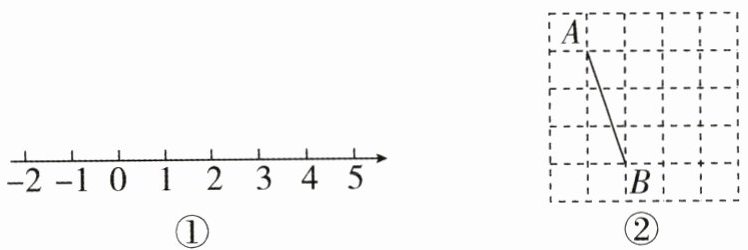
(2) 正方形网格中的每个小正方形边长都是 1,在图②中以 $ AB $ 为一边,画一个边长均为无理数的直角三角形.(说明:直角三角形的顶点均为小正方形的顶点)

答案：

23. (6 分) 新趋势 代数推理 (2024·扬州月考) 清朝的扬州籍数学家罗士琳提出了四个构造勾股数的法则,其中有两个法则如下:
①如果 $ k $ 是大于 1 的奇数,那么 $ k,\frac{k^{2} - 1}{2},\frac{k^{2} + 1}{2} $ 是一组勾股数;
②如果 $ k $ 是大于 2 的偶数,那么 $ k,(\frac{k}{2})^{2} - 1,(\frac{k}{2})^{2} + 1 $ 是一组勾股数.
请你任选其中一个法则证明它的正确性.

答案： 解（证明）：选择法则①进行证明。
已知$k$是大于$1$的奇数，要证明$k,\frac{k^{2}-1}{2},\frac{k^{2}+1}{2}$是一组勾股数，根据勾股定理，只需证明$k^{2}+(\frac{k^{2}-1}{2})^{2}=(\frac{k^{2}+1}{2})^{2}$。
左边$=k^{2}+(\frac{k^{2}-1}{2})^{2}$
$=k^{2}+\frac{k^{4}-2k^{2}+1}{4}$
$=\frac{4k^{2}+k^{4}-2k^{2}+1}{4}$
$=\frac{k^{4}+2k^{2}+1}{4}$
右边$=(\frac{k^{2}+1}{2})^{2}=\frac{k^{4}+2k^{2}+1}{4}$
左边$=$右边，所以$k,\frac{k^{2}-1}{2},\frac{k^{2}+1}{2}$是一组勾股数。
（若选择法则②证明：
已知$k$是大于$2$的偶数，要证明$k,(\frac{k}{2})^{2}-1,(\frac{k}{2})^{2}+1$是一组勾股数，根据勾股定理，只需证明$k^{2}+[(\frac{k}{2})^{2}-1]^{2}=[(\frac{k}{2})^{2}+1]^{2}$。
左边$=k^{2}+[(\frac{k}{2})^{2}-1]^{2}$
$=k^{2}+(\frac{k^{2}}{4}-1)^{2}$
$=k^{2}+\frac{k^{4}}{16}-\frac{k^{2}}{2}+1$
$=\frac{k^{4}}{16}+\frac{k^{2}}{2}+1$
右边$=[(\frac{k}{2})^{2}+1]^{2}=(\frac{k^{2}}{4}+1)^{2}=\frac{k^{4}}{16}+\frac{k^{2}}{2}+1$
左边$=$右边，所以$k,(\frac{k}{2})^{2}-1,(\frac{k}{2})^{2}+1$是一组勾股数。）