第110页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
7. (潍坊中考)记实数$x_1,x_2,…,x_n中的最小数为\min\{x_1,x_2,…,x_n\}$,例如$\min\{-1,1,2\} = -1$,则函数$y = \min\{2x - 1,x,4 - x\}$的图象大为 (
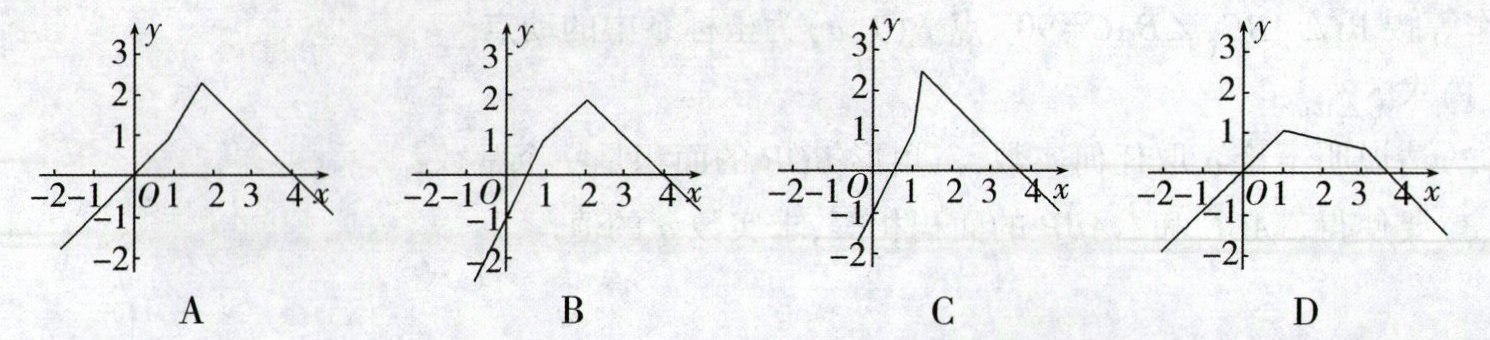
B
)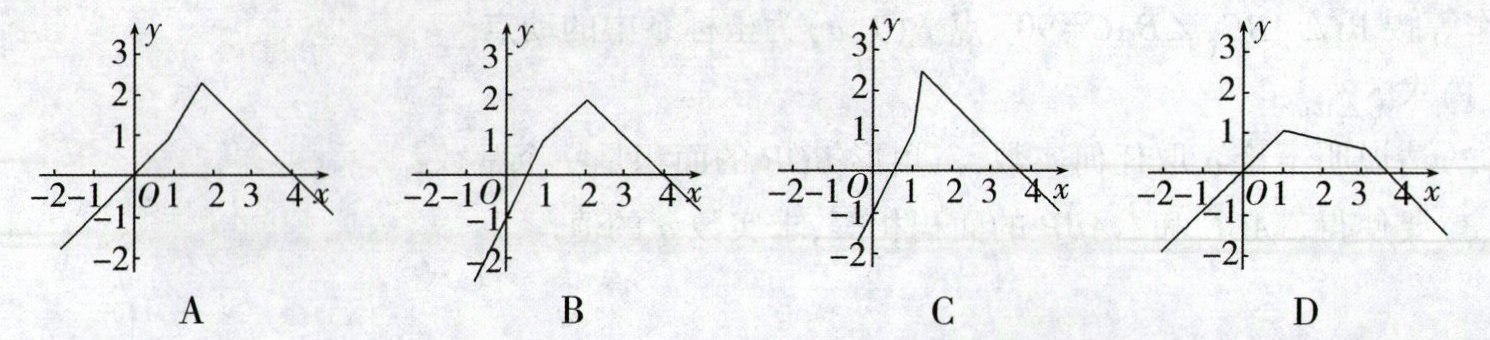
答案:
B [解析]如图所示为函数y=x,y=2x−1,y=4−x的图象,可得$y = \begin{cases}2x - 1, & x < 1\\x, & 1\leq x\leq 2\\4 - x, & x > 2\end{cases}$。故选B。
8. (2024·淄博中考)某日,甲、乙两人相约在一条笔直的健身道路上锻炼.两人都从A地匀速出发,甲健步走向B地.途中偶遇一位朋友,驻足交流10 min后,继续以原速步行前进;乙因故比甲晚出发30 min,跑步到达B地后立刻以原速返回,在返回途中与甲第二次相遇.下图表示甲、乙两人之间的距离y(m)与甲出发的时间x(min)之间的函数关系.
那么以下结论:
①甲、乙两人第一次相遇时,乙的锻炼用时为20 min;
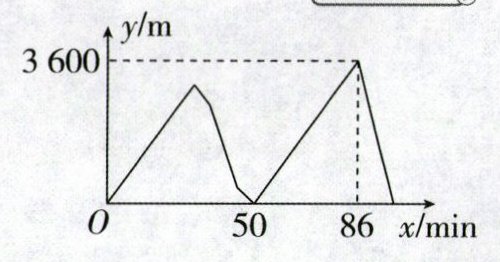
②甲出发86 min时,甲、乙两人之间的距离达到最大值3600 m;
③甲、乙两人第二次相遇的时间是在甲出发后100 min;
④A,B两地之间的距离是11200 m.
其中正确的结论有 (
A.①②③
B.①②④
C.①③④
D.②③④
那么以下结论:
①甲、乙两人第一次相遇时,乙的锻炼用时为20 min;

②甲出发86 min时,甲、乙两人之间的距离达到最大值3600 m;
③甲、乙两人第二次相遇的时间是在甲出发后100 min;
④A,B两地之间的距离是11200 m.
其中正确的结论有 (
B
)A.①②③
B.①②④
C.①③④
D.②③④
答案:
B [解析]①
∵乙比甲晚出发30min,且当x=50时,y=0,
∴乙出发50−30=20(min)时,两人第一次相遇,即甲、乙两人第一次相遇时,乙的锻炼用时为20min,结论①正确;②观察函数图象,可知,当x=86时,y取得最大值,最大值为3600,
∴甲出发86min时,甲、乙两人之间的距离达到最大值3600m,结论②正确;③设甲的速度为x m/min,乙的速度为y m/min,根据题意,得$\begin{cases}(50 - 10)x = (50 - 30)y\\(86 - 30)y - (86 - 10)x = 3600\end{cases}$,解得$\begin{cases}x = 100\\y = 200\end{cases}$,
∴$86 + \frac{3600}{x + y}=86 + \frac{3600}{100 + 200}=98$,
∴甲、乙两人第二次相遇的时间是在甲出发后98min,结论③错误;④
∵200×(86−30)=11200(m),
∴A,B两地之间的距离是11200m,结论④正确.综上所述,正确的结论有①②④.故选B.
∵乙比甲晚出发30min,且当x=50时,y=0,
∴乙出发50−30=20(min)时,两人第一次相遇,即甲、乙两人第一次相遇时,乙的锻炼用时为20min,结论①正确;②观察函数图象,可知,当x=86时,y取得最大值,最大值为3600,
∴甲出发86min时,甲、乙两人之间的距离达到最大值3600m,结论②正确;③设甲的速度为x m/min,乙的速度为y m/min,根据题意,得$\begin{cases}(50 - 10)x = (50 - 30)y\\(86 - 30)y - (86 - 10)x = 3600\end{cases}$,解得$\begin{cases}x = 100\\y = 200\end{cases}$,
∴$86 + \frac{3600}{x + y}=86 + \frac{3600}{100 + 200}=98$,
∴甲、乙两人第二次相遇的时间是在甲出发后98min,结论③错误;④
∵200×(86−30)=11200(m),
∴A,B两地之间的距离是11200m,结论④正确.综上所述,正确的结论有①②④.故选B.
9. (2024·西藏中考)将正比例函数$y = 2x$的图象向上平移3个单位长度后得到函数图象的表达式为
y=2x+3
.
答案:
y=2x+3 [解析]正比例函数y=2x的图象向上平移3个单位长度后得到函数图象的表达式为y=2x+3.
10. 新趋势开放性试题(2024·潍坊中考)请写出同时满足以下两个条件的一个函数:
y=−x+2(答案不唯一)
.
答案:
y=−x+2(答案不唯一) [解析]
∵y随着x的增大而减小,
∴一次函数的比例系数k<0.又
∵函数图象与y轴正半轴相交,
∴b>0,
∴同时满足两个条件的一次函数可以是y=−x+2 (答案不唯一).
∵y随着x的增大而减小,
∴一次函数的比例系数k<0.又
∵函数图象与y轴正半轴相交,
∴b>0,
∴同时满足两个条件的一次函数可以是y=−x+2 (答案不唯一).
11. (2024·湖北中考)铁的密度为$7.9g/cm^3$,铁块的质量m(单位:g)与它的体积V(单位:$cm^3$)之间的函数表达式为$m = 7.9V$.当$V = 10cm^3$时,$m= $
79
g.
答案:
79 [解析]当V=10时,m=7.9×10=79(g).
12. (黑龙江中考)在函数$y = \sqrt{2x - 3}$中,自变量x的取值范围是
x≥$\frac{3}{2}$
.
答案:
x≥$\frac{3}{2}$ [解析]由题意得2x−3≥0⇒x≥$\frac{3}{2}$.
13. 若正比例函数$y = -(m - 1)x$的函数值y随x的增大而减小,且函数图象上的点到两坐标轴距离相等,则m的值为
2
.
答案:
2 [解析]由题意得−(m−1)=−1,解得m=2.
14. 已知一次函数的图象经过点$(-\frac{1}{2},-\frac{1}{4})$,且图象与x轴的交点到原点的距离为1,则该函数的表达式为
y=−$\frac{1}{2}$x−$\frac{1}{2}$或y=$\frac{1}{6}$x−$\frac{1}{6}$
.
答案:
y=−$\frac{1}{2}$x−$\frac{1}{2}$或y=$\frac{1}{6}$x−$\frac{1}{6}$ [解析]当与x轴的交点为(−1,0)时解得函数的表达式为y=−$\frac{1}{2}$x−$\frac{1}{2}$,当与x轴的交点为(1,0)时解得函数的表达式为y=$\frac{1}{6}$x−$\frac{1}{6}$.
15. (2024·日照中考)已知一次函数$y_1 = ax(a\neq0)$和$y_2 = \frac{1}{2}x + 1$,当$x\leqslant1$时,函数$y_2$的图象在函数$y_1$的图象上方,则a的取值范围为
$\frac{1}{2}\leqslant a\lt\frac{3}{2}$
.
答案:
$\frac{1}{2}$≤a<$\frac{3}{2}$ [解析]如图,可知y₁=ax过原点.
∵y₂=$\frac{1}{2}$x+1中,当x=1时,y₂=$\frac{3}{2}$,
∴当y₁=ax过点(1,$\frac{3}{2}$)时,$\frac{3}{2}$=a×1,得a=$\frac{3}{2}$.当y₁=ax与y₂=$\frac{1}{2}$x+1平行时,得a=$\frac{1}{2}$.由函数图象知,当x≤1时,函数y₂的图象在函数y=$\frac{1}{2}$x的图象上方,a的取值范围为$\frac{1}{2}$≤a<$\frac{3}{2}$.
∵y₂=$\frac{1}{2}$x+1中,当x=1时,y₂=$\frac{3}{2}$,
∴当y₁=ax过点(1,$\frac{3}{2}$)时,$\frac{3}{2}$=a×1,得a=$\frac{3}{2}$.当y₁=ax与y₂=$\frac{1}{2}$x+1平行时,得a=$\frac{1}{2}$.由函数图象知,当x≤1时,函数y₂的图象在函数y=$\frac{1}{2}$x的图象上方,a的取值范围为$\frac{1}{2}$≤a<$\frac{3}{2}$.
16. (2024·南通中考)在平面直角坐标系xOy中,已知$A(3,0)$,$B(0,3)$.直线$y = kx + b$(k,b为常数,且$k\gt0$)经过点$(1,0)$,并把$\triangle AOB$分成两部分,其中靠近原点部分的面积为$\frac{15}{4}$,则k的值为
$\frac{3}{5}$
答案:
$\frac{3}{5}$ [解析]根据题意画出图象如下,设直线AB的表达式为y=mx+n,把A(3,0),B(0,3)代入,可得$\begin{cases}3m + n = 0\\n = 3\end{cases}$,解得$\begin{cases}m = -1\\n = 3\end{cases}$,
∴直线AB的表达式为y=−x+3.
∵直线y=kx+b经过点C(1,0),
∴k+b=0,
∴b=−k,
∴直线y=kx−k,联立两直线方程$\begin{cases}y = kx - k\\y = -x + 3\end{cases}$,解得$\begin{cases}x = \frac{k + 3}{k + 1}\\y = \frac{2k}{k + 1}\end{cases}$,
∴D($\frac{k + 3}{k + 1}$,$\frac{2k}{k + 1}$).
∵A(3,0),B(0,3),C(1,0),
∴OB=3,OA=3,AC=2,根据题意有S△ABO−S△ACD=$\frac{15}{4}$,即$\frac{1}{2}$·OB·OA−$\frac{1}{2}$·y_D·AC=$\frac{15}{4}$,$\frac{1}{2}$×3×3−$\frac{1}{2}$×$\frac{2k}{k + 1}$×2=$\frac{15}{4}$,解得k=$\frac{3}{5}$.
∴直线AB的表达式为y=−x+3.
∵直线y=kx+b经过点C(1,0),
∴k+b=0,
∴b=−k,
∴直线y=kx−k,联立两直线方程$\begin{cases}y = kx - k\\y = -x + 3\end{cases}$,解得$\begin{cases}x = \frac{k + 3}{k + 1}\\y = \frac{2k}{k + 1}\end{cases}$,
∴D($\frac{k + 3}{k + 1}$,$\frac{2k}{k + 1}$).
∵A(3,0),B(0,3),C(1,0),
∴OB=3,OA=3,AC=2,根据题意有S△ABO−S△ACD=$\frac{15}{4}$,即$\frac{1}{2}$·OB·OA−$\frac{1}{2}$·y_D·AC=$\frac{15}{4}$,$\frac{1}{2}$×3×3−$\frac{1}{2}$×$\frac{2k}{k + 1}$×2=$\frac{15}{4}$,解得k=$\frac{3}{5}$.
查看更多完整答案,请扫码查看


