《2025年学霸提优大试卷八年级数学上册苏科版》

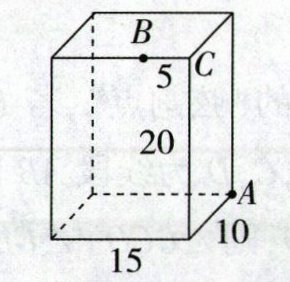
8. 如图,长方体的长为15,宽为10,高为20,点$B离点C$的距离为5,一只蚂蚁如果要沿着长方体的表面从点$A爬到点B$,需要爬行的最短距离是 ( )


A.25
B.$\sqrt{725}$
C.35
D.$\sqrt{925}$

答案：
A　[解析] 将长方体展开,连接AB,如图①,BD = 10 + 5 = 15,AD = 20,由勾股定理得AB = $\sqrt{BD^2 + AD^2}$ = $\sqrt{15^2 + 20^2}$ = $\sqrt{625}$ = 25;如图②,BC = 5,AC = 20 + 10 = 30,由勾股定理得,AB = $\sqrt{BC^2 + AC^2}$ = $\sqrt{5^2 + 30^2}$ = $\sqrt{925}$;如图③,BD = 20 + 5 = 25,AD = 10,根据勾股定理得,AB = $\sqrt{BD^2 + AD^2}$ = $\sqrt{25^2 + 10^2}$ = $\sqrt{725}$.
∵25＜$\sqrt{725}$＜$\sqrt{925}$,故选A.

9. 已知$\triangle ABC\cong\triangle DEF$,若$BC= 5,DE= 6,DF= 7$,则$\triangle ABC$的周长为18.

答案： 18　[解析]
∵△ABC≌△DEF,
∴AB = DE = 6,AC = DF = 7,
∴△ABC的周长 = AB + AC + BC = 6 + 7 + 5 = 18.

10. 如图是两人某次棋局棋盘上的一部分,若棋盘中每个小正方形的边长为1,则“车”“炮”两棋子所在格点之间的距离为$\sqrt{10}$.

答案： $\sqrt{10}$　[解析] 由题意得，“车”“炮”两棋子所在格点之间的距离为$\sqrt{1^2 + 3^2}$ = $\sqrt{10}$.

11. 若$-2x^{m-n}y^2与3x^4y^{2m+n}$是同类项,则$m-3n$的立方根是2.

答案： 2　[解析] 若−2$x^{m - n}y^2$与3$x^4y^{2m + n}$是同类项,
∴$\begin{cases}m - n = 4 \\2m + n = 2 \end{cases}$,解方程得$\begin{cases}m = 2 \\n = - 2 \end{cases}$,
∴m - 3n = 2 - 3×( - 2)=8,8的立方根是2.

12. 新趋势数学文化(2024·安徽中考)我国古代数学家张衡将圆周率取值为$\sqrt{10}$,祖冲之给出圆周率的一种分数形式的近似值为$\frac{22}{7}$.比较大小:$\sqrt{10}$＞$\frac{22}{7}$(填“＞”或“＜”).

答案： ＞　[解析] ($\sqrt{10}$)² = 10,($\frac{22}{7}$)² = $\frac{484}{49}$,
∵10＞$\frac{484}{49}$,
∴$\sqrt{10}$＞$\frac{22}{7}$.

13. 如图,已知在四边形$ABCD$中,$\angle BCD= 90^{\circ},BD平分\angle ABC,AB= 6,BC= 9,CD= 4$,则四边形$ABCD$的面积是______30.

答案： 30　[解析] 过点D作DE⊥AB,交BA的延长线于点E,
∵∠BCD = 90°,BD平分∠ABC,
∴DE = DC = 4,
∴四边形ABCD的面积 = S△BCD + S△BAD = $\frac{1}{2}$BC·CD + $\frac{1}{2}$AB·DE = $\frac{1}{2}$×9×4 + $\frac{1}{2}$×6×4 = 30.

14. 已知$a,b$为实数,且$\sqrt{1+a}-(b-1)\sqrt{1-b}= 0$,则$a^{99}-b^{100}$的值为−2.

答案： −2　[解析]
∵$\sqrt{1 + a}$−(b - 1)$\sqrt{1 - b}$ = 0,
∴$\sqrt{1 + a}$+(1 - b)$\sqrt{1 - b}$ = 0.
∵$\sqrt{1 + a}$≥0,$\sqrt{1 - b}$≥0,
∴1 + a = 0,1 - b = 0,解得a = - 1,b = 1,
∴$a^{99} - b^{100}$ = (- 1)$^{99}$ - 1$^{100}$ = - 1 - 1 = - 2.

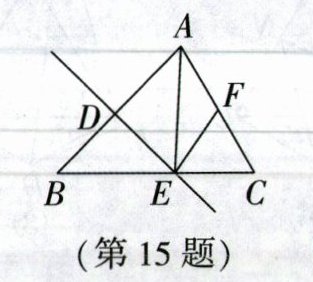
15. 如图,在$\triangle ABC$中,$\angle B= 45^{\circ},AB的垂直平分线交AB于点D$,交$BC于点E$,点$F是AC$的中点,连接$AE,EF$,若$BE= 4,AC+BC= 12$,则$\triangle CEF$的周长为______8.

答案： 8　[解析]
∵DE垂直平分AB,
∴∠BAE = ∠ABE = 45°,BE = AE = 4,
∴∠BEA = 90°,
∵AC + BC = 12,
∴AC + CE = 12 - 4 = 8,即AC = 8 - CE.在Rt△AEC中,AE² + CE² = AC²,4² + CE² = (8 - CE)²,解得CE = 3,AC = 5.又
∵点F是AC的中点,
∴EF = FC = $\frac{1}{2}$AC = $\frac{5}{2}$,
∴△CEF的周长 = CF + CE + FE = $\frac{5}{2}$ + 3 + $\frac{5}{2}$ = 8.

16. 如图,$AB// CD,\angle BCD= 90^{\circ},AB= 2,CD= 8,E为AD$的中点,连接$BE,\angle CBE= 45^{\circ}$,则$BC$的长为______.

答案：
6　[解析] 如图,延长BE交CD于点F.
∵AB//CD,
∴∠A = ∠D.
∵E为AD的中点,
∴AE = DE.在△ABE和△DFE中,$\begin{cases}\angle A = \angle D \\AE = DE \\\angle AEB = \angle DEF \end{cases}$,
∴△ABE≌△DFE(ASA),
∴AB = DF = 2.
∵CD = 8,
∴CF = CD - DF = 6.
∵∠BCD = 90°,∠CBE = 45°,
∴∠CFB = 180° - 90° - 45° = 45° = ∠CBE,
∴BC = CF = 6.

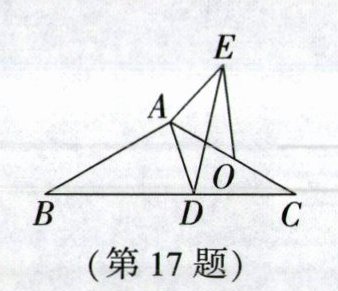
17. 如图,在$\triangle ABC$中,$AB= AC= 8,\angle C= 30^{\circ},D是BC$边上的一个动点,连接$AD$,以$AD为边作\triangle ADE$,使$AD= AE,\angle AED= \angle C.O为AC$的中点,连接$OE$,则线段$OE$的最小值为______.

答案：
2　[解析] 如图,取AB的中点G,连接DG,CG.
∵AB = AC = 8,O是AC的中点,G是AB的中点，
∴AG = BG = AO = CO = 4,
∴∠B = ∠ACB = 30°.又
∵AD = AE,
∴∠ADE = ∠AED = ∠ACB = 30°,
∴∠BAC = ∠DAE = 120°,
∴∠BAD = ∠CAE.在△ADG和△AEO中,$\begin{cases}AD = AE \\\angle GAD = \angle OAE \\AG = AO \end{cases}$,
∴△ADG≌△AEO(SAS),
∴GD = EO,
∴DG有最小值时，OE也有最小值,
∴当GD⊥BC时,GD有最小值.
∵∠B = 30°,GD⊥BC,BG = 4,
∴GD = 2,
∴线段OE的最小值为2.

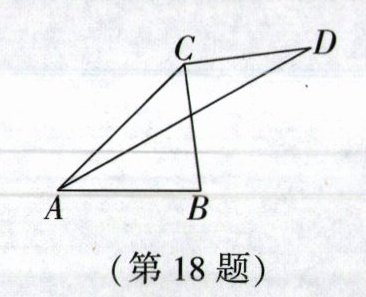
18. 如图,在$\triangle ABC$中,$\angle CAB= 45^{\circ},AC= 5,AB= 4$,过点$C作CD\perp CB$,点$D在点C$右侧,且$CD= CB$,连接$AD$,则$AD^2$的值为______.

66

答案： 66　[解析] 如图,作CE⊥AC,交AB的延长线于点E,连接DE.
∵∠CAB = 45°,
∴△ACE是等腰直角三角形,
∴CE = AC = 5,AE² = AC² + CE² = 50.
∵CD⊥CB,
∴∠BCD = ∠ACE = 90°,
∴∠BCD - ∠BCE = ∠ACE - ∠BCE,
∴∠ECD = ∠ACB.
∵CB = CD,AC = EC,
∴△ACB≌△ECD(SAS),
∴DE = AB = 4,∠CED = ∠CAB = 45°,
∴∠AED = ∠CED + ∠CEA = 90°,
∴在Rt△ADE中,AD² = AE² + DE² = 66.