第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
24. (10分)新题型新定义(2025·宿迁模拟)定义:如图①,点$M,N把线段EF分割成EM,MN和FN$,若$MN^2= EM^2+NF^2$,则称点$M,N是线段EF$的“弦割点”,其中点$M$称为“左弦点”,点$N$称“右弦点”.
(1)如图①,已知点$M,N是线段EF$的弦割点”,若$EM= 1,MN= 2$,求$FN$的长;
(2)如图②,在$Rt\triangle AOB$中,$OA= OB,C,D为线段AB$的“弦割点”,以$CD为斜边在AB上方作等腰直角三角形CDG$,连接$OC,OD$,则$\angle GCO+\angle GDO= $______;
(3)如图③,已知点$P是线段HK$的“左弦点”,请作出线段$HK$的“右弦点”$Q$.(尺规作图,保留作图痕迹)
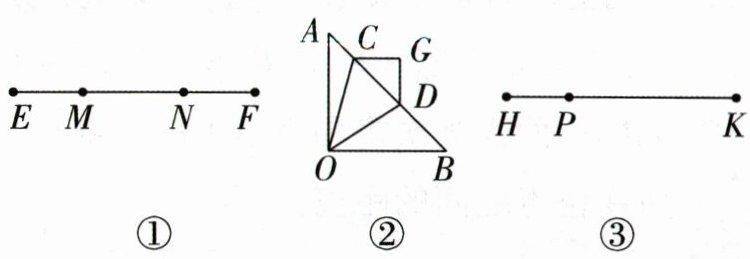
(1)如图①,已知点$M,N是线段EF$的弦割点”,若$EM= 1,MN= 2$,求$FN$的长;
(2)如图②,在$Rt\triangle AOB$中,$OA= OB,C,D为线段AB$的“弦割点”,以$CD为斜边在AB上方作等腰直角三角形CDG$,连接$OC,OD$,则$\angle GCO+\angle GDO= $______;
(3)如图③,已知点$P是线段HK$的“左弦点”,请作出线段$HK$的“右弦点”$Q$.(尺规作图,保留作图痕迹)
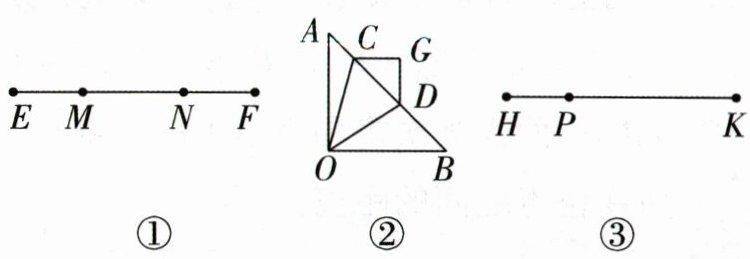
答案:
(1)
∵已知点M,N是线段EF的“弦割点”,
∴MN² = EM² + FN²,
∴2² = 1² + FN²,
∴FN = $\sqrt{3}$.
(2) 225° [解析] 如图①,
∵∠AOB = 90°,OA = OB,
∴∠OAB = ∠OBA = 45°.将△BOD绕点O逆时针旋转90°至△AOE,连接CE,
∴∠OAE = ∠OBD = 45°,AE = BD,OE = OD,∠BOD = ∠AOE,
∴∠BAE = ∠OAE + ∠OAB = 90°,
∴CE² = AE² + AC² = BD² + AC².
∵C,D为线段AB的“弦割点”,
∴CD² = BD² + AC²,
∴CD = CE;
∵OC = OC,
∴△COE≌△COD(SSS),
∴∠COE = ∠COD,
∴∠COD = ∠AOE + ∠AOC = ∠BOD + ∠AOC;
∵∠COD + ∠BOD + ∠AOC = 90°,
∴∠COD = 45°.
∵△CDG是等腰直角三角形,
∴∠G = 90°,
∴∠GCO + ∠GDO = 360° - 90° - 45° = 225°.
(3) 如图②,(Ⅰ)作HK的垂直平分线AB,交HK于点B,在AB上截取BA = BH;(Ⅱ)连接AP,作CA⊥AP;(Ⅲ)作∠PAC的平分线AQ,交HK于点Q,则Q是求作的点.

(1)
∵已知点M,N是线段EF的“弦割点”,
∴MN² = EM² + FN²,
∴2² = 1² + FN²,
∴FN = $\sqrt{3}$.
(2) 225° [解析] 如图①,
∵∠AOB = 90°,OA = OB,
∴∠OAB = ∠OBA = 45°.将△BOD绕点O逆时针旋转90°至△AOE,连接CE,
∴∠OAE = ∠OBD = 45°,AE = BD,OE = OD,∠BOD = ∠AOE,
∴∠BAE = ∠OAE + ∠OAB = 90°,
∴CE² = AE² + AC² = BD² + AC².
∵C,D为线段AB的“弦割点”,
∴CD² = BD² + AC²,
∴CD = CE;
∵OC = OC,
∴△COE≌△COD(SSS),
∴∠COE = ∠COD,
∴∠COD = ∠AOE + ∠AOC = ∠BOD + ∠AOC;
∵∠COD + ∠BOD + ∠AOC = 90°,
∴∠COD = 45°.
∵△CDG是等腰直角三角形,
∴∠G = 90°,
∴∠GCO + ∠GDO = 360° - 90° - 45° = 225°.
(3) 如图②,(Ⅰ)作HK的垂直平分线AB,交HK于点B,在AB上截取BA = BH;(Ⅱ)连接AP,作CA⊥AP;(Ⅲ)作∠PAC的平分线AQ,交HK于点Q,则Q是求作的点.


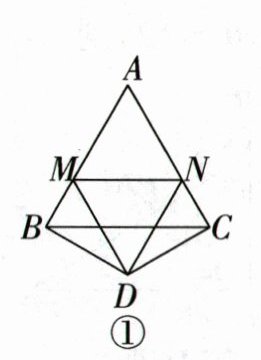
25. (10分)等边三角形$ABC的两边AB,AC所在直线上分别有点M,N,D为\triangle ABC$外一点,且$\angle MDN= 60^{\circ},\angle BDC= 120^{\circ},BD= CD$.当点$M,N分别在直线AB,AC$上移动时,探究$BM,CN,MN之间的数量关系以及\triangle AMN的周长Q与等边三角形ABC的周长L$的关系.
(1)如图①,当点$M,N分别在边AB,AC$上,且$DM= DN$时,$BM,CN,MN$之间的数量关系式为______,此时$\frac{Q}{L}$的值是______.
(2)如图②,当点$M,N分别在边AB,AC$上,且$DM\neq DN$时,猜想(1)问的两个结论还成立吗?写出你的猜想并加以证明.
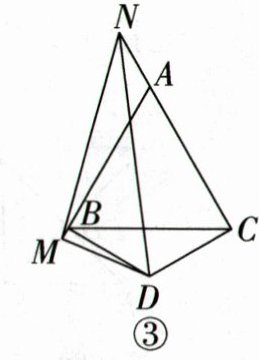
(3)如图③,当点$M,N分别在边AB,CA$的延长线上时,若$AN= x$,试用含$x,L的代数式表示Q$.
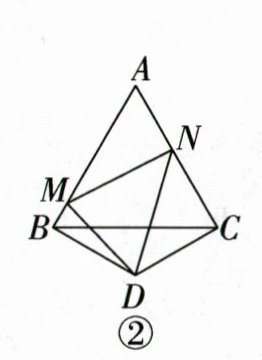
(1)如图①,当点$M,N分别在边AB,AC$上,且$DM= DN$时,$BM,CN,MN$之间的数量关系式为______,此时$\frac{Q}{L}$的值是______.
(2)如图②,当点$M,N分别在边AB,AC$上,且$DM\neq DN$时,猜想(1)问的两个结论还成立吗?写出你的猜想并加以证明.
(3)如图③,当点$M,N分别在边AB,CA$的延长线上时,若$AN= x$,试用含$x,L的代数式表示Q$.



答案:
(1) BM + CN = MN,$\frac{2}{3}$ [解析]
∵DM = DN,∠MDN = 60°,
∴△MDN是等边三角形.
∵△ABC是等边三角形,
∴∠A = 60°.
∵BD = CD,∠BDC = 120°,
∴∠DBC = ∠DCB = 30°,
∴∠MBD = ∠NCD = 90°.
∵DM = DN,BD = CD,
∴Rt△BDM≌Rt△CDN(HL),
∴∠BDM = ∠CDN = 30°,BM = CN,
∴DM = 2BM,DN = 2CN,
∴MN = 2BM = 2CN = BM + CN,
∴AM = AN,
∴△AMN是等边三角形.
∵AB = AM + BM,
∴AM:AB = 2:3,
∴$\frac{Q}{L}$ = $\frac{2}{3}$.
(2) 猜想:结论仍然成立.证明:如图①,延长AC至点$M_1$,使$CM_1$ = BM,连接$DM_1$.由
(1)知∠MBD = ∠$M_1$CD = 90°,
∵BD = CD,
∴△DBM≌△D$M_1$C(SAS),
∴DM = D$M_1$.
∵∠MDN = 60°,∠BDC = 120°,
∴∠$M_1$DN = ∠MDN = 60°,
∴△MDN≌△$M_1$DN(SAS),
∴MN = $M_1$N = $M_1$C + CN = BM + CN,
∴△AMN的周长为AM + MN + AN = AM + BM + CN + AN = AB + AC,
∴$\frac{Q}{L}$ = $\frac{2}{3}$.
(3) 如图②,在CN上截取$CM_2$ = BM,连接$DM_2$.由
(1)知∠MBD = ∠$M_2$CD = 90°,
∵BD = CD,
∴△DBM≌△D$M_2$C(SAS),
∴DM = D$M_2$.
∵∠MDN = 60°,∠BDC = 120°,
∴∠$M_2$DN = ∠MDN = 60°,
∴△MDN≌△$M_2$DN(SAS),
∴MN = $M_2$N,
∴NC - BM = MN.
∵等边三角形ABC的周长为L,
∴AB = $\frac{L}{3}$,△AMN的周长Q = MN + AN + AM = NC - BM + AN + AB + BM = AN + AC + AN + AB = 2AN + 2AB = 2x + $\frac{2}{3}$L,即Q = 2x + $\frac{2}{3}$L.

(1) BM + CN = MN,$\frac{2}{3}$ [解析]
∵DM = DN,∠MDN = 60°,
∴△MDN是等边三角形.
∵△ABC是等边三角形,
∴∠A = 60°.
∵BD = CD,∠BDC = 120°,
∴∠DBC = ∠DCB = 30°,
∴∠MBD = ∠NCD = 90°.
∵DM = DN,BD = CD,
∴Rt△BDM≌Rt△CDN(HL),
∴∠BDM = ∠CDN = 30°,BM = CN,
∴DM = 2BM,DN = 2CN,
∴MN = 2BM = 2CN = BM + CN,
∴AM = AN,
∴△AMN是等边三角形.
∵AB = AM + BM,
∴AM:AB = 2:3,
∴$\frac{Q}{L}$ = $\frac{2}{3}$.
(2) 猜想:结论仍然成立.证明:如图①,延长AC至点$M_1$,使$CM_1$ = BM,连接$DM_1$.由
(1)知∠MBD = ∠$M_1$CD = 90°,
∵BD = CD,
∴△DBM≌△D$M_1$C(SAS),
∴DM = D$M_1$.
∵∠MDN = 60°,∠BDC = 120°,
∴∠$M_1$DN = ∠MDN = 60°,
∴△MDN≌△$M_1$DN(SAS),
∴MN = $M_1$N = $M_1$C + CN = BM + CN,
∴△AMN的周长为AM + MN + AN = AM + BM + CN + AN = AB + AC,
∴$\frac{Q}{L}$ = $\frac{2}{3}$.
(3) 如图②,在CN上截取$CM_2$ = BM,连接$DM_2$.由
(1)知∠MBD = ∠$M_2$CD = 90°,
∵BD = CD,
∴△DBM≌△D$M_2$C(SAS),
∴DM = D$M_2$.
∵∠MDN = 60°,∠BDC = 120°,
∴∠$M_2$DN = ∠MDN = 60°,
∴△MDN≌△$M_2$DN(SAS),
∴MN = $M_2$N,
∴NC - BM = MN.
∵等边三角形ABC的周长为L,
∴AB = $\frac{L}{3}$,△AMN的周长Q = MN + AN + AM = NC - BM + AN + AB + BM = AN + AC + AN + AB = 2AN + 2AB = 2x + $\frac{2}{3}$L,即Q = 2x + $\frac{2}{3}$L.


查看更多完整答案,请扫码查看


