第76页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
21. (6 分)(2025·西安模拟)冬至是我国重要的传统节气之一,民间流传着谚语“冬至不端饺子碗,冻掉耳朵没人管”.某饭店准备了虾仁、羊肉两种饺子共 200 斤进行销售,其中虾仁饺子的数量不高于羊肉饺子数量的一半.已知虾仁饺子的利润为 9 元/斤,羊肉饺子的利润为 5 元/斤.设准备了虾仁饺子 $ m $($ m $ 为正整数)斤,这 200 斤饺子的销售总利润为 $ w $ 元(假设这 200 斤饺子均可售出).
(1)求 $ w $ 与 $ m $ 之间的函数表达式.
(2)该饭店如何准备这两种饺子的数量,才能获利最大?
(1)求 $ w $ 与 $ m $ 之间的函数表达式.
(2)该饭店如何准备这两种饺子的数量,才能获利最大?
答案:
(1)由题意知,准备了虾仁饺子m(m为正整数)斤,
∴准备了羊肉饺子(200-m)斤,
∴销售总利润为w=9m+5(200-m)=4m+1000.
(2)已知虾仁饺子的数量不高于羊肉饺子数量的一半,
∴m≤1/2(200-m),解得m≤66 2/3.
∵w=4m+1000,
∴w随m的增大而增大.
∵m为正整数,
∴当m=66时,w有最大值,w_最大=4×66+1000=1264.
∴200-66=134(斤).答:该饭店准备虾仁饺子66斤,羊肉饺子134斤时,才能使获利最大.
(1)由题意知,准备了虾仁饺子m(m为正整数)斤,
∴准备了羊肉饺子(200-m)斤,
∴销售总利润为w=9m+5(200-m)=4m+1000.
(2)已知虾仁饺子的数量不高于羊肉饺子数量的一半,
∴m≤1/2(200-m),解得m≤66 2/3.
∵w=4m+1000,
∴w随m的增大而增大.
∵m为正整数,
∴当m=66时,w有最大值,w_最大=4×66+1000=1264.
∴200-66=134(斤).答:该饭店准备虾仁饺子66斤,羊肉饺子134斤时,才能使获利最大.
22. (8 分)如图,在平面直角坐标系中,点 $ A(2,m) $ 在直线 $ y = 2x - 3 $ 上,过点 $ A $ 的直线交 $ y $ 轴于点 $ B(0,3) $.
(1)求 $ m $ 的值和直线 $ AB $ 的函数表达式;
(2)若点 $ P(t,y_1) $ 在直线 $ AB $ 上,点 $ Q(t + 1,y_2) $ 在直线 $ y = 2x - 3 $ 上,判断 $ 2y_1 + y_2 $ 的值是否随 $ t $ 的变化而变化,若不变,求出这个值;若变化,求出它的取值范围.
]

(1)求 $ m $ 的值和直线 $ AB $ 的函数表达式;
(2)若点 $ P(t,y_1) $ 在直线 $ AB $ 上,点 $ Q(t + 1,y_2) $ 在直线 $ y = 2x - 3 $ 上,判断 $ 2y_1 + y_2 $ 的值是否随 $ t $ 的变化而变化,若不变,求出这个值;若变化,求出它的取值范围.
]

答案:
1. (1)
求$m$的值:
因为点$A(2,m)$在直线$y = 2x−3$上,将$x = 2$代入$y = 2x−3$中,根据函数值的计算方法$y=2×2 - 3$。
计算可得$y=4 - 3=1$,所以$m = 1$,则$A(2,1)$。
求直线$AB$的函数表达式:
设直线$AB$的函数表达式为$y=kx + b(k\neq0)$。
把$A(2,1)$,$B(0,3)$代入$y = kx + b$中,得到方程组$\begin{cases}2k + b=1\\b = 3\end{cases}$。
将$b = 3$代入$2k + b=1$,得$2k+3 = 1$。
移项可得$2k=1 - 3=-2$,解得$k=-1$。
所以直线$AB$的函数表达式为$y=-x + 3$。
2. (2)
因为点$P(t,y_1)$在直线$AB:y=-x + 3$上,所以$y_1=-t + 3$。
因为点$Q(t + 1,y_2)$在直线$y = 2x−3$上,所以$y_2=2(t + 1)-3$。
展开$y_2=2(t + 1)-3$得$y_2=2t+2 - 3=2t - 1$。
计算$2y_1 + y_2$的值:
把$y_1=-t + 3$,$y_2=2t - 1$代入$2y_1 + y_2$,得$2(-t + 3)+(2t - 1)$。
根据乘法分配律$a(b + c)=ab+ac$,$2(-t + 3)+(2t - 1)=-2t+6 + 2t - 1$。
合并同类项$(-2t+2t)+(6 - 1)=5$。
综上,(1)$m = 1$,直线$AB$的函数表达式为$y=-x + 3$;(2)$2y_1 + y_2$的值不随$t$的变化而变化,值为$5$。
求$m$的值:
因为点$A(2,m)$在直线$y = 2x−3$上,将$x = 2$代入$y = 2x−3$中,根据函数值的计算方法$y=2×2 - 3$。
计算可得$y=4 - 3=1$,所以$m = 1$,则$A(2,1)$。
求直线$AB$的函数表达式:
设直线$AB$的函数表达式为$y=kx + b(k\neq0)$。
把$A(2,1)$,$B(0,3)$代入$y = kx + b$中,得到方程组$\begin{cases}2k + b=1\\b = 3\end{cases}$。
将$b = 3$代入$2k + b=1$,得$2k+3 = 1$。
移项可得$2k=1 - 3=-2$,解得$k=-1$。
所以直线$AB$的函数表达式为$y=-x + 3$。
2. (2)
因为点$P(t,y_1)$在直线$AB:y=-x + 3$上,所以$y_1=-t + 3$。
因为点$Q(t + 1,y_2)$在直线$y = 2x−3$上,所以$y_2=2(t + 1)-3$。
展开$y_2=2(t + 1)-3$得$y_2=2t+2 - 3=2t - 1$。
计算$2y_1 + y_2$的值:
把$y_1=-t + 3$,$y_2=2t - 1$代入$2y_1 + y_2$,得$2(-t + 3)+(2t - 1)$。
根据乘法分配律$a(b + c)=ab+ac$,$2(-t + 3)+(2t - 1)=-2t+6 + 2t - 1$。
合并同类项$(-2t+2t)+(6 - 1)=5$。
综上,(1)$m = 1$,直线$AB$的函数表达式为$y=-x + 3$;(2)$2y_1 + y_2$的值不随$t$的变化而变化,值为$5$。
23. (8 分)(2023·淮安中考)快车和慢车同时从甲地出发,以各自的速度匀速向乙地行驶,快车到达乙地卸装货物用时 30 min,结束后,立即按原路以另一速度匀速返回,直至与慢车相遇,已知慢车的速度为 $ 70 km/h $.两车之间的距离 $ y(km) $ 与慢车行驶的时间 $ x(h) $ 的函数图象如图所示.
(1)请解释图中点 $ A $ 的实际意义;
(2)求图中线段 $ AB $ 所表示的函数表达式;
(3)两车相遇后,如果快车以返回的速度继续向甲地行驶,求到达甲地还需多长时间.
]
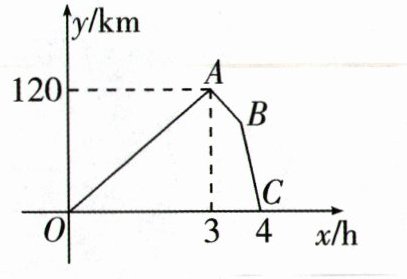
(1)请解释图中点 $ A $ 的实际意义;
(2)求图中线段 $ AB $ 所表示的函数表达式;
(3)两车相遇后,如果快车以返回的速度继续向甲地行驶,求到达甲地还需多长时间.
]

答案:
1. (1)
点$A$的实际意义:快车在慢车行驶$3h$时到达乙地。
2. (2)
解:
慢车速度$v_{慢}=70km/h$,设快车去时速度为$v_{快}$。
根据$3h$时两车距离$120km$,由$y=(v_{快}-v_{慢})x$,可得$120=(v_{快}-70)×3$。
解方程$120 = 3v_{快}-210$,$3v_{快}=120 + 210$,$v_{快}=110km/h$。
甲地到乙地的距离$s = 110×3=330km$。
$B$点横坐标$x = 3+\frac{30}{60}=3.5$,纵坐标$y = 120-70×0.5=120 - 35 = 85$,即$B(3.5,85)$,$A(3,120)$。
设线段$AB$的函数表达式为$y=kx + b$,把$A(3,120)$,$B(3.5,85)$代入得$\begin{cases}3k + b=120\\3.5k + b=85\end{cases}$。
用第一个方程减第二个方程:$(3k + b)-(3.5k + b)=120 - 85$,$3k + b-3.5k - b = 35$,$-0.5k=35$,解得$k=-70$。
把$k = - 70$代入$3k + b=120$,$3×(-70)+b=120$,$b=120 + 210=330$。
所以线段$AB$的函数表达式为$y=-70x + 330(3\leqslant x\leqslant3.5)$。
3. (3)
解:
$C$点横坐标$x = 4$,此时慢车行驶路程$s_{慢}=70×4 = 280km$,快车返回时与慢车的速度和$v=85÷(4 - 3.5)=170km/h$,则快车返回速度$v_{快返}=170 - 70=100km/h$。
两车相遇时,快车离甲地距离$s'=330-(170×(4 - 3.5))=330 - 85 = 245km$。
时间$t=\frac{245}{100}=2.45h$。
综上,(1)快车在慢车行驶$3h$时到达乙地;(2)$y=-70x + 330(3\leqslant x\leqslant3.5)$;(3)$2.45h$。
点$A$的实际意义:快车在慢车行驶$3h$时到达乙地。
2. (2)
解:
慢车速度$v_{慢}=70km/h$,设快车去时速度为$v_{快}$。
根据$3h$时两车距离$120km$,由$y=(v_{快}-v_{慢})x$,可得$120=(v_{快}-70)×3$。
解方程$120 = 3v_{快}-210$,$3v_{快}=120 + 210$,$v_{快}=110km/h$。
甲地到乙地的距离$s = 110×3=330km$。
$B$点横坐标$x = 3+\frac{30}{60}=3.5$,纵坐标$y = 120-70×0.5=120 - 35 = 85$,即$B(3.5,85)$,$A(3,120)$。
设线段$AB$的函数表达式为$y=kx + b$,把$A(3,120)$,$B(3.5,85)$代入得$\begin{cases}3k + b=120\\3.5k + b=85\end{cases}$。
用第一个方程减第二个方程:$(3k + b)-(3.5k + b)=120 - 85$,$3k + b-3.5k - b = 35$,$-0.5k=35$,解得$k=-70$。
把$k = - 70$代入$3k + b=120$,$3×(-70)+b=120$,$b=120 + 210=330$。
所以线段$AB$的函数表达式为$y=-70x + 330(3\leqslant x\leqslant3.5)$。
3. (3)
解:
$C$点横坐标$x = 4$,此时慢车行驶路程$s_{慢}=70×4 = 280km$,快车返回时与慢车的速度和$v=85÷(4 - 3.5)=170km/h$,则快车返回速度$v_{快返}=170 - 70=100km/h$。
两车相遇时,快车离甲地距离$s'=330-(170×(4 - 3.5))=330 - 85 = 245km$。
时间$t=\frac{245}{100}=2.45h$。
综上,(1)快车在慢车行驶$3h$时到达乙地;(2)$y=-70x + 330(3\leqslant x\leqslant3.5)$;(3)$2.45h$。
查看更多完整答案,请扫码查看


