《2025年学霸提优大试卷八年级数学上册苏科版》

1. (2024·石家庄模拟)如图,数轴上点 $ A,B,C,D $ 对应的数分别是 $-1,1,x,7$, 点 $ C $ 在线段 $ BD $ 上且不与端点重合,若线段 $ AB,BC,CD $ 能围成三角形,则 $ x $ 可能是 (C)

A.2
B.3
C.4
D.5

答案： C　　[解析]由点在数轴上的位置,得AB=1−(−1)=2,BC=x−1,CD=7−x.由三角形三边关系,得{(x - 1)+7 - x＞2 ①,2+x - 1＞7 - x ②,2+7 - x＞x - 1 ③,不等式①恒成立;由不等式②,得x＞3;由不等式③,得x＜5,
∴不等式组的解集是3＜x＜5.故选C.

2. (2024·南通校级月考)下列条件,不能判定两个直角三角形全等的是 (B)
A.斜边和一直角边对应相等
B.两个锐角对应相等
C.一锐角和斜边对应相等
D.两条直角边对应相等

答案： B　　[解析]A.符合判定HL;B.全等三角形的判定必须有边的参与，故本选项错误;C.符合判定AAS;D.符合判定SAS.故选B.

3. 用直尺和圆规作一个角的平分线,其正确的依据是 (B)
A.AAS
B.SSS
C.SAS
D.ASA

答案： B　　[解析]以∠AOB为例,①以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;②分别以C,D为圆心,大于$\frac{1}{2}$CD长为半径作弧,两弧交于点E,连接EC,ED.射线OE即为所求.
　　理由:在△EOC和△EOD中,{OC = OD,OE = OE,CE = DE,
∴△EOC≌△EOD(SSS).故选B.

4. 新情境(2024·贵阳模拟)中国古建筑是结构决定外观,这种传统结构形式侧面很容易呈现出等腰三角形.如图所示的这种建筑剖面图,建筑屋顶是一个等腰三角形,它的底角为 $ 30^{\circ} $, 腰为 $ 10 \mathrm{~m} $,则底边上的高是 ( )

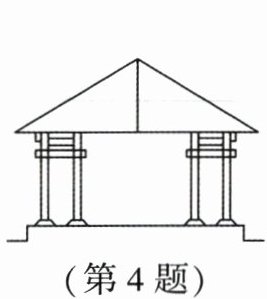
A.$ 5 \mathrm{~m} $
B.$ 10 \mathrm{~m} $
C.$ 6 \mathrm{~m} $
D.$ 8 \mathrm{~m} $

答案：
A　　[解析]如图,AD⊥BC,∠C = ∠B = 30°,AB = AC = 10m,
∴AD = $\frac{1}{2}$AB = 5m,
　　　　　　　　　　　　　　　　　　 即底边上的高是5m.故选A.

5. 如图, $ AC $ 与 $ BD $ 相交于点 $ O $, 有以下四个条件: ① $ OD= OC $; ② $ \angle C= \angle D $; ③ $ AD= BC $; ④ $ OA= OB $.从这四个条件中任选两个,不能使 $ \triangle DAO \cong \triangle CBO $ 的选法是 (C)
A.①②
B.②③
C.①③
D.①④

答案： C　　[解析]由题意知∠DOA = ∠COB,
　　选①②,可用ASA判定△DAO≌△CBO,故选项A不符合题意;选②③,可用AAS判定△DAO≌△CBO,故选项B不符合题意;选①③,不可以判定△DAO≌△CBO,故选项C符合题意;选①④,可用SAS判定△DAO≌△CBO,故选项D不符合题意.故选C.

6. 如图,已知 $ \mathrm{Rt} \triangle ABC $ 中, $ \angle C= 90^{\circ}, \angle A= 30^{\circ} $, 在直线 $ BC $ 或 $ AC $ 上取一点 $ P $, 使得 $ \triangle PAB $ 是等腰三角形,则符合条件的 $ P $ 点有 ( )

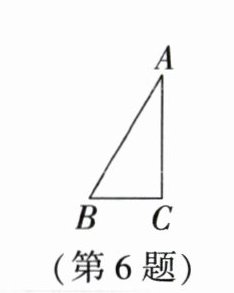
A.5 个
B.6 个
C.7 个
D.8 个

答案：
B　　[解析]如图,①作AB的垂直平分线交直线AC于点P₁,交直线BC于点P₂(此时PA = PB);②以A为圆心,AB长为半径画圆,交直线AC于点P₃,P₄,交直线BC于点P₂(此时AB = AP);③以B为圆心,BA长为半径画圆,交直线BC于点P₅,P₂,交直线AC于点P₆(此时BP = BA),符合条件的点有6个.故选B.
　　　　　　　

7. 如图,已知 $ \angle MON= 30^{\circ} $, 点 $ A_1,A_2,A_3 … $ 在射线 $ ON $ 上, 点 $ B_1,B_2,B_3 … $ 在射线 $ OM $ 上, $ \triangle A_1 B_1 A_2 $, $ \triangle A_2 B_2 A_3, \triangle A_3 B_3 A_4 … $ 均为等边三角形, 若 $ OA_1= 4 $, 则 $ \triangle A_6 B_6 A_7 $ 的边长为 ( )

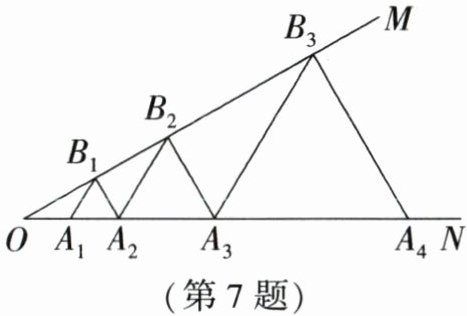
A.16
B.32
C.64
D.128

答案：
D　　[解析]如图,
∵△A₁B₁A₂是等边三角形,
∴A₁B₁ = A₂B₁ = A₁A₂,∠3 = ∠4 = ∠12 = 60°,
∴∠2 = 120°.
∵∠MON = 30°,
∴∠1 = 180° - 120° - 30° = 30°.又
∵∠3 = 60°,
∴∠5 = 180° - 60° - 30° = 90°.
∵∠MON = ∠1 = 30°,
∴OA₁ = A₁B₁ = 4,
∴A₂B₁ = 4.
∵△A₂B₂A₃,△A₃B₃A₄均为等边三角形,
∴∠11 = ∠10 = 60°,∠13 = 60°.
∵∠4 = ∠12 = 60°,
∴A₁B₁//A₂B₂//A₃B₃,B₁A₂//B₂A₃,
∴∠1 = ∠6 = ∠7 = 30°,∠5 = ∠8 = 90°,
∴A₂B₂ = 2B₁A₂,B₂A₃ = 2B₂A₃,
∴A₃B₃ = 4B₁A₂ = 16,A₄B₄ = 8B₁A₂ = 32,A₅B₅ = 16B₁A₂ = 64,以此类推:A₆B₆ = 32B₁A₂ = 128.故选D.