第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
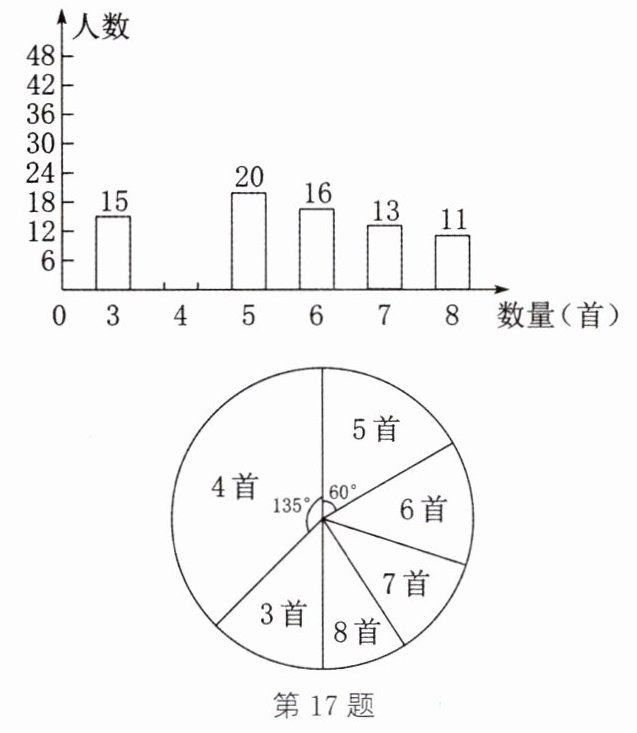
17.(14分)某校倡导全校1200名学生进行经典诗词背诵活动,并在活动之后举办经典诗词大赛。为了了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查一周的诗词背诵数量,根据调查结果绘制成的统计图(部分)如图所示。大赛结束后一个月,再次抽查这部分学生一周的诗词背诵数量,绘制成如下统计表:
|数量(首)|3|4|5|6|7|8|
|人数|10|10|15|40|25|20|
请根据调查的信息,解答下列问题:
(1)活动启动之初学生一周的诗词背诵数量的中位数为______
(2)估计大赛结束后一个月该校学生一周诗词背诵量为6首及以上的人数;
(3)选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校经典诗词背诵系列活动的效果。
|数量(首)|3|4|5|6|7|8|
|人数|10|10|15|40|25|20|
请根据调查的信息,解答下列问题:
(1)活动启动之初学生一周的诗词背诵数量的中位数为______
4.5首
;(2)估计大赛结束后一个月该校学生一周诗词背诵量为6首及以上的人数;
解:$1200×\frac{40+25+20}{10+10+15+40+25+20}=850$
(3)选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校经典诗词背诵系列活动的效果。
活动启动之初:中位数4.5首,众数4首;大赛结束后一个月:中位数6首,众数6首。从两个统计量看,活动后学生背诵量提高,效果理想。

答案:
(1) 4.5首
(2) 解:$1200×\frac{40+25+20}{10+10+15+40+25+20}=850$
(3) 活动启动之初:中位数4.5首,众数4首;大赛结束后一个月:中位数6首,众数6首。从两个统计量看,活动后学生背诵量提高,效果理想。
(1) 4.5首
(2) 解:$1200×\frac{40+25+20}{10+10+15+40+25+20}=850$
(3) 活动启动之初:中位数4.5首,众数4首;大赛结束后一个月:中位数6首,众数6首。从两个统计量看,活动后学生背诵量提高,效果理想。
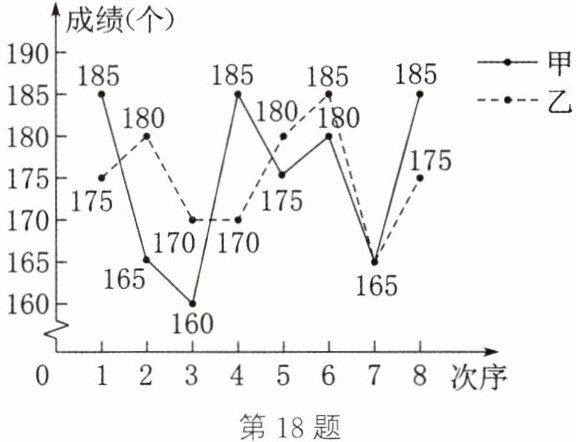
18.(14分)(恩施中考)九年级一班准备从甲、乙两名男生中选派一名参加学校组织的一分钟跳绳比赛,在相同的条件下,分别对两名男生进行了8次一分钟跳绳测试。现将测试结果绘制成如下不完整的统计表和如图所示的统计图。请根据统计图表中的信息,解答下列问题:
| |平均数(个)|中位数(个)|众数(个)|方差(个$^2)$|
|甲|175|a|b|93.75|
|乙|175|175|180,175,170|c|
(1)求a,b,c的值。
(2)若从九年级一班中选一名成绩稳定的男生参赛,你认为应选谁?请说明理由。
(3)根据以上分析,请你运用所学的统计知识,任选两个角度评价甲、乙两名男生谁的一分钟跳绳成绩更好。
| |平均数(个)|中位数(个)|众数(个)|方差(个$^2)$|
|甲|175|a|b|93.75|
|乙|175|175|180,175,170|c|
(1)求a,b,c的值。
(2)若从九年级一班中选一名成绩稳定的男生参赛,你认为应选谁?请说明理由。
(3)根据以上分析,请你运用所学的统计知识,任选两个角度评价甲、乙两名男生谁的一分钟跳绳成绩更好。

答案:
(1) 甲的成绩按从小到大排列为160,165,165,175,180,185,185,185,
中位数$a=\frac{175 + 180}{2}=177.5$,
众数$b=185$。
乙的成绩为175,180,170,170,175,180,165,185,
方差$c=\frac{1}{8}×[2×(175 - 175)^2 + 2×(180 - 175)^2 + 2×(170 - 175)^2 + (185 - 175)^2 + (165 - 175)^2]=37.5$。
(2) 应选乙。
理由:甲、乙平均数相等,乙的方差$37.5 < 93.75$,乙成绩更稳定。
(3) ①从众数看,甲的众数185高于乙的众数175,甲成绩更好;
②从中位数看,甲的中位数177.5高于乙的中位数175,甲成绩更好。
(1) 甲的成绩按从小到大排列为160,165,165,175,180,185,185,185,
中位数$a=\frac{175 + 180}{2}=177.5$,
众数$b=185$。
乙的成绩为175,180,170,170,175,180,165,185,
方差$c=\frac{1}{8}×[2×(175 - 175)^2 + 2×(180 - 175)^2 + 2×(170 - 175)^2 + (185 - 175)^2 + (165 - 175)^2]=37.5$。
(2) 应选乙。
理由:甲、乙平均数相等,乙的方差$37.5 < 93.75$,乙成绩更稳定。
(3) ①从众数看,甲的众数185高于乙的众数175,甲成绩更好;
②从中位数看,甲的中位数177.5高于乙的中位数175,甲成绩更好。
查看更多完整答案,请扫码查看


