第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
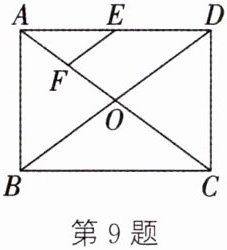
9. (吉林中考)如图,在矩形ABCD中,对角线AC,BD相交于点O,E是边AD的中点,点F在对角线AC上,且AF= $\frac{1}{4}AC$,连结EF.若AC= 10,则EF= ______.

2.5
答案:
解:
∵四边形ABCD是矩形,AC=10,
∴OA=OC=OB=OD=5(矩形对角线相等且互相平分),
∵AF=$\frac{1}{4}$AC,AC=10,
∴AF=$\frac{1}{4}$×10=2.5,
∴FC=AC-AF=10-2.5=7.5,
∵E是AD中点,
取CD中点G,连接OG,EG,
则OG是△ACD的中位线,OG=$\frac{1}{2}$AD,OG//AD,
EG是△ACD的中位线,EG=$\frac{1}{2}$AC=5,EG//AC,
∴四边形AFEG是平行四边形(两组对边分别平行),
∴EF=AG,
又
∵AG是Rt△ACD斜边上的中线(G是CD中点),
AG=$\frac{1}{2}$CD,
但矩形中AD与CD关系未直接给出,换用坐标法:
以A为原点,AB为x轴,AD为y轴,设A(0,0),C(10cosθ,10sinθ),
则O(5cosθ,5sinθ),E(0,5sinθ)(E是AD中点,AD=10sinθ),
F=AF=$\frac{1}{4}$AC,
∴F($\frac{10}{4}$cosθ,$\frac{10}{4}$sinθ)=($\frac{5}{2}$cosθ,$\frac{5}{2}$sinθ),
EF距离:$\sqrt{(0-\frac{5}{2}cosθ)^2+(5sinθ-\frac{5}{2}sinθ)^2}$=$\sqrt{(\frac{25}{4}cos^2θ)+(\frac{25}{4}sin^2θ)}$=$\sqrt{\frac{25}{4}(cos^2θ+sin^2θ)}$=$\frac{5}{2}$=2.5.
∴EF=2.5.
2.5
∵四边形ABCD是矩形,AC=10,
∴OA=OC=OB=OD=5(矩形对角线相等且互相平分),
∵AF=$\frac{1}{4}$AC,AC=10,
∴AF=$\frac{1}{4}$×10=2.5,
∴FC=AC-AF=10-2.5=7.5,
∵E是AD中点,
取CD中点G,连接OG,EG,
则OG是△ACD的中位线,OG=$\frac{1}{2}$AD,OG//AD,
EG是△ACD的中位线,EG=$\frac{1}{2}$AC=5,EG//AC,
∴四边形AFEG是平行四边形(两组对边分别平行),
∴EF=AG,
又
∵AG是Rt△ACD斜边上的中线(G是CD中点),
AG=$\frac{1}{2}$CD,
但矩形中AD与CD关系未直接给出,换用坐标法:
以A为原点,AB为x轴,AD为y轴,设A(0,0),C(10cosθ,10sinθ),
则O(5cosθ,5sinθ),E(0,5sinθ)(E是AD中点,AD=10sinθ),
F=AF=$\frac{1}{4}$AC,
∴F($\frac{10}{4}$cosθ,$\frac{10}{4}$sinθ)=($\frac{5}{2}$cosθ,$\frac{5}{2}$sinθ),
EF距离:$\sqrt{(0-\frac{5}{2}cosθ)^2+(5sinθ-\frac{5}{2}sinθ)^2}$=$\sqrt{(\frac{25}{4}cos^2θ)+(\frac{25}{4}sin^2θ)}$=$\sqrt{\frac{25}{4}(cos^2θ+sin^2θ)}$=$\frac{5}{2}$=2.5.
∴EF=2.5.
2.5
10. 如图,在Rt△ABC中,∠BAC= 90°,AB= 3,AC= 4,D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连结MN,则线段MN长的最小值为
$\frac{12}{5}$
.
答案:
解:在Rt△ABC中,∠BAC=90°,AB=3,AC=4,
由勾股定理得:BC=$\sqrt{AB^2 + AC^2} = \sqrt{3^2 + 4^2} = 5$。
∵DM⊥AB,DN⊥AC,∠BAC=90°,
∴四边形AMDN是矩形,
∴MN=AD。
当AD⊥BC时,AD的值最小。
此时,$S_{\triangle ABC} = \frac{1}{2}AB \cdot AC = \frac{1}{2}BC \cdot AD$,
即$\frac{1}{2} × 3 × 4 = \frac{1}{2} × 5 × AD$,
解得$AD = \frac{12}{5}$。
∴MN长的最小值为$\frac{12}{5}$。
$\frac{12}{5}$
由勾股定理得:BC=$\sqrt{AB^2 + AC^2} = \sqrt{3^2 + 4^2} = 5$。
∵DM⊥AB,DN⊥AC,∠BAC=90°,
∴四边形AMDN是矩形,
∴MN=AD。
当AD⊥BC时,AD的值最小。
此时,$S_{\triangle ABC} = \frac{1}{2}AB \cdot AC = \frac{1}{2}BC \cdot AD$,
即$\frac{1}{2} × 3 × 4 = \frac{1}{2} × 5 × AD$,
解得$AD = \frac{12}{5}$。
∴MN长的最小值为$\frac{12}{5}$。
$\frac{12}{5}$
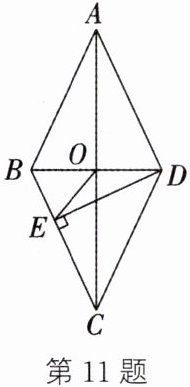
11. 如图,在菱形ABCD中,对角线AC与BD相交于点O,DE⊥BC于点E,连结OE.若∠ABC= 130°,则∠OED= ______.

25°
答案:
解:
∵四边形ABCD是菱形,
∴O为BD中点,∠DBC=∠ABC/2=130°/2=65°。
∵DE⊥BC,
∴△BDE是直角三角形,OE=BD/2=OB。
∴∠OEB=∠OBE=65°。
∵∠DEB=90°,
∴∠OED=∠DEB - ∠OEB=90° - 65°=25°。
25°
∵四边形ABCD是菱形,
∴O为BD中点,∠DBC=∠ABC/2=130°/2=65°。
∵DE⊥BC,
∴△BDE是直角三角形,OE=BD/2=OB。
∴∠OEB=∠OBE=65°。
∵∠DEB=90°,
∴∠OED=∠DEB - ∠OEB=90° - 65°=25°。
25°
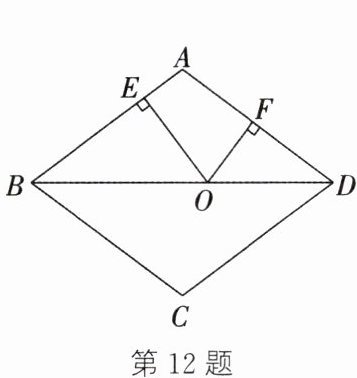
12. (南通中考)如图,在边长为10的菱形ABCD中,对角线BD= 16,O是线段BD上的动点,OE⊥AB于点E,OF⊥AD于点F,则OE+OF= ______.

答案:
$ 9.6 $ 解析:如图,连结 $ AC $,交 $ BD $ 于点 $ G $,连结 $ AO $。
∵ 四边形 $ ABCD $ 是菱形,$ BD = 16 $,
∴ $ AC \perp BD $,$ AB = AD = 10 $,$ BG = \frac{1}{2}BD = 8 $。根据勾股定理,得 $ AG = \sqrt{AB^{2} - BG^{2}} = \sqrt{10^{2} - 8^{2}} = 6 $。
∵ $ S_{\triangle ABD} = S_{\triangle AOB} + S_{\triangle AOD} $,即 $ \frac{1}{2}BD \cdot AG = \frac{1}{2}AB \cdot OE + \frac{1}{2}AD \cdot OF $,
∴ $ \frac{1}{2} × 16 × 6 = \frac{1}{2} × 10OE + \frac{1}{2} × 10OF $。
∴ $ OE + OF = 9.6 $。
$ 9.6 $ 解析:如图,连结 $ AC $,交 $ BD $ 于点 $ G $,连结 $ AO $。
∵ 四边形 $ ABCD $ 是菱形,$ BD = 16 $,
∴ $ AC \perp BD $,$ AB = AD = 10 $,$ BG = \frac{1}{2}BD = 8 $。根据勾股定理,得 $ AG = \sqrt{AB^{2} - BG^{2}} = \sqrt{10^{2} - 8^{2}} = 6 $。
∵ $ S_{\triangle ABD} = S_{\triangle AOB} + S_{\triangle AOD} $,即 $ \frac{1}{2}BD \cdot AG = \frac{1}{2}AB \cdot OE + \frac{1}{2}AD \cdot OF $,
∴ $ \frac{1}{2} × 16 × 6 = \frac{1}{2} × 10OE + \frac{1}{2} × 10OF $。
∴ $ OE + OF = 9.6 $。

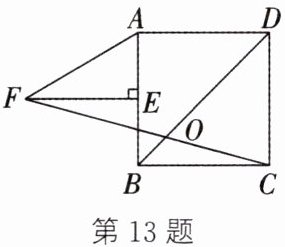
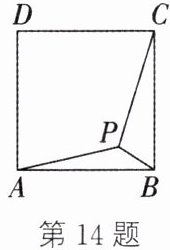
13. 如图,在正方形ABCD中,E为AB的中点,FE⊥AB,AF= 2AE,FC交BD于点O,则∠DOC的度数为______.

答案:
解:连结BF。
∵E为AB中点,
∴AB=2AE。
∵AF=2AE,
∴AB=AF。
∵FE⊥AB,E为AB中点,
∴AF=BF。
∴AF=AB=BF,△ABF为等边三角形,∠AFB=60°。
∵AF=FB,EF⊥AB,
∴∠AFE=∠EFB=30°。
∵四边形ABCD为正方形,
∴∠ABC=90°,AB=BC,BD为对角线,∠DBC=45°。
∵FE⊥AB,
∴∠FEB=90°=∠EBC,EF//BC。
∴∠BCF=∠CFE。
∵BF=AB=BC,
∴∠BFC=∠BCF。
∴∠BCF=∠BFC=∠CFE=$\frac {1}{2}$∠EFB=15°。
∴∠DOC=∠DBC+∠BCF=45°+15°=60°。
答案:60°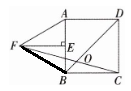
解:连结BF。
∵E为AB中点,
∴AB=2AE。
∵AF=2AE,
∴AB=AF。
∵FE⊥AB,E为AB中点,
∴AF=BF。
∴AF=AB=BF,△ABF为等边三角形,∠AFB=60°。
∵AF=FB,EF⊥AB,
∴∠AFE=∠EFB=30°。
∵四边形ABCD为正方形,
∴∠ABC=90°,AB=BC,BD为对角线,∠DBC=45°。
∵FE⊥AB,
∴∠FEB=90°=∠EBC,EF//BC。
∴∠BCF=∠CFE。
∵BF=AB=BC,
∴∠BFC=∠BCF。
∴∠BCF=∠BFC=∠CFE=$\frac {1}{2}$∠EFB=15°。
∴∠DOC=∠DBC+∠BCF=45°+15°=60°。
答案:60°

14. 如图,P是正方形ABCD内一点,连结PA,PB,PC.若PA= $2\sqrt{3}$,PB= $\sqrt{2}$,∠APB= 135°,则PC的长是______.

答案:
解:过点 $ B $ 向右上作 $ BF \perp BP $,在 $ BF $ 上截取 $ BE = BP $,连结 $ CE $。
因为四边形 $ ABCD $ 是正方形,所以 $ AB = BC $,$ \angle ABC = 90^{\circ} $。
又因为 $ BF \perp BP $,所以 $ \angle PBE = 90^{\circ} $,则 $ \angle ABP + \angle PBC = \angle PBC + \angle CBE $,即 $ \angle ABP = \angle CBE $。
在 $ \triangle APB $ 和 $ \triangle CEB $ 中,$\begin{cases} AB = BC \\ \angle ABP = \angle CBE \\ BP = BE \end{cases}$,所以 $ \triangle APB \cong \triangle CEB $(SAS)。
因此,$ BP = BE = \sqrt{2} $,$ AP = CE = 2\sqrt{3} $,$ \angle APB = \angle CEB = 135^{\circ} $。
连结 $ PE $,因为 $ BP = BE $ 且 $ \angle PBE = 90^{\circ} $,所以 $ \triangle PBE $ 为等腰直角三角形。
由勾股定理,得 $ PE = \sqrt{BP^{2} + BE^{2}} = \sqrt{(\sqrt{2})^{2} + (\sqrt{2})^{2}} = 2 $,且 $ \angle PEB = 45^{\circ} $。
所以 $ \angle PEC = \angle CEB - \angle PEB = 135^{\circ} - 45^{\circ} = 90^{\circ} $。
在 $ Rt\triangle PEC $ 中,由勾股定理,得 $ PC = \sqrt{PE^{2} + CE^{2}} = \sqrt{2^{2} + (2\sqrt{3})^{2}} = \sqrt{4 + 12} = \sqrt{16} = 4 $。
故 $ PC $ 的长是 $ 4 $。
解:过点 $ B $ 向右上作 $ BF \perp BP $,在 $ BF $ 上截取 $ BE = BP $,连结 $ CE $。
因为四边形 $ ABCD $ 是正方形,所以 $ AB = BC $,$ \angle ABC = 90^{\circ} $。
又因为 $ BF \perp BP $,所以 $ \angle PBE = 90^{\circ} $,则 $ \angle ABP + \angle PBC = \angle PBC + \angle CBE $,即 $ \angle ABP = \angle CBE $。
在 $ \triangle APB $ 和 $ \triangle CEB $ 中,$\begin{cases} AB = BC \\ \angle ABP = \angle CBE \\ BP = BE \end{cases}$,所以 $ \triangle APB \cong \triangle CEB $(SAS)。
因此,$ BP = BE = \sqrt{2} $,$ AP = CE = 2\sqrt{3} $,$ \angle APB = \angle CEB = 135^{\circ} $。
连结 $ PE $,因为 $ BP = BE $ 且 $ \angle PBE = 90^{\circ} $,所以 $ \triangle PBE $ 为等腰直角三角形。
由勾股定理,得 $ PE = \sqrt{BP^{2} + BE^{2}} = \sqrt{(\sqrt{2})^{2} + (\sqrt{2})^{2}} = 2 $,且 $ \angle PEB = 45^{\circ} $。
所以 $ \angle PEC = \angle CEB - \angle PEB = 135^{\circ} - 45^{\circ} = 90^{\circ} $。
在 $ Rt\triangle PEC $ 中,由勾股定理,得 $ PC = \sqrt{PE^{2} + CE^{2}} = \sqrt{2^{2} + (2\sqrt{3})^{2}} = \sqrt{4 + 12} = \sqrt{16} = 4 $。
故 $ PC $ 的长是 $ 4 $。
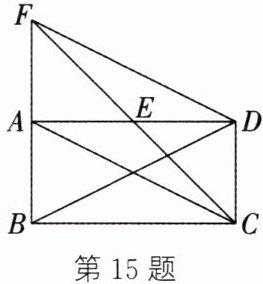
15. (10分)如图,在矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连结AC,BD,DF.
(1)求证:BD= DF;
(2)当CF平分∠BCD,且BC= 6时,求CD的长.
(1)求证:BD= DF;
(2)当CF平分∠BCD,且BC= 6时,求CD的长.

答案:
(1) 证明:
∵ 四边形 $ABCD$ 是矩形,
∴ $AB // CD$,$AC = BD$,$\angle FAE = \angle CDE$。
∵ $E$ 是 $AD$ 的中点,
∴ $AE = DE$。
在 $\triangle FAE$ 和 $\triangle CDE$ 中,
$\begin{cases} \angle FAE = \angle CDE, \\ AE = DE, \\ \angle FEA = \angle CED, \end{cases}$
∴ $\triangle FAE \cong \triangle CDE$(ASA)。
∴ $FA = CD$。
又
∵ $AF // CD$,
∴ 四边形 $ACDF$ 是平行四边形。
∴ $DF = AC$。
∵ $AC = BD$,
∴ $BD = DF$。
(2) 解:
∵ 四边形 $ABCD$ 是矩形,
∴ $AD = BC = 6$,$\angle BCD = \angle CDE = 90^\circ$。
∵ $CF$ 平分 $\angle BCD$,
∴ $\angle DCE = 45^\circ$。
在 $\triangle CDE$ 中,$\angle CDE = 90^\circ$,
∴ $\angle DEC = 180^\circ - 90^\circ - 45^\circ = 45^\circ$。
∴ $\angle DEC = \angle DCE$,
∴ $CD = DE$。
∵ $E$ 是 $AD$ 的中点,
∴ $DE = \frac{1}{2}AD = \frac{1}{2} × 6 = 3$。
∴ $CD = 3$。
(1) 证明:
∵ 四边形 $ABCD$ 是矩形,
∴ $AB // CD$,$AC = BD$,$\angle FAE = \angle CDE$。
∵ $E$ 是 $AD$ 的中点,
∴ $AE = DE$。
在 $\triangle FAE$ 和 $\triangle CDE$ 中,
$\begin{cases} \angle FAE = \angle CDE, \\ AE = DE, \\ \angle FEA = \angle CED, \end{cases}$
∴ $\triangle FAE \cong \triangle CDE$(ASA)。
∴ $FA = CD$。
又
∵ $AF // CD$,
∴ 四边形 $ACDF$ 是平行四边形。
∴ $DF = AC$。
∵ $AC = BD$,
∴ $BD = DF$。
(2) 解:
∵ 四边形 $ABCD$ 是矩形,
∴ $AD = BC = 6$,$\angle BCD = \angle CDE = 90^\circ$。
∵ $CF$ 平分 $\angle BCD$,
∴ $\angle DCE = 45^\circ$。
在 $\triangle CDE$ 中,$\angle CDE = 90^\circ$,
∴ $\angle DEC = 180^\circ - 90^\circ - 45^\circ = 45^\circ$。
∴ $\angle DEC = \angle DCE$,
∴ $CD = DE$。
∵ $E$ 是 $AD$ 的中点,
∴ $DE = \frac{1}{2}AD = \frac{1}{2} × 6 = 3$。
∴ $CD = 3$。
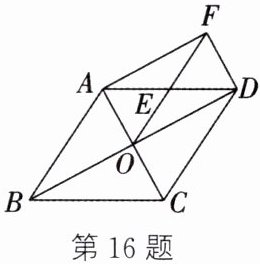
16. (10分)(遂宁中考)如图,在菱形ABCD中,对角线AC,BD相交于点O,E是AD的中点,连结OE,过点D作DF//AC,交OE的延长线于点F,连结AF.
(1)求证:△AOE≌△DFE;
(2)判断四边形AODF的形状,并说明理由.
(1)求证:△AOE≌△DFE;
(2)判断四边形AODF的形状,并说明理由.

答案:
(1) 证明:
∵ E 是 AD 的中点,
∴ AE = DE。
∵ DF // AC,
∴ ∠OAE = ∠FDE。
在△AOE 和△DFE 中,
∠OAE = ∠FDE,
AE = DE,
∠AEO = ∠DEF,
∴ △AOE ≌ △DFE(ASA)。
(2) 四边形 AODF 是矩形。
理由:
∵ △AOE ≌ △DFE,
∴ AO = DF。
∵ DF // AC,
∴ 四边形 AODF 是平行四边形。
∵ 四边形 ABCD 是菱形,
∴ AC ⊥ BD,即 ∠AOD = 90°。
∴ 四边形 AODF 是矩形。
(1) 证明:
∵ E 是 AD 的中点,
∴ AE = DE。
∵ DF // AC,
∴ ∠OAE = ∠FDE。
在△AOE 和△DFE 中,
∠OAE = ∠FDE,
AE = DE,
∠AEO = ∠DEF,
∴ △AOE ≌ △DFE(ASA)。
(2) 四边形 AODF 是矩形。
理由:
∵ △AOE ≌ △DFE,
∴ AO = DF。
∵ DF // AC,
∴ 四边形 AODF 是平行四边形。
∵ 四边形 ABCD 是菱形,
∴ AC ⊥ BD,即 ∠AOD = 90°。
∴ 四边形 AODF 是矩形。
查看更多完整答案,请扫码查看


