《2025年暑期升级训练八年级数学浙教版浙江教育出版社》

9. 如图,直线$y= -\frac{1}{2}x+2与x轴交于点B$,与$y轴交于点A$。过线段$AB的中点A_{1}作A_{1}B_{1}\perp x轴于点B_{1}$,连结$OA_{1}$；过线段$A_{1}B的中点A_{2}作A_{2}B_{2}\perp x轴于点B_{2}$,连结$B_{1}A_{2}$；过线段$A_{2}B的中点A_{3}作A_{3}B_{3}\perp x轴于点B_{3}$,连结$B_{2}A_{3}$……依此类推,$\triangle A_{n}B_{n}B_{n-1}(n\geqslant 2)$的面积为(C)
A.$\frac{1}{2^{n-1}}$
B.$\frac{1}{2^{n}}$
C.$\frac{1}{4^{n-1}}$
D.$\frac{1}{4^{n}}$

答案： C　解析:
∵直线$y = -\frac {1}{2}x+2$与x轴交于点B,与y轴交于点A,
∴易得A(0,2),B(4,0).
∴OA = 2,OB = 4.
∴△AOB的面积为$\frac {1}{2}×2×4 = 4$.易知$OB_{1}=B_{1}B=\frac {1}{2}OB = 2$,$A_{1}B_{1}=\frac {1}{2}OA = 1$,
∴△$A_{1}B_{1}O$的面积为$\frac {1}{2}×2×1 = 1$.同理,可得△$A_{2}B_{2}B_{1}$的面积为$\frac {1}{4}$,△$A_{3}B_{3}B_{2}$的面积为$\frac {1}{16}$……
∴△$A_{n}B_{n}B_{n - 1}(n\geq2)$的面积为$\frac {1}{4^{n - 1}}$.

10. 如图,在平面直角坐标系中,菱形$ABCD与菱形GFED关于点D$成中心对称,点$C$,$G在x$轴的正半轴上,点$A$,$F在反比例函数y= \frac{k}{x}(k＞0,x＞0)$的图象上,延长$AB交x轴于点P(1,0)$。若$\angle APO= 120^{\circ}$,则$k$的值是( )

A.3
B.$3\sqrt{3}$
C.6
D.$6\sqrt{3}$

答案：
D解析:
∵菱形ABCD与菱形GFED关于点D成中心对称,∠APO = 120°,
∴AP//CE//FG,AG//BC,∠APG = 60°,DC = DG.
∴∠APG = ∠DCG = ∠DGC = 60°.
∴∠BCP = ∠DGC = 60°.
∴易得△BPC,△APG和△CDG都是等边三角形.
∴BP = BC = PC = CD = CG.如图,过点F作FH⊥x轴于点H,连结AC,BF,则易得AC⊥x轴,BF//x轴.设菱形ABCD和菱形GFED的边长为$a(a＞0)$,则AP = 2a,PC = CG = a.
∴$AC=\sqrt {AP^{2}-PC^{2}}=\sqrt {3}a$.
∵AP//FG,
∴∠FGH = ∠APG = 60°.
∴在Rt△FGH中,∠GFH = 90°−∠FGH = 30°.
∴易得$GH=\frac {1}{2}a$,$FH=\frac {\sqrt {3}}{2}a$.
∵点P的坐标为(1,0),
∴点A的坐标为$(a + 1,\sqrt {3}a)$,点F的坐标为$(1 + a + a+\frac {1}{2}a,\frac {\sqrt {3}}{2}a)$.
∵点A,F在反比例函数$y=\frac {k}{x}(k＞0,x＞0)$的图象上,
∴$\sqrt {3}a(a + 1)=\frac {\sqrt {3}}{2}a(1+\frac {5}{2}a)$,解得$a_{1}=0$,$a_{2}=2$.
∵$a＞0$,
∴$a = 2$.
∴点A的坐标为$(3,2\sqrt {3})$.
∴$k = 3×2\sqrt {3}=6\sqrt {3}$
　　　　　　　

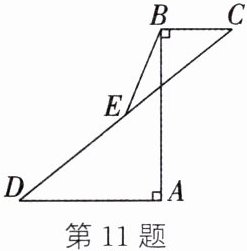
11. (鄂尔多斯中考)如图,$AB\perp BC于点B$,$AB\perp AD于点A$,$E是CD$的中点。若$BC= 5$,$AD= 10$,$BE= \frac{13}{2}$,则$AB$的长是______。

答案：
解：延长BE交AD于点F。
∵E是CD的中点，
∴DE=CE。
∵AB⊥BC，AB⊥AD，
∴AD//BC。
∴∠D=∠C。
又
∵∠FED=∠BEC，
∴△FDE≌△BCE（ASA）。
∴DF=CB=5，FE=BE。
∵BE=$\frac {13}{2}$，
∴BF=2BE=13。
∵AD=10，
∴AF=AD-DF=10-5=5。
在Rt△ABF中，由勾股定理得：
AB=$\sqrt {(BF²-AF²)}=\sqrt {(13²-5²)}=\sqrt {(169-25)}$=12。
故AB的长是12。

12. 若某等腰三角形的两边长$a$,$b满足a^{2}+b^{2}-6a-14b+58= 0$,则这个等腰三角形的周长为______17。

答案： 解：将等式变形为$(a^{2}-6a + 9)+(b^{2}-14b + 49)=0$，即$(a - 3)^{2}+(b - 7)^{2}=0$。
∵$(a - 3)^{2}\geq0$，$(b - 7)^{2}\geq0$，
∴$a - 3 = 0$，$b - 7 = 0$，解得$a = 3$，$b = 7$。
情况一：当3是腰长时，三边长分别为3，3，7。
∵$3 + 3 = 6\lt7$，不符合三角形三边关系，舍去。
情况二：当3是底边长时，三边长分别为3，7，7。
∵$3 + 7 = 10\gt7$，符合三角形三边关系。
周长为$3 + 7 + 7 = 17$。
故这个等腰三角形的周长为17。

13. (达州中考)已知关于$x的不等式组\begin{cases}-x+a＜2,\frac{3x-1}{2}\leqslant x+1\end{cases} $恰有3个整数解,则$a$的取值范围是______$2\leq a＜3$。

答案： 解：记不等式组为$\begin{cases}-x + a＜2①\\frac{3x - 1}{2}\leq x + 1②\end{cases}$
解不等式①：$-x + a＜2$，移项得$-x＜2 - a$，两边同乘$-1$（不等号变向）得$x＞a - 2$；
解不等式②：$\frac{3x - 1}{2}\leq x + 1$，两边同乘$2$得$3x - 1\leq 2x + 2$，移项得$3x - 2x\leq 2 + 1$，解得$x\leq3$；
∴不等式组的解集为$a - 2＜x\leq3$；
∵不等式组恰有3个整数解，
∴整数解为1，2，3，
∴$0\leq a - 2＜1$，
解得$2\leq a＜3$。
$2\leq a＜3$

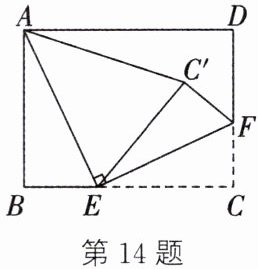
14. (盐城中考)如图,在矩形$ABCD$中,$AB= 3$,$AD= 4$,$E$,$F分别是边BC$,$CD$上的点,$EF\perp AE$,将$\triangle ECF沿EF翻折得到\triangle EC'F$,连结$AC'$。当$BE= $$\frac{7}{8}$或$\frac{4}{3}$时,$\triangle AEC'是以AE$为腰的等腰三角形。

答案： 解：设$BE = x$，则$EC = 4 - x$。由翻折得$EC' = EC = 4 - x$。
情况一：当$AE = EC'$时
$AE = 4 - x$。
在矩形$ABCD$中，$\angle B = 90^\circ$，由勾股定理得：
$AB^2 + BE^2 = AE^2$，即$3^2 + x^2 = (4 - x)^2$。
解得$x = \frac{7}{8}$，$\therefore BE = \frac{7}{8}$。
情况二：当$AE = AC'$时
过点$A$作$AH \perp EC'$于点$H$，则$\angle AHE = 90^\circ$。
$\because EF \perp AE$，$\therefore \angle AEF = 90^\circ$，即$\angle AEC' + \angle FEC' = 90^\circ$。
又$\angle AEB + \angle FEC = 90^\circ$，由翻折得$\angle FEC' = \angle FEC$，$\therefore \angle AEC' = \angle AEB$。
$\because \angle AHE = \angle B = 90^\circ$，$AE = AE$，$\therefore \triangle AHE \cong \triangle ABE$。
$\therefore HE = BE = x$。
$\because AE = AC'$，$AH \perp EC'$，$\therefore EC' = 2HE$，即$4 - x = 2x$。
解得$x = \frac{4}{3}$，$\therefore BE = \frac{4}{3}$。
综上所述，$BE = \frac{7}{8}$或$\frac{4}{3}$。
答案：$\frac{7}{8}$或$\frac{4}{3}$

15. (葫芦岛中考)如图,直线$y= 2x+4与x轴交于点A$,与$y轴交于点B$,$D为OB$的中点,$□ OCDE的顶点C在x$轴上,顶点$E在直线AB$上,则$□ OCDE$的面积为______。

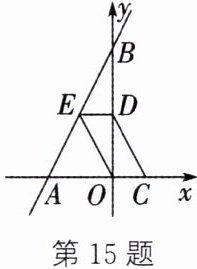
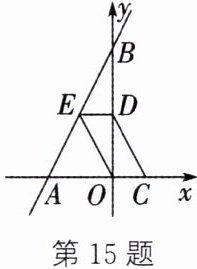
2

答案： 解：当$x = 0$时，$y = 2×0 + 4 = 4$，则点$B$的坐标为$(0,4)$，$OB = 4$。
因为$D$为$OB$的中点，所以$OD=\frac{1}{2}OB=\frac{1}{2}×4 = 2$。
由于四边形$OCDE$为平行四边形，且点$C$在$x$轴上，所以$DE// x$轴，$DE = OC$。
当$y = 2$时，$2x + 4 = 2$，解得$x=-1$，则点$E$的坐标为$(-1,2)$，$DE = 1$，故$OC = 1$。
因此，▱$OCDE$的面积为$OC\cdot OD=1×2 = 2$。
2

16. (玉林中考)如图,点$A在反比例函数y= \frac{k}{x}(k＞0,x＞0)$的图象上,点$B在直线l:y= mx-2b(m＞0,b＞0)$上,点$A$,$B关于x$轴对称,直线$l与y轴交于点C$。当四边形$AOCB$是菱形时,有下列结论：①$A(b,\sqrt{3}b)$；②当$b= 2$时,$k= 4\sqrt{3}$；③$m= \frac{\sqrt{3}}{3}$；④$S_{四边形AOCB}= 2b^{2}$。其中,正确的是______②③(填序号)。

答案： 解：令AB与x轴交于点D。
在$y=mx-2b$中，当$x=0$时，$y=-2b$，$\therefore C(0,-2b)$，$\therefore OC=2b$。
∵四边形AOCB是菱形，$\therefore AB=OC=OA=2b$。
∵点A，B关于x轴对称，$\therefore AB\perp OD$，$AD=BD=b$。
$\therefore OD=\sqrt{(2b)^2 - b^2}=\sqrt{3}b$，$\therefore A(\sqrt{3}b,b)$，故①不正确。
当$b=2$时，$A(2\sqrt{3},2)$，$\because$点A在$y=\frac{k}{x}$上，$\therefore k=2\sqrt{3}×2=4\sqrt{3}$，故②正确。
$\because A(\sqrt{3}b,b)$，点A，B关于x轴对称，$\therefore B(\sqrt{3}b,-b)$。
∵点B在直线$l$上，$\therefore \sqrt{3}bm - 2b=-b$，解得$m=\frac{\sqrt{3}}{3}$，故③正确。
$S_{四边形AOCB}=AB\cdot OD=2b\cdot\sqrt{3}b=2\sqrt{3}b^2$，故④不正确。
综上，正确的是②③。

17. (8分)定义：若两个二次根式$a$,$b满足ab= c$,且$c$是有理数,则称$a与b是关于c$的“共轭二次根式”。
(1)若$a与\sqrt{2}$是关于4的“共轭二次根式”,则$a= $$2\sqrt{2}$；
(2)若$\sqrt{m-2}与\sqrt{\frac{m}{4}-2}$是关于2的“共轭二次根式”,求$m$的值。
由题意，得$m - 2\geq0$，$\frac{m}{4}-2\geq0$，∴$m\geq8$。∵$\sqrt{m - 2}$与$\sqrt{\frac{m}{4}-2}$是关于2的“共轭二次根式”，∴$\sqrt{m - 2}\cdot\sqrt{\frac{m}{4}-2}=2$。∴$(m - 2)(m - 8)=16$。∴$m^2 - 10m = 0$，解得$m = 10$或$m = 0$（不合题意，舍去）。∴$m$的值为10。

答案：
(1)$2\sqrt {2}$. 解析:
∵a与$\sqrt {2}$是关于4的“共轭二次根式”,
∴$\sqrt {2}a = 4$.
∴$a=\frac {4}{\sqrt {2}}=2\sqrt {2}$
(2)由题意,得$m - 2\geq0$,$\frac {m}{4}-2\geq0$,
∴$m\geq8$.
∵$\sqrt {m - 2}$与$\sqrt {\frac {m}{4}-2}$是关于2的“共轭二次根式”,
∴$\sqrt {m - 2}\cdot\sqrt {\frac {m}{4}-2}=2$.
∴$(m - 2)(m - 8)=16$.
∴$m^{2}-10m = 0$,解得$m = 10$或$m = 0$(不合题意，舍去).
∴m的值为10.