《2025年暑期升级训练八年级数学浙教版浙江教育出版社》

4. 如图,在$△ABC$中,$BE是∠ABC$的平分线,$AD⊥BE$,垂足为$D$. 求证：$∠2= ∠1+∠C$.

答案：
如图, 延长AD交BC于点F. $\because BE$是$∠ABC$的平分线,$\therefore ∠ABD=∠FBD$. $\because BD⊥AD,$$\therefore ∠ADB=∠FDB=90^{\circ }$. 在$\triangle ABD$和$\triangle FBD$中,$\because \left\{\begin{array}{l} ∠ABD=∠FBD,\\ BD=BD,\\ ∠ADB=∠FDB,\end{array}\right. $$\therefore \triangle ABD\cong \triangle FBD.$$\therefore ∠2=∠DFB$. $\because ∠DFB=∠1+∠C,$$\therefore ∠2=∠1+∠C$.

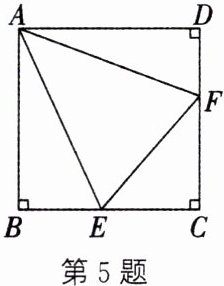
5. 如图,在四边形$ABCD$中,$∠ABC= ∠C= ∠D= 90^{\circ}$,$AB= AD$,$E为BC$上的一点,$F为CD$上的一点,$BE+DF= EF$,求$∠EAF$的度数.

答案：
$\because ∠ABC=∠C=∠D=90^{\circ },$$\therefore ∠BAD=90^{\circ }$. 如图, 延长CB到点H, 使得$BH=DF$, 连结AH. $\because ∠ABE=90^{\circ },$$\therefore ∠ABH=∠D=90^{\circ }$. 在$\triangle ABH$和$\triangle ADF$中,$\because \left\{\begin{array}{l} AB=AD,\\ ∠ABH=∠D,\\ BH=DF,\end{array}\right. $$\therefore \triangle ABH\cong \triangle ADF.$$\therefore AH=AF,∠BAH=∠DAF.$$\therefore ∠BAH+∠BAF=∠DAF+∠BAF$, 即$∠HAF=∠BAD=90^{\circ }.$$\because BE+DF=EF,$$\therefore BE+BH=EF$, 即$EH=EF$. 在$\triangle AEH$和$\triangle AEF$中,$\because \left\{\begin{array}{l} AH=AF,\\ AE=AE,\\ EH=EF,\end{array}\right. $$\therefore \triangle AEH\cong \triangle AEF.$$\therefore ∠EAH=∠EAF.$$\therefore ∠EAF=\frac {1}{2}∠HAF=45^{\circ }$.

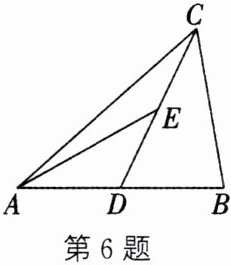
6. 如图,在$△ABC$中,$D是AB$的中点,$E是边DC$上的一点,且$AE= BC$. 求证：$∠DEA= ∠BCD$.

答案：
如图, 延长CD至点F, 使$DF=DC$, 连结AF. $\because D$是AB的中点, $\therefore DA=DB$. 在$\triangle DAF$和$\triangle DBC$中,$\because \left\{\begin{array}{l} DF=DC,\\ ∠ADF=∠BDC,\\ DA=DB,\end{array}\right. $$\triangle DAF\cong \triangle DBC.$$\therefore ∠F=∠BCD,AF=BC.$$\because AE=BC,$$\therefore AE=AF.$$\therefore ∠F=∠DEA.$$\therefore ∠DEA=∠BCD$.

7. 如图,$AB= AE$,$AB⊥AE$,$AD= AC$,$AD⊥AC$,$M为BC$的中点. 求证：$DE= 2AM$.

答案：
如图, 延长AM至点N, 使$NM=AM$, 连结BN. $\because M$为BC的中点, $\therefore BM=CM$. 在$\triangle AMC$和$\triangle NMB$中,$\because AM=NM,∠AMC=∠NMB,CM=BM,$$\therefore \triangle AMC\cong \triangle NMB.$$\therefore AC=NB,∠C=∠NBM.$$\therefore ∠ABN=∠ABC+∠NBM=∠ABC+∠C=180^{\circ }-∠BAC$. $\because AB⊥AE,AD⊥AC,$$\therefore ∠BAE=∠CAD=90^{\circ }$. $\therefore ∠EAD=360^{\circ }-∠BAE-∠CAD-∠BAC=180^{\circ }-∠BAC.$$\therefore ∠ABN=∠EAD.$$\because AD=AC,$$\therefore AD=BN$. 在$\triangle ABN$和$\triangle EAD$中,$\because BN=AD,∠ABN=∠EAD,AB=EA,$$\therefore \triangle ABN\cong \triangle EAD.$$\therefore NA=DE.$$\therefore DE=2AM$.

方法点金：运用倍长中线法解决与中线有关的问题。如果图中给出的已知条件中的线段或角的位置相对比较分散, 而三角形又给出了中线, 我们可以倍长这条中线, 使得分散的条件在图形中能够相对集中, 再运用其中的线段、角之间隐含的关系解决问题。