《2025年暑期升级训练八年级数学浙教版浙江教育出版社》

12. 若实数m,n满足$|m-3|+\sqrt {n-4}= 0$,且m,n恰好是$Rt△ABC$的两条边长,则$△ABC$的周长是 (A)
A.12或$7+\sqrt {7}$
B.5
C.12
D.5或$\sqrt {7}$

答案： A　解析:根据题意，得$|m - 3| = 0$，$\sqrt{n - 4} = 0$，
∴$m = 3$，$n = 4$。当 4 是直角边长时，斜边长$=\sqrt{3^{2}+4^{2}}=5$。
∴$\triangle ABC$的周长$=3 + 4 + 5 = 12$。当 4 是斜边长时，另一条直角边长$=\sqrt{4^{2}-3^{2}}=\sqrt{7}$。
∴$\triangle ABC$的周长$=3 + 4 + \sqrt{7} = 7 + \sqrt{7}$。综上所述，$\triangle ABC$的周长是 12 或$7 + \sqrt{7}$。

13. 在$△ABC$中,$AB= BC= 2$,O是线段AB的中点,P是射线CO上的一个动点,$∠AOC= 60^{\circ }$.当$△PAB$为直角三角形时,AP的长为 ( )

A.1或$\sqrt {3}$或7
B.1或$\sqrt {5}或\sqrt {7}$
C.1或$\sqrt {3}或\sqrt {7}$
D.1或3或$\sqrt {7}$

答案：
C　解析:
∵$AB = 2$，O是线段AB的中点，
∴$OA = OB = 1$。分三种情况讨论:①如图①，当点P在CO的延长线上，且$\angle APB = 90^{\circ}$时，由直角三角形斜边上的中线等于斜边的一半，可得$OP=\frac{1}{2}AB = OB$。
∵$\angle AOC=\angle BOP = 60^{\circ}$，
∴$\triangle OBP$为等边三角形。
∴$BP = OB = 1$。在$Rt\triangle ABP$中，由勾股定理，得$AP=\sqrt{AB^{2}-BP^{2}}=\sqrt{3}$。②如图②，当$\angle ABP = 90^{\circ}$时，
∵$\angle AOC=\angle BOP = 60^{\circ}$，
∴$\angle OPB = 30^{\circ}$。
∴易得$OP = 2OB = 2$。在$Rt\triangle OBP$中，由勾股定理，得$BP=\sqrt{OP^{2}-OB^{2}}=\sqrt{3}$。在$Rt\triangle ABP$中，由勾股定理，得$AP=\sqrt{AB^{2}+BP^{2}}=\sqrt{7}$。③如图③，当点P在线段OC上，且$\angle APB = 90^{\circ}$时，$OP=\frac{1}{2}AB = OA$。
∵$\angle AOC = 60^{\circ}$，
∴$\triangle AOP$是等边三角形。
∴$AP = OA = 1$。综上所述，AP的长为$\sqrt{3}$或$\sqrt{7}$或 1。

14. 如图,$∠AOB= 50^{\circ }$,P是边OB上的一个动点(不与点O重合),当$∠A$的度数为90°或40°时,$△AOP$为直角三角形.

答案： 解：分两种情况讨论：
1. 当∠A=90°时，△AOP为直角三角形；
2. 当∠APO=90°时，∠A=180°-∠AOB-∠APO=180°-50°-90°=40°，此时△AOP为直角三角形。
综上，∠A的度数为90°或40°。

15. 如图,在$Rt△ABC$中,$∠ABC= 90^{\circ },AB= 20,BC= 15$,D为边AC上的动点,点D从点C出发,以每秒2个单位的速度沿边CA往点A运动,当运动到点A时停止运动.设点D运动的时间为t秒.若$△CBD$是直角三角形,求t的值.

答案： 解：由题意，得$CD=2t$。
$\because \angle ABC=90^{\circ}$，$AB=20$，$BC=15$，
$\therefore AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{20^{2}+15^{2}}=25$。
分两种情况讨论：
①当$\angle CDB=90^{\circ}$时，
$S_{\triangle ABC}=\frac{1}{2}AC\cdot BD=\frac{1}{2}AB\cdot BC$，
即$\frac{1}{2}×25BD=\frac{1}{2}×20×15$，解得$BD=12$。
$\therefore CD=\sqrt{BC^{2}-BD^{2}}=\sqrt{15^{2}-12^{2}}=9$。
$\therefore 2t=9$，解得$t=4.5$。
②当$\angle CBD=90^{\circ}$时，
点$D$与点$A$重合，此时$CD=AC=25$。
$\therefore 2t=25$，解得$t=12.5$。
综上所述，$t=4.5$或$12.5$。

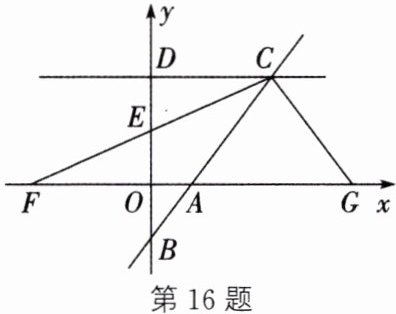
16. 如图,在平面直角坐标系中,过点$A(3,0),C(9,8)$的直线AC交y轴于点B,过点C作平行于x轴的直线CD交y轴于点D,点$E(0,t)$在线段OD上,连结CE并延长,交x轴于点F,点G在x轴的正半轴上,且$AG= AF$,连结CG.
(1) 求直线AC对应的函数表达式.
(2) 当E恰好是OD的中点时,求$△ACG$的面积.
(3) 是否存在t,使得$△FCG$是直角三角形? 若存在,请写出t的值;若不存在,请说明理由.

答案：
(1)设直线AC对应的函数表达式为$y=kx+b$，将$A(3,0)$，$C(9,8)$代入，得$\begin{cases}3k+b=0\\9k+b=8\end{cases}$，解得$\begin{cases}k=\frac{4}{3}\\b=-4\end{cases}$，
∴直线AC对应的函数表达式为$y=\frac{4}{3}x-4$。
(2)
∵点$C(9,8)$，$CD// x$轴，
∴$D(0,8)$，$CD=9$。
∵E是OD中点，
∴$DE=OE$。
∵$CD// x$轴，
∴$\angle DCE=\angle OFE$，$\angle CDE=\angle FOE$，
∴$\triangle EDC\cong\triangle EOF$，
∴$FO=CD=9$。
∵$A(3,0)$，
∴$OA=3$，$AG=AF=FO+OA=12$。过点C作$CH\perp x$轴于H，$CH=8$，
∴$S_{\triangle ACG}=\frac{1}{2}×12×8=48$。
(3)存在。
①当$\angle FCG=90^{\circ}$时，
∵$AG=AF$，
∴AC是$Rt\triangle FCG$斜边FG上的中线，
∴$AF=AC$。过点C作$CM\perp x$轴于M，$CM=8$，$AM=9-3=6$，$AC=\sqrt{6^{2}+8^{2}}=10$，
∴$AF=10$，$F(-7,0)$。设直线CF：$y=mx+n$，将$(9,8)$，$(-7,0)$代入，得$\begin{cases}9m+n=8\\-7m+n=0\end{cases}$，解得$\begin{cases}m=\frac{1}{2}\\n=\frac{7}{2}\end{cases}$，
∴$y=\frac{1}{2}x+\frac{7}{2}$，令$x=0$，$y=\frac{7}{2}$，
∴$t=\frac{7}{2}$。
②当$\angle CGF=90^{\circ}$时，$G(9,0)$，$AG=9-3=6$，$AF=6$，$F(-3,0)$。设直线CF：$y=mx+n$，将$(9,8)$，$(-3,0)$代入，得$\begin{cases}9m+n=8\\-3m+n=0\end{cases}$，解得$\begin{cases}m=\frac{2}{3}\\n=2\end{cases}$，
∴$y=\frac{2}{3}x+2$，令$x=0$，$y=2$，
∴$t=2$。
综上，$t=\frac{7}{2}$或$2$。