第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
15. 若$x= \frac {\sqrt {5}+1}{2}$,则$\frac {x^{2}-x+1+2\sqrt {3}}{(x^{2}-x)^{2}+2+\sqrt {3}}$的值为(
A.$\frac {2\sqrt {3}}{3}$
B.$\frac {\sqrt {3}}{3}$
C.$\sqrt {3}$
D.$\sqrt {3}或\frac {\sqrt {3}}{3}$
A
)A.$\frac {2\sqrt {3}}{3}$
B.$\frac {\sqrt {3}}{3}$
C.$\sqrt {3}$
D.$\sqrt {3}或\frac {\sqrt {3}}{3}$
答案:
A 解析:
∵ $x = \frac{\sqrt{5} + 1}{2}$,
∴ $x^2 - x = x(x - 1) = \frac{\sqrt{5} + 1}{2} × (\frac{\sqrt{5} + 1}{2} - 1) = \frac{\sqrt{5} + 1}{2} × \frac{\sqrt{5} - 1}{2} = 1$.
∴ $\frac{x^2 - x + 1 + 2\sqrt{3}}{(x^2 - x)^2 + 2 + \sqrt{3}} = \frac{1 + 1 + 2\sqrt{3}}{1^2 + 2 + \sqrt{3}} = \frac{2 + 2\sqrt{3}}{3 + \sqrt{3}} = \frac{(2 + 2\sqrt{3}) × (3 - \sqrt{3})}{(3 + \sqrt{3}) × (3 - \sqrt{3})} = \frac{2\sqrt{3}}{3}$.
∵ $x = \frac{\sqrt{5} + 1}{2}$,
∴ $x^2 - x = x(x - 1) = \frac{\sqrt{5} + 1}{2} × (\frac{\sqrt{5} + 1}{2} - 1) = \frac{\sqrt{5} + 1}{2} × \frac{\sqrt{5} - 1}{2} = 1$.
∴ $\frac{x^2 - x + 1 + 2\sqrt{3}}{(x^2 - x)^2 + 2 + \sqrt{3}} = \frac{1 + 1 + 2\sqrt{3}}{1^2 + 2 + \sqrt{3}} = \frac{2 + 2\sqrt{3}}{3 + \sqrt{3}} = \frac{(2 + 2\sqrt{3}) × (3 - \sqrt{3})}{(3 + \sqrt{3}) × (3 - \sqrt{3})} = \frac{2\sqrt{3}}{3}$.
16. 已知$a= \sqrt {2}-1$,求代数式$2(a+\sqrt {3})(a-\sqrt {3})-a(a-2)+7$的值。
答案:
解:原式$=2(a^2 - 3) - a(a - 2) + 7$
$=2a^2 - 6 - a^2 + 2a + 7$
$=a^2 + 2a + 1$
$=(a + 1)^2$
当$a = \sqrt{2} - 1$时,
原式$=(\sqrt{2} - 1 + 1)^2$
$=(\sqrt{2})^2$
$=2$
$=2a^2 - 6 - a^2 + 2a + 7$
$=a^2 + 2a + 1$
$=(a + 1)^2$
当$a = \sqrt{2} - 1$时,
原式$=(\sqrt{2} - 1 + 1)^2$
$=(\sqrt{2})^2$
$=2$
17. 若m,n均为有理数,且$\sqrt {3}+\sqrt {12}+\sqrt {\frac {3}{4}}= m+n\sqrt {3}$,求$(m-n)^{2}+2n$的值。
答案:
解:
∵$\sqrt{3} + \sqrt{12} + \sqrt{\frac{3}{4}} = m + n\sqrt{3}$,
$\sqrt{3} + \sqrt{12} + \sqrt{\frac{3}{4}} = \sqrt{3} + 2\sqrt{3} + \frac{\sqrt{3}}{2} = \frac{7\sqrt{3}}{2}$,
∴$m = 0$,$n = \frac{7}{2}$.
∴$(m - n)^2 + 2n = (0 - \frac{7}{2})^2 + 2×\frac{7}{2} = \frac{49}{4} + 7 = \frac{77}{4}$.
∵$\sqrt{3} + \sqrt{12} + \sqrt{\frac{3}{4}} = m + n\sqrt{3}$,
$\sqrt{3} + \sqrt{12} + \sqrt{\frac{3}{4}} = \sqrt{3} + 2\sqrt{3} + \frac{\sqrt{3}}{2} = \frac{7\sqrt{3}}{2}$,
∴$m = 0$,$n = \frac{7}{2}$.
∴$(m - n)^2 + 2n = (0 - \frac{7}{2})^2 + 2×\frac{7}{2} = \frac{49}{4} + 7 = \frac{77}{4}$.
18. 先化简,再求值:$(\frac {1}{x+y}+\frac {1}{x-y})÷\frac {1}{xy+y^{2}}$,其中$x= \sqrt {5}+\sqrt {3}$,$y= \sqrt {5}-\sqrt {3}$。
答案:
解:原式$=[\frac{x - y}{(x + y)(x - y)} + \frac{x + y}{(x + y)(x - y)}] ÷ \frac{1}{y(x + y)}$
$=\frac{2x}{(x + y)(x - y)} \cdot y(x + y)$
$=\frac{2xy}{x - y}$.
∵$x = \sqrt{5} + \sqrt{3}$,$y = \sqrt{5} - \sqrt{3}$,
∴$xy = (\sqrt{5} + \sqrt{3})(\sqrt{5} - \sqrt{3}) = 5 - 3 = 2$,
$x - y = (\sqrt{5} + \sqrt{3}) - (\sqrt{5} - \sqrt{3}) = 2\sqrt{3}$.
∴原式$=\frac{2×2}{2\sqrt{3}} = \frac{4}{2\sqrt{3}} = \frac{2\sqrt{3}}{3}$.
$=\frac{2x}{(x + y)(x - y)} \cdot y(x + y)$
$=\frac{2xy}{x - y}$.
∵$x = \sqrt{5} + \sqrt{3}$,$y = \sqrt{5} - \sqrt{3}$,
∴$xy = (\sqrt{5} + \sqrt{3})(\sqrt{5} - \sqrt{3}) = 5 - 3 = 2$,
$x - y = (\sqrt{5} + \sqrt{3}) - (\sqrt{5} - \sqrt{3}) = 2\sqrt{3}$.
∴原式$=\frac{2×2}{2\sqrt{3}} = \frac{4}{2\sqrt{3}} = \frac{2\sqrt{3}}{3}$.
19. 站在竖直高度为h m的地方,看到的最远水平距离是d m,它们近似地符合公式$d= 8\sqrt {\frac {h}{5}}$。若某一登山者从海拔n m处的山底登上海拔2n m的山顶,则他看到的最远水平距离是原来的多少倍?
答案:
设登山者在海拔$n\ \text{m}$的山底看到的最远水平距离为$d_1\ \text{m}$,在海拔$2n\ \text{m}$的山顶看到的最远水平距离为$d_2\ \text{m}$。
由公式$d = 8\sqrt{\frac{h}{5}}$,得:
$d_1=8\sqrt{\frac{n}{5}}$,$d_2 = 8\sqrt{\frac{2n}{5}}$。
则$\frac{d_2}{d_1}=\frac{8\sqrt{\frac{2n}{5}}}{8\sqrt{\frac{n}{5}}}=\sqrt{\frac{2n}{5}\cdot\frac{5}{n}}=\sqrt{2}$。
答:他看到的最远水平距离是原来的$\sqrt{2}$倍。
由公式$d = 8\sqrt{\frac{h}{5}}$,得:
$d_1=8\sqrt{\frac{n}{5}}$,$d_2 = 8\sqrt{\frac{2n}{5}}$。
则$\frac{d_2}{d_1}=\frac{8\sqrt{\frac{2n}{5}}}{8\sqrt{\frac{n}{5}}}=\sqrt{\frac{2n}{5}\cdot\frac{5}{n}}=\sqrt{2}$。
答:他看到的最远水平距离是原来的$\sqrt{2}$倍。
20. 如图,某防洪指挥部发现某江边一处长500m、高10m、背水坡的坡角为$45^{\circ }的防洪大堤坝(CD// AB)$急需加固。经调查论证,防洪指挥部专家组制定的加固方案是沿背水坡面用土石进行加固,并使上底加宽3m,加固后背水坡EF的坡比$i= 1:\sqrt {3}$。
(1)求加固后堤坝下底增加的宽度AF;
(2)完成这项工程需要土石多少立方米(结果保留根号)?
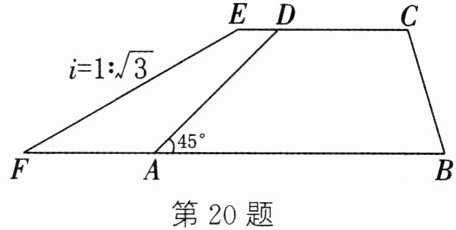
(1)求加固后堤坝下底增加的宽度AF;
(2)完成这项工程需要土石多少立方米(结果保留根号)?

答案:
(1) 分别过点 $ E $,$ D $ 作 $ EG \perp AB $,$ DH \perp AB $,垂足分别为 $ G $,$ H $。
∵ $ CD // AB $,
∴ 四边形 $ DEGH $ 是矩形,
∴ $ EG = DH = 10 \, \text{m} $,$ ED = GH = 3 \, \text{m} $,$ \angle DHA = \angle EGF = 90^\circ $。
∵ $ \angle DAH = 45^\circ $,
∴ $ \triangle ADH $ 是等腰直角三角形,
∴ $ AH = DH = 10 \, \text{m} $。
在 $ \text{Rt}\triangle EFG $ 中,坡比 $ i = 1:\sqrt{3} = \frac{EG}{FG} $,
∴ $ FG = \sqrt{3}EG = 10\sqrt{3} \, \text{m} $。
∴ $ AF = FG + GH - AH = 10\sqrt{3} + 3 - 10 = (10\sqrt{3} - 7) \, \text{m} $。
(2) 加固部分体积 $ = S_{\text{梯形}AFED} × 500 $,
$ S_{\text{梯形}AFED} = \frac{1}{2} × (ED + AF) × EG = \frac{1}{2} × (3 + 10\sqrt{3} - 7) × 10 $,
∴ 体积 $ = \frac{1}{2} × (10\sqrt{3} - 4) × 10 × 500 = (25000\sqrt{3} - 10000) \, \text{m}^3 $。
(1) 加固后堤坝下底增加的宽度 $ AF $ 为 $ (10\sqrt{3} - 7) \, \text{m} $;
(2) 完成这项工程需要土石 $ (25000\sqrt{3} - 10000) \, \text{m}^3 $。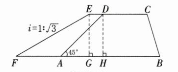
(1) 分别过点 $ E $,$ D $ 作 $ EG \perp AB $,$ DH \perp AB $,垂足分别为 $ G $,$ H $。
∵ $ CD // AB $,
∴ 四边形 $ DEGH $ 是矩形,
∴ $ EG = DH = 10 \, \text{m} $,$ ED = GH = 3 \, \text{m} $,$ \angle DHA = \angle EGF = 90^\circ $。
∵ $ \angle DAH = 45^\circ $,
∴ $ \triangle ADH $ 是等腰直角三角形,
∴ $ AH = DH = 10 \, \text{m} $。
在 $ \text{Rt}\triangle EFG $ 中,坡比 $ i = 1:\sqrt{3} = \frac{EG}{FG} $,
∴ $ FG = \sqrt{3}EG = 10\sqrt{3} \, \text{m} $。
∴ $ AF = FG + GH - AH = 10\sqrt{3} + 3 - 10 = (10\sqrt{3} - 7) \, \text{m} $。
(2) 加固部分体积 $ = S_{\text{梯形}AFED} × 500 $,
$ S_{\text{梯形}AFED} = \frac{1}{2} × (ED + AF) × EG = \frac{1}{2} × (3 + 10\sqrt{3} - 7) × 10 $,
∴ 体积 $ = \frac{1}{2} × (10\sqrt{3} - 4) × 10 × 500 = (25000\sqrt{3} - 10000) \, \text{m}^3 $。
(1) 加固后堤坝下底增加的宽度 $ AF $ 为 $ (10\sqrt{3} - 7) \, \text{m} $;
(2) 完成这项工程需要土石 $ (25000\sqrt{3} - 10000) \, \text{m}^3 $。

查看更多完整答案,请扫码查看


