第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
1. 抛物线的相关概念
二次函数 $ y = x ^ { 2 } $ 的图象是一条关于 $ y $ 轴对称、过坐标原点并向上伸展的曲线,像这样的曲线叫做
2. 二次函数 $ y = a x ^ { 2 } ( a \neq 0 ) $ 的图象的性质
二次函数 $ y = a x ^ { 2 } ( a \neq 0 ) $ 的图象是一条
二次函数 $ y = x ^ { 2 } $ 的图象是一条关于 $ y $ 轴对称、过坐标原点并向上伸展的曲线,像这样的曲线叫做
抛物线
。抛物线与它的对称轴的交点叫做抛物线的顶点
。2. 二次函数 $ y = a x ^ { 2 } ( a \neq 0 ) $ 的图象的性质
二次函数 $ y = a x ^ { 2 } ( a \neq 0 ) $ 的图象是一条
抛物线
,它关于y
轴对称,顶点是坐标原点
。当 $ a > 0 $ 时,抛物线的开口向上
,顶点是抛物线的最低
点;当 $ a < 0 $ 时,抛物线的开口向下
,顶点是抛物线的最高
点。
答案:
1. 抛物线 顶点
2. 抛物线 y 坐标原点 上 低 下 高
2. 抛物线 y 坐标原点 上 低 下 高
典例 1
已知一个直角三角形的一条直角边的长为 $ x \mathrm { cm } $,另一条直角边的长是这条直角边的长的 $ 2 $ 倍,则这个直角三角形的面积 $ y ( \mathrm { cm } ^ { 2 } ) $ 与 $ x ( \mathrm { cm } ) $ 之间的函数关系可以用图象大致表示为(
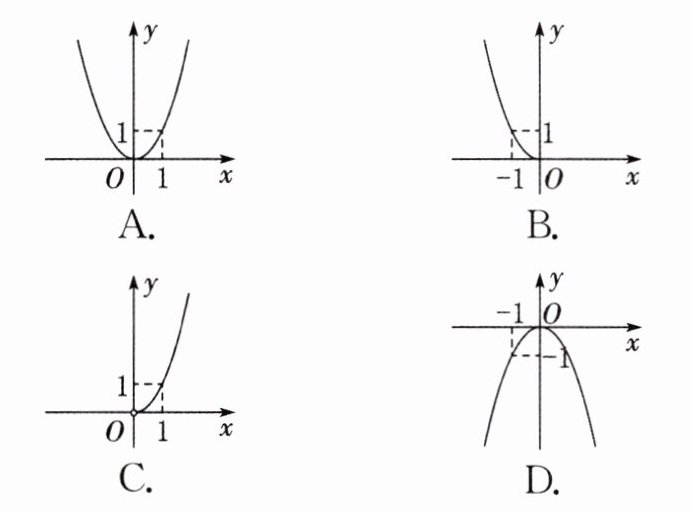
点拨 根据直角三角形的面积的计算公式可确定 $ y $ 与 $ x $ 之间的函数表达式,结合自变量的取值范围可判断相应的函数图象。
解答:
解有所悟:确定实际问题的函数图象时,要先列出函数表达式,相应的图象应该是在对应的自变量的取值范围内的部分。
已知一个直角三角形的一条直角边的长为 $ x \mathrm { cm } $,另一条直角边的长是这条直角边的长的 $ 2 $ 倍,则这个直角三角形的面积 $ y ( \mathrm { cm } ^ { 2 } ) $ 与 $ x ( \mathrm { cm } ) $ 之间的函数关系可以用图象大致表示为(
C
)
点拨 根据直角三角形的面积的计算公式可确定 $ y $ 与 $ x $ 之间的函数表达式,结合自变量的取值范围可判断相应的函数图象。
解答:
解有所悟:确定实际问题的函数图象时,要先列出函数表达式,相应的图象应该是在对应的自变量的取值范围内的部分。
答案:
解:由题意,另一条直角边的长为 $2x$ cm。
直角三角形面积 $y = \frac{1}{2} × x × 2x = x^2$。
$\because x > 0$,且当 $x = 1$ 时,$y = 1$,
$\therefore$ 函数图象为开口向上的抛物线在第一象限的部分,且过点 $(1,1)$。
选项 C 符合题意。
答案:C
直角三角形面积 $y = \frac{1}{2} × x × 2x = x^2$。
$\because x > 0$,且当 $x = 1$ 时,$y = 1$,
$\therefore$ 函数图象为开口向上的抛物线在第一象限的部分,且过点 $(1,1)$。
选项 C 符合题意。
答案:C
典例 2
已知抛物线 $ y = a x ^ { 2 } $ 经过点 $ A ( - 2, - 8 ) $。
(1)求此抛物线对应的函数表达式;
(2)写出这个抛物线的顶点坐标、对称轴、开口方向和位置;
(3)判断点 $ B ( - 1, - 4 ) $ 是否在此抛物线上;
(4)求出此抛物线上纵坐标为 $ - 6 $ 的点的坐标。
点拨 (1)根据抛物线上点的坐标满足其对应的函数表达式,将点 $ A $ 的坐标代入函数表达式得到关于 $ a $ 的方程,然后解方程即可。(2)根据函数图象和性质直接写出顶点坐标、对称轴、开口方向及图象所处的位置即可。(3)把点 $ B $ 的横坐标代入函数表达式,即可判断。(4)把 $ y = - 6 $ 代入函数表达式,即可求得。
解答:
解有所悟:二次函数的表达式与其图象上的点之间的关系如下:点在函数图象上,则点的横、纵坐标满足二次函数表达式;反之,满足二次函数表达式的点必定在该二次函数的图象上。
已知抛物线 $ y = a x ^ { 2 } $ 经过点 $ A ( - 2, - 8 ) $。
(1)求此抛物线对应的函数表达式;
(2)写出这个抛物线的顶点坐标、对称轴、开口方向和位置;
(3)判断点 $ B ( - 1, - 4 ) $ 是否在此抛物线上;
(4)求出此抛物线上纵坐标为 $ - 6 $ 的点的坐标。
点拨 (1)根据抛物线上点的坐标满足其对应的函数表达式,将点 $ A $ 的坐标代入函数表达式得到关于 $ a $ 的方程,然后解方程即可。(2)根据函数图象和性质直接写出顶点坐标、对称轴、开口方向及图象所处的位置即可。(3)把点 $ B $ 的横坐标代入函数表达式,即可判断。(4)把 $ y = - 6 $ 代入函数表达式,即可求得。
解答:
解有所悟:二次函数的表达式与其图象上的点之间的关系如下:点在函数图象上,则点的横、纵坐标满足二次函数表达式;反之,满足二次函数表达式的点必定在该二次函数的图象上。
答案:
(1)解:
∵抛物线$y=ax^{2}$经过点$A(-2,-8)$
∴$a\cdot(-2)^{2}=-8$
$4a=-8$
解得$a=-2$
∴此抛物线对应的函数表达式为$y=-2x^{2}$
(2)顶点坐标为$(0,0)$,对称轴为$y$轴,开口向下,位于$x$轴下方
(3)解:把$x=-1$代入$y=-2x^{2}$
得$y=-2×(-1)^{2}=-2×1=-2$
∵$-2\neq-4$
∴点$B(-1,-4)$不在此抛物线上
(4)解:把$y=-6$代入$y=-2x^{2}$
得$-6=-2x^{2}$
$x^{2}=3$
解得$x=\pm\sqrt{3}$
∴此抛物线上纵坐标为$-6$的点的坐标为$(\sqrt{3},-6)$或$(-\sqrt{3},-6)$
(1)解:
∵抛物线$y=ax^{2}$经过点$A(-2,-8)$
∴$a\cdot(-2)^{2}=-8$
$4a=-8$
解得$a=-2$
∴此抛物线对应的函数表达式为$y=-2x^{2}$
(2)顶点坐标为$(0,0)$,对称轴为$y$轴,开口向下,位于$x$轴下方
(3)解:把$x=-1$代入$y=-2x^{2}$
得$y=-2×(-1)^{2}=-2×1=-2$
∵$-2\neq-4$
∴点$B(-1,-4)$不在此抛物线上
(4)解:把$y=-6$代入$y=-2x^{2}$
得$-6=-2x^{2}$
$x^{2}=3$
解得$x=\pm\sqrt{3}$
∴此抛物线上纵坐标为$-6$的点的坐标为$(\sqrt{3},-6)$或$(-\sqrt{3},-6)$
查看更多完整答案,请扫码查看


