《2025年暑期升级训练八年级数学浙教版浙江教育出版社》

22. (8 分)如图,在$□ ABCD$中,对角线 AC 与 BD 相交于点 O,点 E,F 在 AC 上,且$OE= OF$,连结 DE 并延长至点 M,使$DE= ME$,连结 MF,DF,BE,BF,BM.
(1)当$DF= MF$时,求证：四边形 EMBF 是矩形.
(2)当$\triangle DMF$满足什么条件时,四边形 EMBF 是正方形？请说明理由.

答案：
(1) 证明：
∵ 四边形 $ABCD$ 是平行四边形，
∴ $OB=OD$。
∵ $OE=OF$，
∴ 四边形 $DEBF$ 是平行四边形。
∴ $DE // FB$，$DE=FB$。
∵ $DE=ME$，
∴ $ME=BF$。
∵ $ME // BF$，
∴ 四边形 $EMBF$ 是平行四边形。
∵ 四边形 $DEBF$ 是平行四边形，
∴ $DF=EB$。
∵ $DF=MF$，
∴ $MF=EB$。
∴ 四边形 $EMBF$ 是矩形。
(2) 当 $\triangle DMF$ 满足 $DF=MF$ 且 $\angle DFM=90^\circ$ 时，四边形 $EMBF$ 是正方形。
理由：
由
(1)知，当 $DF=MF$ 时，四边形 $EMBF$ 是矩形。
在 $\triangle DMF$ 中，$\angle DFM=90^\circ$，$E$ 是斜边 $DM$ 的中点，
∴ $EF=\frac{1}{2}DM=EM$，即 $EF=EM$。
∴ 四边形 $EMBF$ 是正方形。

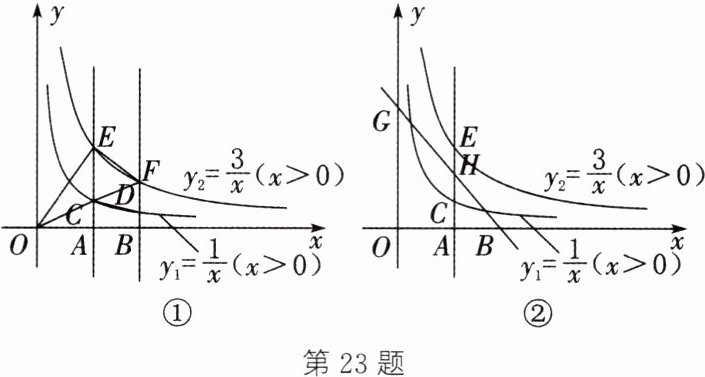
23. (12 分)如图①,在平面直角坐标系中,线段 AB 在 x 轴的正半轴上移动,且$AB= 1$,过点 A,B 作 y 轴的平行线,分别交函数$y_{1}= \frac{1}{x}(x＞0)与y_{2}= \frac{3}{x}(x＞0)$的图象于点 C,E 和点 D,F,设点 A 的横坐标为$m(m＞0)$.
(1)连结 OC,OE,求$\triangle OCE$的面积.
(2)连结 CF,当 m 为何值时,四边形 ABFC 是矩形？
(3)连结 CD,EF,试判断四边形 CDFE 能否是平行四边形,并说明理由.
(4)如图②,经过点 B 和 y 轴上的点$G(0,4)$作直线 BG,交直线 AC 于点 H. 若点 H 的纵坐标为正整数,请求出整数 m 的值.

答案：
(1)
∵点A的横坐标为m，且AC//y轴，
∴点C的坐标为$(m,\frac{1}{m})$，点E的坐标为$(m,\frac{3}{m})$．
∴$CE=\frac{3}{m}-\frac{1}{m}=\frac{2}{m}$．
∴$S_{\triangle OCE}=\frac{1}{2}\cdot CE\cdot OA=\frac{1}{2}\cdot \frac{2}{m}\cdot m=1$．
(2)
∵四边形ABFC是矩形，
∴$AC=BF$．
∵$AB=1$，点A的横坐标为m，
∴点B的横坐标为$m+1$．
∴点C的坐标为$(m,\frac{1}{m})$，点F的坐标为$(m+1,\frac{3}{m+1})$．
∴$AC=\frac{1}{m}$，$BF=\frac{3}{m+1}$．
∴$\frac{1}{m}=\frac{3}{m+1}$，解得$m=\frac{1}{2}$．
经检验，$m=\frac{1}{2}$是原分式方程的解，且符合题意．
∴$m=\frac{1}{2}$．
(3) 不能．理由：
点C的坐标为$(m,\frac{1}{m})$，点E的坐标为$(m,\frac{3}{m})$，
点D的坐标为$(m+1,\frac{1}{m+1})$，点F的坐标为$(m+1,\frac{3}{m+1})$．
∴$CE=\frac{3}{m}-\frac{1}{m}=\frac{2}{m}$，$DF=\frac{3}{m+1}-\frac{1}{m+1}=\frac{2}{m+1}$．
∵$\frac{2}{m}\neq\frac{2}{m+1}$，
∴$CE\neq DF$．
∴四边形CDFE不能是平行四边形．
(4) 设直线BG的函数表达式为$y=kx+4(k\neq0)$．
将$B(m+1,0)$代入，得$k(m+1)+4=0$，解得$k=-\frac{4}{m+1}$．
∴直线BG的表达式为$y=-\frac{4}{m+1}x+4$．
将$x=m$代入，得$y=-\frac{4m}{m+1}+4=\frac{4}{m+1}$，
∴点H的坐标为$(m,\frac{4}{m+1})$．
∵点H的纵坐标为正整数，m为整数，且$m＞0$，
∴$m+1=2$或$m+1=4$，解得$m=1$或$3$．
∴整数m的值为1或3．