《2025年暑期升级训练八年级数学浙教版浙江教育出版社》

运用二次函数求实际问题中的最大值或最小值,首先应当求出函数表达式和自变量的取值范围,然后通过配方变形,或利用公式求它的最大值或最小值. 值得注意的是,由此求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内.

答案： 自变量的取值范围；配方变形；公式；取值范围内

典例1
已知二次函数 $ y = x ^ { 2 } - 4 x + 2 $,当 $ - 1 \leq x \leq 3 $ 时,下列说法中,正确的是(D)
A.有最大值 $ - 1 $,有最小值 $ - 2 $
B.有最大值 $ 0 $,有最小值 $ - 1 $
C.有最大值 $ 7 $,有最小值 $ - 1 $
D.有最大值 $ 7 $,有最小值 $ - 2 $
点拨 先运用配方法将函数表达式整理成顶点式的形式,从而确定抛物线的对称轴和顶点坐标,再结合给定的 $ x $ 的取值范围以及二次函数的性质判断.
解答：
解有所悟：解决确定给定的自变量的取值范围的二次函数最值问题时,若对称轴在给出的取值范围内,则要判断顶点是相应函数图象的最高点还是最低点,再结合给定范围的两端点相对应的函数值的大小进行判断.

答案： D 解析：
∵ $ y = x ^ { 2 } - 4 x + 2 = ( x - 2 ) ^ { 2 } - 2 $，
∴ 其图象的顶点坐标为 $ ( 2 , - 2 ) $，当 $ x ＞ 2 $ 时，$ y $ 随 $ x $ 的增大而增大。
∵ $ x ＜ 2 $ 时，$ y $ 随 $ x $ 的增大而减小。
∵ $ - 1 \leqslant x \leqslant 3 $，
∴ 当 $ x = 2 $ 时，函数有最小值 $ - 2 $。
∵ 当 $ x = - 1 $ 时，$ y = 9 - 2 = 7 $；当 $ x = 3 $ 时，$ y = 1 - 2 = - 1 $，且 $ 7 ＞ - 1 $，
∴ 当 $ x = - 1 $ 时，函数有最大值 $ 7 $。

典例2
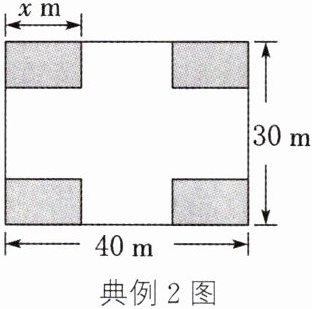
某小区业主委员会决定把一块长为 $ 40 \mathrm { m } $、宽为 $ 30 \mathrm { m } $ 的矩形空地建成健身广场,设计方案如图所示,涂色区域为绿化区(四块绿化区为全等的矩形),空白区域为活动区,且四周的 $ 4 $ 个出口的宽度相同,其宽度不小于 $ 14 \mathrm { m } $,不大于 $ 26 \mathrm { m } $. 设绿化区的较长边为 $ x \mathrm { m } $,活动区的面积为 $ y \mathrm { m } ^ { 2 } $.
(1) ① 出口的宽度为$40 - 2x$ $ \mathrm { m } $(用含 $ x $ 的式子表示)；
② 求 $ x $ 的取值范围.
(2) 求活动区的最大面积.

点拨 (1) ① 根据图形可得出出口的宽度. ② 根据“出口的宽度不小于 $ 14 \mathrm { m } $,不大于 $ 26 \mathrm { m } $”列不等式组,可求得 $ x $ 的取值范围. (2) 先根据“活动区的面积 $ = $ 矩形的面积 $ - $ 四块绿化区的面积”列出函数表达式,再根据二次函数的增减性可求得函数的最大值.
解答：
（1）② 由出口宽度不小于$14\mathrm{m}$，不大于$26\mathrm{m}$，得：
$14 \leqslant 40 - 2x \leqslant 26$
$-26 \leqslant 2x - 40 \leqslant -14$
$14 \leqslant 2x \leqslant 26$
$7 \leqslant x \leqslant 13$
$\therefore x$的取值范围是$7 \leqslant x \leqslant 13$
（2）绿化区短边为：$\frac{30 - (40 - 2x)}{2} = x - 5$
活动区面积$y = 40×30 - 4x(x - 5)$
$= 1200 - 4x^2 + 20x$
$= -4x^2 + 20x + 1200$
$= -4\left(x - \frac{5}{2}\right)^2 + 1225$
$\because a = -4 ＜ 0$，对称轴$x = \frac{5}{2}$
当$7 \leqslant x \leqslant 13$时，$y$随$x$增大而减小
$\therefore$当$x = 7$时，$y_{\text{max}} = -4×7^2 + 20×7 + 1200 = 1144$
答：活动区的最大面积为$1144\mathrm{m}^2$
解有所悟：解这类与几何图形的面积有关的最值问题时,首先需要借助几何图形,建立变量之间的二次函数关系,再结合题意判断自变量的取值范围. 若顶点的横坐标在上述范围内,则函数的最值为顶点的纵坐标；若顶点的横坐标不在上述范围内,则需要根据函数的增减性,借助函数图象来寻找最高(或最低)点,此点的纵坐标才是函数的最值.

答案： （1）① $40 - 2x$
② 由出口宽度不小于$14\mathrm{m}$，不大于$26\mathrm{m}$，得：
$14 \leqslant 40 - 2x \leqslant 26$
$-26 \leqslant 2x - 40 \leqslant -14$
$14 \leqslant 2x \leqslant 26$
$7 \leqslant x \leqslant 13$
$\therefore x$的取值范围是$7 \leqslant x \leqslant 13$
（2）绿化区短边为：$\frac{30 - (40 - 2x)}{2} = x - 5$
活动区面积$y = 40×30 - 4x(x - 5)$
$= 1200 - 4x^2 + 20x$
$= -4x^2 + 20x + 1200$
$= -4\left(x - \frac{5}{2}\right)^2 + 1225$
$\because a = -4 ＜ 0$，对称轴$x = \frac{5}{2}$
当$7 \leqslant x \leqslant 13$时，$y$随$x$增大而减小
$\therefore$当$x = 7$时，$y_{\text{max}} = -4×7^2 + 20×7 + 1200 = 1144$
答：活动区的最大面积为$1144\mathrm{m}^2$