《2025年暑期升级训练八年级数学浙教版浙江教育出版社》

1. 某服装店将进价为每件100元的服装按每件x(x＞100)元的价格出售,每天可销售(200-x)件.若想要获得最大利润,则x应定为(A)
A.150
B.160
C.170
D.180

答案： 解：设每天的利润为y元。
由题意得：y=(x-100)(200-x)
展开得：y=-x²+300x-20000
配方得：y=-(x-150)²+2500
∵a=-1＜0，抛物线开口向下，
∴当x=150时，y有最大值。
答案：A

2. 甲、乙两船航行于海上,甲船的位置在乙船北方125km处,以15km/h的速度向东行驶,乙船以20km/h的速度向北行驶,则经过4h,两船之间的距离最近,最近距离是75km.

答案： 解：设经过 $ t $ h，两船之间的距离为 $ s $ km。
此时甲船向东行驶的距离为 $ 15t $ km，乙船向北行驶的距离为 $ 20t $ km。
甲船初始位置在乙船北方125km处，所以乙船相对于甲船初始位置的南北方向距离为 $ (125 - 20t) $ km，东西方向距离为 $ 15t $ km。
根据勾股定理，两船距离 $ s = \sqrt{(15t)^2 + (125 - 20t)^2} $。
对 $ s^2 = (15t)^2 + (125 - 20t)^2 $ 化简：$ s^2 = 225t^2 + 15625 - 5000t + 400t^2 = 625t^2 - 5000t + 15625 $。
二次函数 $ s^2 = 625t^2 - 5000t + 15625 $ 的对称轴为 $ t = -\frac{b}{2a} = \frac{5000}{2 × 625} = 4 $。
当 $ t = 4 $ 时，$ s^2 = 625 × 16 - 5000 × 4 + 15625 = 10000 - 20000 + 15625 = 5625 $，则 $ s = 75 $。
经过 $ 4 $ h，两船之间的距离最近，最近距离是 $ 75 $ km。
4；75

3. 行驶中的汽车刹车后,由于惯性的作用,还会继续向前滑行一段距离,这段距离称为刹车距离.某汽车的刹车距离s(km)与车速x(km/h)之间的函数表达式为$s= 0.01x-0.004x^2,$则刹车时该汽车的最大刹车距离为0.00625km.

答案： 解：对于函数$s = -0.004x^2 + 0.01x$，其中$a=-0.004$，$b=0.01$。
因为$a=-0.004\lt0$，所以函数图象开口向下，有最大值。
当$x = -\frac{b}{2a} = -\frac{0.01}{2×(-0.004)} = 1.25$时，$s$取得最大值。
将$x = 1.25$代入函数得：
$s = 0.01×1.25 - 0.004×(1.25)^2$
$= 0.0125 - 0.004×1.5625$
$= 0.0125 - 0.00625$
$= 0.00625$
0.00625

4. 如图,在△ABC中,∠B= 90°,AB= 6cm,BC= 8cm,点P从点A出发沿边AB向点B以1cm/s的速度移动,点Q从点B出发沿边BC向点C以2cm/s的速度移动.如果点P,Q分别从点A,B同时出发,当P,Q两点移动几秒时,PQ的长最小?是多少?

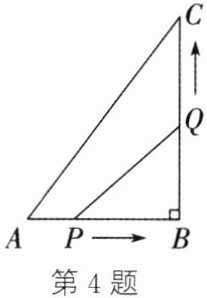
答案： 解：设P，Q两点移动$t\ s$。
由题意，得$PB=(6 - t)\ cm$，$BQ = 2t\ cm$。
在$Rt\triangle PBQ$中，由勾股定理，得$PQ^2 = PB^2 + BQ^2$。
设$PQ^2 = y\ cm^2$，则$y=(6 - t)^2+(2t)^2$，
化简得$y = 5t^2 - 12t + 36 = 5(t - \frac{6}{5})^2 + \frac{144}{5}$。
因为点P从A到B需$6\ s$，点Q从B到C需$\frac{8}{2}=4\ s$，所以$0\leq t\leq4$。
当$t = \frac{6}{5}$时，$y$取得最小值$\frac{144}{5}$，
此时$PQ = \sqrt{\frac{144}{5}} = \frac{12\sqrt{5}}{5}\ cm$。
答：当P，Q两点移动$\frac{6}{5}\ s$时，PQ的长最小，是$\frac{12\sqrt{5}}{5}\ cm$。

5. (宁波中考)为了落实劳动教育,某学校邀请专家指导学生进行小番茄的种植,经过试验,其平均单株的产量y(千克)与每平方米种植的株数x(2≤x≤8,且x为整数)构成一种函数关系.每平方米种植2株时,平均单株的产量为4千克;以同样的栽培条件,每平方米种植的株数每增加1,平均单株的产量减少0.5千克.
(1)求y关于x的函数表达式.
(2)当每平方米种植多少株时,能获得最大的产量?最大产量为多少千克?

答案： （1）解：由题意得，$y = 4 - 0.5(x - 2)$，化简得$y = -0.5x + 5$。所以$y$关于$x$的函数表达式为$y = -0.5x + 5$（$2\leq x\leq8$，且$x$为整数）。
（2）解：设每平方米小番茄的产量为$W$千克，根据题意可得$W = x(-0.5x + 5) = -0.5x^2 + 5x$，配方得$W = -0.5(x - 5)^2 + 12.5$。因为$-0.5\lt0$，$2\leq x\leq8$且$x$为整数，所以当$x = 5$时，$W$取得最大值$12.5$。即当每平方米种植$5$株时，能获得最大产量，最大产量为$12.5$千克。

6. (铜仁中考)为实施“乡村振兴”计划,某村产业合作社种植了“千亩桃园”.2022年桃子丰收,该村产业合作社销售前对本地市场进行调查发现:当批发价为4千元/吨时,每天可售出12吨,每吨涨1千元,每天的销量将减少2吨.据测算,平均每吨的投入成本为2千元.为了抢占市场,薄利多销,该村产业合作社决定,批发价每吨不低于4千元,不高于5.5千元.
(1)请求出每天的销量y(吨)与批发价x(千元/吨)之间的函数表达式,并直接写出自变量x的取值范围.
(2)当批发价定为多少时,每天获得的利润最大?最大利润是多少?

答案： （1）解：根据题意，得
$y = 12 - 2(x - 4) = -2x + 20$
自变量$x$的取值范围为$4 \leq x \leq 5.5$
（2）解：设每天获得的利润为$w$千元。
根据题意，得
$w = (-2x + 20)(x - 2) = -2x^2 + 24x - 40 = -2(x - 6)^2 + 32$
$\because -2 \lt 0$，
$\therefore$ 当$x \lt 6$时，$w$随$x$的增大而增大。
$\because 4 \leq x \leq 5.5$，
$\therefore$ 当$x = 5.5$时，$w$取得最大值，
此时$w = -2(5.5 - 6)^2 + 32 = 31.5$
答：当批发价定为5.5千元/吨时，每天获得的利润最大，最大利润是31.5千元。