第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
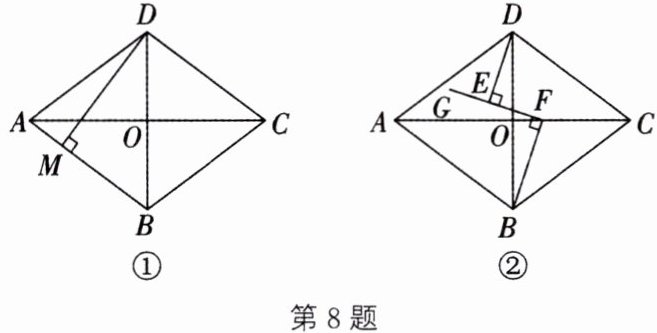
8. 已知四边形$ABCD$是菱形,对角线$AC$,$BD交于点O$。
(1) 如图①,若$AC = 8$,$BD = 6$,$DM\perp AB于点M$,求$DM$的长。
(2) 如图②,$F是AC$上一点,连结$BF$,过点$F作GF\perp BF$,过点$D作DE\perp GF于点E$。若$DE = 4$,$EF = 3$,求$BD$的长。
(1) 如图①,若$AC = 8$,$BD = 6$,$DM\perp AB于点M$,求$DM$的长。
(2) 如图②,$F是AC$上一点,连结$BF$,过点$F作GF\perp BF$,过点$D作DE\perp GF于点E$。若$DE = 4$,$EF = 3$,求$BD$的长。

答案:
$(1) $
∵四边形$ABCD$是菱形,$AC=8,$$BD=6,$$ $
∴$OA=OC=4,$$OD=OB=3,$$AC⊥BD,$$∠AOB=90°。$$ $
∴$AB=\sqrt {(OA²+OB²)}=5。$$ $
∵$S$菱形$ABCD=\frac{1}{2}·AC·BD=AB·DM,$$ $
∴$\frac {1}{2}×8×6=5DM,$解得$DM=\frac {24}{5}。$$ $
$(2) $过点$B$作$BH⊥DE$交$DE$延长线于$H,$连结$DF。$$ $
∵$GF⊥BF,$$DE⊥GF,$$BH⊥DE,$$ $
∴四边形$EFBH$是矩形。$ $
∴$EH=BF,$$BH=EF=3。$$ $
在$Rt△EDF$中,$DF=\sqrt {(DE²+EF²)}=5。$$ $
由菱形对称性得$BF=DF=5,$
∴$EH=5。$$ $
∴$DH=DE+EH=4+5=9。$$ $
在$Rt△BDH$中,$BD=\sqrt {(DH²+BH²)}=3\sqrt {10}$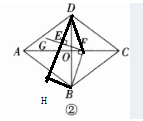
$(1) $
∵四边形$ABCD$是菱形,$AC=8,$$BD=6,$$ $
∴$OA=OC=4,$$OD=OB=3,$$AC⊥BD,$$∠AOB=90°。$$ $
∴$AB=\sqrt {(OA²+OB²)}=5。$$ $
∵$S$菱形$ABCD=\frac{1}{2}·AC·BD=AB·DM,$$ $
∴$\frac {1}{2}×8×6=5DM,$解得$DM=\frac {24}{5}。$$ $
$(2) $过点$B$作$BH⊥DE$交$DE$延长线于$H,$连结$DF。$$ $
∵$GF⊥BF,$$DE⊥GF,$$BH⊥DE,$$ $
∴四边形$EFBH$是矩形。$ $
∴$EH=BF,$$BH=EF=3。$$ $
在$Rt△EDF$中,$DF=\sqrt {(DE²+EF²)}=5。$$ $
由菱形对称性得$BF=DF=5,$
∴$EH=5。$$ $
∴$DH=DE+EH=4+5=9。$$ $
在$Rt△BDH$中,$BD=\sqrt {(DH²+BH²)}=3\sqrt {10}$

9. 如图,在$\triangle ABC$中,延长$BC至点D$,使得$CD = \frac{1}{2}BC$,过$AC的中点E$,作$EF// CD$(点$F在点E$的右侧),且$EF = BC$,连结$DF$。若$AB = 4$,则$DF$的长为(
A.$3$
B.$2$
C.$2\sqrt{2}$
D.$\sqrt{3}$
B
)A.$3$
B.$2$
C.$2\sqrt{2}$
D.$\sqrt{3}$
答案:
1. 首先,取$BC$的中点$G$,连接$EG$:
因为$E$是$AC$的中点,$G$是$BC$的中点,根据三角形中位线定理:三角形的中位线平行于第三边且等于第三边的一半。所以$EG// AB$,且$EG=\frac{1}{2}AB$。
已知$AB = 4$,则$EG=\frac{1}{2}×4 = 2$。
2. 然后,分析线段关系:
因为$CD=\frac{1}{2}BC$,$G$是$BC$中点,所以$CD = BG=GC$。
又因为$EF = BC$,所以$EF=2CD$,即$CD = \frac{1}{2}EF$。
由于$EF// CD$,$EG// AB$,$AB$与$BC$相交,$EG$与$EF$相交,$BG = CD$,$EG// AB$,$EF// CD$,可得$EG// DF$且$EG = DF$(一组对边平行且相等的四边形是平行四边形,这里可通过证明$\triangle EGC\cong\triangle FDC$($SAS$:$EG// AB$,$\angle ECG=\angle FDC$(同位角),$EC = EC$($E$是$AC$中点),$GC = CD$),进而得到$EG = DF$)。
所以$DF = EG=2$,答案是B。
因为$E$是$AC$的中点,$G$是$BC$的中点,根据三角形中位线定理:三角形的中位线平行于第三边且等于第三边的一半。所以$EG// AB$,且$EG=\frac{1}{2}AB$。
已知$AB = 4$,则$EG=\frac{1}{2}×4 = 2$。
2. 然后,分析线段关系:
因为$CD=\frac{1}{2}BC$,$G$是$BC$中点,所以$CD = BG=GC$。
又因为$EF = BC$,所以$EF=2CD$,即$CD = \frac{1}{2}EF$。
由于$EF// CD$,$EG// AB$,$AB$与$BC$相交,$EG$与$EF$相交,$BG = CD$,$EG// AB$,$EF// CD$,可得$EG// DF$且$EG = DF$(一组对边平行且相等的四边形是平行四边形,这里可通过证明$\triangle EGC\cong\triangle FDC$($SAS$:$EG// AB$,$\angle ECG=\angle FDC$(同位角),$EC = EC$($E$是$AC$中点),$GC = CD$),进而得到$EG = DF$)。
所以$DF = EG=2$,答案是B。
10. 如图,在四边形$ABCD$中,$AD与BC$不平行,$F为CD$的中点,$E为AB$的中点,则(
A.$AD + BC < 2EF$
B.$AD + BC > 2EF$
C.$AD + BC = 2EF$
D.无法确定$AD + BC与2EF$的大小关系
B
)A.$AD + BC < 2EF$
B.$AD + BC > 2EF$
C.$AD + BC = 2EF$
D.无法确定$AD + BC与2EF$的大小关系
答案:
1. 首先,连接$BD$,取$BD$的中点$G$:
因为$E$是$AB$的中点,$G$是$BD$的中点,根据三角形中位线定理:三角形的中位线平行于第三边且等于第三边的一半。
在$\triangle ABD$中,$EG$是中位线,所以$EG=\frac{1}{2}AD$。
又因为$F$是$CD$的中点,$G$是$BD$的中点,在$\triangle BCD$中,$FG$是中位线,所以$FG = \frac{1}{2}BC$。
2. 然后,根据三角形三边关系:
在$\triangle EFG$中,根据三角形三边关系$EG + FG>EF$(三角形任意两边之和大于第三边)。
把$EG=\frac{1}{2}AD$,$FG=\frac{1}{2}BC$代入$EG + FG>EF$中,得到$\frac{1}{2}AD+\frac{1}{2}BC>EF$。
不等式两边同时乘以$2$,则$AD + BC>2EF$。
所以$AD + BC>2EF$,答案是B。
因为$E$是$AB$的中点,$G$是$BD$的中点,根据三角形中位线定理:三角形的中位线平行于第三边且等于第三边的一半。
在$\triangle ABD$中,$EG$是中位线,所以$EG=\frac{1}{2}AD$。
又因为$F$是$CD$的中点,$G$是$BD$的中点,在$\triangle BCD$中,$FG$是中位线,所以$FG = \frac{1}{2}BC$。
2. 然后,根据三角形三边关系:
在$\triangle EFG$中,根据三角形三边关系$EG + FG>EF$(三角形任意两边之和大于第三边)。
把$EG=\frac{1}{2}AD$,$FG=\frac{1}{2}BC$代入$EG + FG>EF$中,得到$\frac{1}{2}AD+\frac{1}{2}BC>EF$。
不等式两边同时乘以$2$,则$AD + BC>2EF$。
所以$AD + BC>2EF$,答案是B。
11. 如图,$BD$,$AC是四边形ABCD$的对角线,$E$,$F$,$G$,$H分别是线段AD$,$DB$,$BC$,$AC$的中点。
(1) 求证:线段$EG$,$FH$互相平分。
(2) 当四边形$ABCD$满足什么条件时,$EG\perp FH$?请说明理由。

(1) 求证:线段$EG$,$FH$互相平分。
(2) 当四边形$ABCD$满足什么条件时,$EG\perp FH$?请说明理由。

答案:
1. (1)证明:
连接$EF$,$FG$,$GH$,$HE$。
因为$E$,$F$分别是$AD$,$DB$的中点,所以根据三角形中位线定理,$EF// AB$,且$EF = \frac{1}{2}AB$。
因为$G$,$H$分别是$BC$,$AC$的中点,所以$GH// AB$,且$GH=\frac{1}{2}AB$。
所以$EF// GH$,$EF = GH$。
所以四边形$EFGH$是平行四边形(一组对边平行且相等的四边形是平行四边形)。
因为平行四边形的对角线互相平分,所以线段$EG$,$FH$互相平分。
2. (2)解:
当$AB = CD$时,$EG\perp FH$。
理由:
因为$E$,$H$分别是$AD$,$AC$的中点,所以$EH=\frac{1}{2}CD$。
由(1)知$EF=\frac{1}{2}AB$。
当$AB = CD$时,$EH = EF$。
又因为四边形$EFGH$是平行四边形,所以平行四边形$EFGH$是菱形(一组邻边相等的平行四边形是菱形)。
因为菱形的对角线互相垂直,所以$EG\perp FH$。
综上,(1)得证;(2)当$AB = CD$时,$EG\perp FH$。
1. (1)证明:
连接$EF$,$FG$,$GH$,$HE$。
因为$E$,$F$分别是$AD$,$DB$的中点,所以根据三角形中位线定理,$EF// AB$,且$EF = \frac{1}{2}AB$。
因为$G$,$H$分别是$BC$,$AC$的中点,所以$GH// AB$,且$GH=\frac{1}{2}AB$。
所以$EF// GH$,$EF = GH$。
所以四边形$EFGH$是平行四边形(一组对边平行且相等的四边形是平行四边形)。
因为平行四边形的对角线互相平分,所以线段$EG$,$FH$互相平分。
2. (2)解:
当$AB = CD$时,$EG\perp FH$。
理由:
因为$E$,$H$分别是$AD$,$AC$的中点,所以$EH=\frac{1}{2}CD$。
由(1)知$EF=\frac{1}{2}AB$。
当$AB = CD$时,$EH = EF$。
又因为四边形$EFGH$是平行四边形,所以平行四边形$EFGH$是菱形(一组邻边相等的平行四边形是菱形)。
因为菱形的对角线互相垂直,所以$EG\perp FH$。
综上,(1)得证;(2)当$AB = CD$时,$EG\perp FH$。

查看更多完整答案,请扫码查看


