《2025年暑期升级训练八年级数学浙教版浙江教育出版社》

12. * 如图, 点 $ A $ 在反比例函数 $ y = -\frac{8}{x}(x ＜ 0) $ 的图象上, 点 $ B $ 在第一象限, $ OB \perp OA $, 且 $ OB = OA $.
(1) 若反比例函数 $ y = \frac{k}{x}(x ＞ 0) $ 的图象经过点 $ B $, 求 $ k $ 的值;
(2) 若点 $ A $ 的横坐标为 $ -4 $, 点 $ P $ 在第一象限, 且在直线 $ AB $ 上 (不与点 $ B $ 重合), $ S_{\triangle POB} = S_{\triangle AOB} $, 求点 $ P $ 的坐标.

答案：

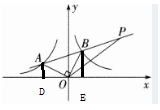
(1)过点A作AD⊥x轴于点D，过点B作BE⊥x轴于点E，则∠ADO=∠OEB=90°。
∵点A在反比例函数$y = -\frac{8}{x}(x ＜ 0)$的图象上，
∴$S_{\triangle AOD} = \frac{1}{2} × |-8| = 4$。
∵OB⊥OA，
∴∠AOB=90°，
∴∠AOD+∠BOE=90°。
∵∠OEB=90°，
∴∠BOE+∠OBE=90°，
∴∠AOD=∠OBE。
在△AOD和△OBE中，
$\begin{cases} \angle AOD = \angle OBE \\\angle ADO = \angle OEB \\OA = BO \end{cases}$，
∴△AOD≌△OBE(AAS)，
∴$S_{\triangle AOD} = S_{\triangle OBE} = 4$。
∵点B在反比例函数$y = \frac{k}{x}(x ＞ 0)$的图象上，
∴$S_{\triangle OBE} = \frac{1}{2}|k| = 4$，
∴|k|=8。
∵点B在第一象限，
∴k＞0，
∴k=8。
(2)
∵点A的横坐标为-4，代入$y = -\frac{8}{x}$得$y = 2$，
∴A(-4,2)。
∴AD=2，OD=4。
∵△AOD≌△OBE，
∴OE=AD=2，BE=OD=4，
∴B(2,4)。
设直线AB的解析式为$y = mx + n$，将A(-4,2)，B(2,4)代入得：
$\begin{cases} -4m + n = 2 \\ 2m + n = 4 \end{cases}$，解得$\begin{cases} m = \frac{1}{3} \\ n = \frac{10}{3} \end{cases}$，
∴直线AB的解析式为$y = \frac{1}{3}x + \frac{10}{3}$。
∵$S_{\triangle POB} = S_{\triangle AOB}$，点P在直线AB上且不与B重合，
∴点P到OB的距离等于点A到OB的距离，即AB=PB（P在B右侧）。
∵A(-4,2)，B(2,4)，
∴向量$\overrightarrow{AB} = (6,2)$，
∴$\overrightarrow{BP} = \overrightarrow{AB} = (6,2)$，
∴P(2+6,4+2)=(8,6)。
∴点P的坐标为(8,6)。

13. (龙东地区中考) 如图, 在平面直角坐标系中, $ O $ 为坐标原点, $ □ OBAD $ 的顶点 $ B $ 在反比例函数 $ y = \frac{3}{x}(x ＞ 0) $ 的图象上, 顶点 $ A $ 在反比例函数 $ y = \frac{k}{x}(x ＜ 0) $ 的图象上, 顶点 $ D $ 在 $ x $ 轴的负半轴上. 若 $ □ OBAD $ 的面积是 5, 则 $ k $ 的值是 ( D )
A.2
B.1
C.-1
D.-2

答案： 解：设点$ B $的坐标为$ (m,\frac{3}{m}) $（$ m＞0 $），点$ A $的坐标为$ (n,\frac{k}{n}) $（$ n＜0 $）。
因为四边形$ OBAD $是平行四边形，所以$ AD // OB $且$ AD = OB $，$ OD $在$ x $轴负半轴上，点$ D $坐标为$ (d,0) $（$ d＜0 $）。
由平行四边形对边相等且平行可得：$ A $点纵坐标与$ B $点纵坐标相等，即$ \frac{k}{n}=\frac{3}{m} $，$ OB $的长度在水平方向的投影为$ m $，$ AD $的长度在水平方向的投影为$ n - d $，所以$ m = n - d $。
平行四边形$ OBAD $的面积为底$ OD $的长度乘以高（$ B $点纵坐标），$ OD = -d $，高为$ \frac{3}{m} $，则面积$ S = (-d) × \frac{3}{m} = 5 $。
又因为$ d = n - m $，所以$ - (n - m) × \frac{3}{m} = 5 $，即$ (m - n) × \frac{3}{m} = 5 $，$ 3 - \frac{3n}{m} = 5 $，$ -\frac{3n}{m} = 2 $，$ \frac{n}{m} = -\frac{2}{3} $。
由$ \frac{k}{n}=\frac{3}{m} $可得$ k = \frac{3n}{m} = 3 × (-\frac{2}{3}) = -2 $。
综上，$ k = -2 $。
答案：D

14. (十堰中考) 如图, 正方形 $ ABCD $ 的顶点分别在反比例函数 $ y = \frac{k_1}{x}(x ＞ 0) $ 和 $ y = \frac{k_2}{x}(x ＞ 0) $ 的图象上. 若 $ BD // y $ 轴, 点 $ D $ 的横坐标为 3, 则 $ k_1 + k_2 $ 的值为 ( )

A.36
B.18
C.12
D.9

答案：
B解析:如图,连结AC,交BD于点E.
∵四边形ABCD是正方形，
∴AE=BE=CE=DE.设AE=BE=CE=DE=m,D(3,a).
∵BD//y轴,
∴B(3,a + 2m),A(3 + m,a + m).
∵点A,B都在反比例函数y=$\frac{k_{1}}{x}$(x＞0)的图象上，
∴(3 + m)(a + m)=3(a + 2m).
∵m≠0,
∴m=3−a.
∴B(3,6−a).
∵点B(3,6−a)在反比例函数y=$\frac{k_{1}}{x}$(x＞0)的图象上,点D(3,a)在反比例函数y=$\frac{k_{2}}{x}$(x＞0)的图象上，
∴k₁=3(6−a)=18−3a,k₂=3a.
∴k₁ + k₂=18−3a+3a=18.

15. 如图, 在平面直角坐标系中, 矩形 $ OABC $ 的两边分别在 $ x $ 轴、 $ y $ 轴的正半轴上, $ OA = 6 $, $ OC = 2\sqrt{3} $, 点 $ E $, $ F $ 分别在边 $ OA $, $ CB $ 上, 且四边形 $ OFBE $ 是菱形.
(1) 求菱形 $ OFBE $ 的边长;
(2) 若反比例函数 $ y = \frac{k}{x}(x ＞ 0) $ 的图象过点 $ F $, 交边 $ AB $ 于点 $ D $, 连结 $ DF $, 求 $ \triangle BDF $ 的面积.

答案： 1. （1）
解：因为四边形$OABC$是矩形，$OA = 6$，$OC = 2\sqrt{3}$，四边形$OFBE$是菱形。
设$OE=OF = FB = BE=x$，则$AE=OA - OE=6 - x$。
在$Rt\triangle ABE$中，$AB = OC = 2\sqrt{3}$，根据勾股定理$BE^{2}=AB^{2}+AE^{2}$。
即$x^{2}=(2\sqrt{3})^{2}+(6 - x)^{2}$。
展开得$x^{2}=12 + 36-12x+x^{2}$。
移项可得$x^{2}-x^{2}+12x=12 + 36$。
合并同类项得$12x = 48$，解得$x = 4$。
所以菱形$OFBE$的边长为$4$。
2. （2）
解：因为$OF = 4$，$OC = 2\sqrt{3}$，在$Rt\triangle OCF$中，根据勾股定理$CF=\sqrt{OF^{2}-OC^{2}}$。
把$OF = 4$，$OC = 2\sqrt{3}$代入得$CF=\sqrt{16 - 12}=\sqrt{4}=2$。
所以$F$点坐标为$(2,2\sqrt{3})$。
因为反比例函数$y=\frac{k}{x}(x\gt0)$的图象过点$F(2,2\sqrt{3})$，把$x = 2$，$y = 2\sqrt{3}$代入$y=\frac{k}{x}$得$k=xy=2×2\sqrt{3}=4\sqrt{3}$，则反比例函数解析式为$y=\frac{4\sqrt{3}}{x}$。
因为$AB$边所在直线$x = 6$，把$x = 6$代入$y=\frac{4\sqrt{3}}{x}$得$y=\frac{4\sqrt{3}}{6}=\frac{2\sqrt{3}}{3}$，所以$D$点坐标为$(6,\frac{2\sqrt{3}}{3})$。
又因为$B$点坐标为$(6,2\sqrt{3})$，$FB = 4$。
根据三角形面积公式$S_{\triangle BDF}=\frac{1}{2}× FB×(2\sqrt{3}-\frac{2\sqrt{3}}{3})$。
先计算$2\sqrt{3}-\frac{2\sqrt{3}}{3}=\frac{6\sqrt{3}-2\sqrt{3}}{3}=\frac{4\sqrt{3}}{3}$。
再计算$S_{\triangle BDF}=\frac{1}{2}×4×\frac{4\sqrt{3}}{3}=\frac{8\sqrt{3}}{3}$。
综上，（1）菱形$OFBE$的边长为$4$；（2）$\triangle BDF$的面积为$\frac{8\sqrt{3}}{3}$。