《2025年暑期升级训练八年级数学浙教版浙江教育出版社》

我们把形如 $ y = $$ax^{2}+bx+c$(其中 $ a , b , c $ 是常数,$ a \neq 0 $)的函数叫做二次函数,称 $ a $ 为二次项系数,$ b $ 为一次项系数,$ c $ 为常数项。

答案： $ax^{2}+bx+c$ 二次项系数 一次项系数 常数项

典例 1 函数 $ y = 3 x ^ { 2 } + ( 2 - 3 x ) ( 2 x + 1 ) $ 是二次函数吗？若是二次函数,请指出二次项系数、一次项系数和常数项。
点拨 先把给出的函数表达式通过去括号、合并同类项等方式进行变形整理,根据整理后的表达式的形式进行判断。
解答：
解有所悟：确定一个函数是否为二次函数,关键是看它经过变形整理后是否符合二次函数的一般形式。

答案： 解：$y = 3x^{2}+(2 - 3x)(2x + 1)$
$=3x^{2}+[2×2x + 2×1 - 3x×2x - 3x×1]$
$=3x^{2}+(4x + 2 - 6x^{2} - 3x)$
$=3x^{2}+(x + 2 - 6x^{2})$
$=3x^{2} - 6x^{2}+x + 2$
$=-3x^{2}+x + 2$
$\therefore$ 该函数是二次函数，二次项系数为$-3$，一次项系数为$1$，常数项为$2$。

典例 2 如图,有长 $ 24 $ 米的篱笆,一边利用墙(墙的最大可用长度为 $ 10 $ 米)围成中间隔有一道篱笆的矩形花圃(篱笆全部用完)。设花圃垂直于墙的一边的长 $ AB $ 为 $ x $ 米,面积为 $ y $ 平方米。

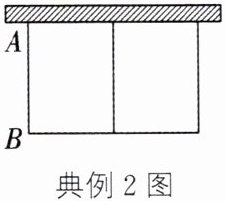
(1)求 $ y $ 与 $ x $ 之间的函数表达式,并写出自变量的取值范围；
(2)根据列出的函数表达式,将下表补充完整。
| $ x $(米) | $ 5 $ | $ 6 $ | $ 7 $ |
| $ y $(平方米) | | | |
点拨(1)由于这个篱笆围成的花圃是矩形,因此,根据矩形的面积等于长乘宽,即可用含 $ x $ 的代数式表示花圃平行于墙的一边的长,从而求得 $ y $ 与 $ x $ 之间的函数表达式,再根据实际问题的意义确定其中自变量 $ x $ 的取值范围。(2)根据列出的函数表达式,已知自变量的值即可求得相应的函数值。
解答：
解有所悟：解答这类关于确定 $ y $ 与 $ x $ 之间的函数表达式的问题的关键是找出问题中隐含的等量关系,再用含 $ x , y $ 的代数式分别表示其中的量,特别要注意其中自变量的取值范围的确定。

答案：
（1）解：
∵花圃垂直于墙的一边的长$AB$为$x$米，
∴花圃平行于墙的一边的长为$(24 - 3x)$米。
∴$y = x(24 - 3x) = -3x^2 + 24x$。
∵墙的最大可用长度为10米，
∴$0 ＜ 24 - 3x \leq 10$，
解得$\frac{14}{3} \leq x ＜ 8$。
∴$y$与$x$之间的函数表达式为$y = -3x^2 + 24x\left(\frac{14}{3} \leq x ＜ 8\right)$。
（2）

典例 3 已知二次函数 $ y = 3 x ^ { 2 } + b x + c $,当 $ x = - 2 $ 时,函数值是 $ 0 $；当 $ x = 1 $ 时,函数值是 $ 6 $。求这个二次函数的表达式。
点拨 将 $ x = - 2 , y = 0 $；$ x = 1 , y = 6 $ 分别代入二次函数的表达式,列出关于 $ b , c $ 的方程组,通过解方程组求得 $ b , c $ 的值,然后将其代入二次函数的表达式即可。
解答：
解有所悟：将给出的自变量和相应的函数值代入函数表达式,即可构建以表达式中未知系数为未知数的方程(组),通过解方程(组)即可确定未知系数的值。

答案： 解：根据题意，将 $ x = -2 $，$ y = 0 $ 和 $ x = 1 $，$ y = 6 $ 分别代入二次函数 $ y = 3x^2 + bx + c $，得
$\begin{cases}3×(-2)^2 + b×(-2) + c = 0 \\3×1^2 + b×1 + c = 6\end{cases}$
化简方程组，得
$\begin{cases}12 - 2b + c = 0 \\3 + b + c = 6\end{cases}$
解得
$\begin{cases}b = 5 \\c = -2\end{cases}$
$\therefore$ 这个二次函数的表达式为 $ y = 3x^2 + 5x - 2 $。