第36页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
4. 如图,在等边三角形$ABC$中,$P为边AB$上的一点,$Q为边AC$上的一点,且$AP = CQ$,$M是线段PQ$的中点,连结$AM$,$PC$。若$AM = 19\mathrm{cm}$,则$PC = $______$\mathrm{cm}$。


答案:
解:延长AM至点N,使MN=AM,连接QN。
∵M是PQ中点,
∴PM=QM。
在△APM和△NQM中,
$\left\{\begin{array}{l} AM=NM\\ ∠AMP=∠NMQ\\ PM=QM\end{array}\right.$
∴△APM≌△NQM(SAS),
∴AP=QN,∠PAM=∠QNM,
∴AP//QN。
∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠ACB=60°。
∵AP=CQ,AP=QN,
∴QN=CQ。
∵AP//QN,
∴∠BAC=∠AQN=60°,
∴∠NQC=180°-∠AQN=120°。
∵∠ACB=60°,
∴∠QCN=180°-∠ACB=120°,
∴∠NQC=∠QCN。
在△NQC和△PCQ中,
$\left\{\begin{array}{l} QN=CQ\\ ∠NQC=∠QCN\\ QC=CQ\end{array}\right.$(此处修正:应为△NQC和△PCQ对应关系错误,正确为△NQC和△PCQ中QC为公共边,条件应为QN=CQ,∠NQC=∠QCP=120°,QC=CQ,故△NQC≌△PCQ(SAS))
∴NC=PC。
∵AN=AM+MN=2AM=38cm,且AN=NC,
∴PC=AN=38cm。
38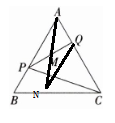
解:延长AM至点N,使MN=AM,连接QN。
∵M是PQ中点,
∴PM=QM。
在△APM和△NQM中,
$\left\{\begin{array}{l} AM=NM\\ ∠AMP=∠NMQ\\ PM=QM\end{array}\right.$
∴△APM≌△NQM(SAS),
∴AP=QN,∠PAM=∠QNM,
∴AP//QN。
∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠ACB=60°。
∵AP=CQ,AP=QN,
∴QN=CQ。
∵AP//QN,
∴∠BAC=∠AQN=60°,
∴∠NQC=180°-∠AQN=120°。
∵∠ACB=60°,
∴∠QCN=180°-∠ACB=120°,
∴∠NQC=∠QCN。
在△NQC和△PCQ中,
$\left\{\begin{array}{l} QN=CQ\\ ∠NQC=∠QCN\\ QC=CQ\end{array}\right.$(此处修正:应为△NQC和△PCQ对应关系错误,正确为△NQC和△PCQ中QC为公共边,条件应为QN=CQ,∠NQC=∠QCP=120°,QC=CQ,故△NQC≌△PCQ(SAS))
∴NC=PC。
∵AN=AM+MN=2AM=38cm,且AN=NC,
∴PC=AN=38cm。
38

5. 如图,分别以$\triangle ABC的边AB$,$AC为边向\triangle ABC外作正方形ABEF和正方形ACNM$,$D是BC$的中点,连结$AD$,$FM$。
(1) 求证:$FM = 2AD$;
(2) 若$AB = 6$,$AC = 8$,$\angle BAC = 60^{\circ}$,求多边形$BCNMFE$的面积。

(1) 求证:$FM = 2AD$;
(2) 若$AB = 6$,$AC = 8$,$\angle BAC = 60^{\circ}$,求多边形$BCNMFE$的面积。

答案:
(1) 证明:延长AD至点K,使DK=AD,连结BK,CK。
∵D是BC的中点,
∴BD=CD。又
∵AD=DK,
∴四边形ABKC是平行四边形。
∴CK=AB,∠BAC+∠KCA=180°。
∵四边形ABEF,ACNM都是正方形,
∴AF=AB,AM=AC,∠BAF=∠CAM=90°。
∴AF=CK,∠BAC+∠FAM=360°-∠BAF-∠CAM=180°。
∴∠FAM=∠KCA。
在△MAF和△ACK中,
$\left\{\begin{array}{l} AF=CK \\ ∠FAM=∠KCA \\ AM=CA \end{array}\right.$
∴△MAF≌△ACK(SAS)。
∴FM=KA。
∵KA=AD+DK=2AD,
∴FM=2AD。
(2) 解:过点B作BH⊥AC于点H。
在Rt△ABH中,∠BAH=60°,
∴∠ABH=30°。
∴AH=$\frac{1}{2}$AB=3。
由勾股定理,得BH=$\sqrt{AB^2-AH^2}=\sqrt{6^2-3^2}=3\sqrt{3}$。
∴S△ABC=$\frac{1}{2}$AC·BH=$\frac{1}{2}×8×3\sqrt{3}=12\sqrt{3}$。
由
(1),△MAF≌△ACK,
∴S△MAF=S△ACK=S△ABC=12$\sqrt{3}$。
多边形BCNMFE的面积=S△ABC+S正方形ABEF+S△MAF+S正方形ACNM
=12$\sqrt{3}$+6×6+12$\sqrt{3}$+8×8=24$\sqrt{3}$+100。
(1) 证明:延长AD至点K,使DK=AD,连结BK,CK。
∵D是BC的中点,
∴BD=CD。又
∵AD=DK,
∴四边形ABKC是平行四边形。
∴CK=AB,∠BAC+∠KCA=180°。
∵四边形ABEF,ACNM都是正方形,
∴AF=AB,AM=AC,∠BAF=∠CAM=90°。
∴AF=CK,∠BAC+∠FAM=360°-∠BAF-∠CAM=180°。
∴∠FAM=∠KCA。
在△MAF和△ACK中,
$\left\{\begin{array}{l} AF=CK \\ ∠FAM=∠KCA \\ AM=CA \end{array}\right.$
∴△MAF≌△ACK(SAS)。
∴FM=KA。
∵KA=AD+DK=2AD,
∴FM=2AD。
(2) 解:过点B作BH⊥AC于点H。
在Rt△ABH中,∠BAH=60°,
∴∠ABH=30°。
∴AH=$\frac{1}{2}$AB=3。
由勾股定理,得BH=$\sqrt{AB^2-AH^2}=\sqrt{6^2-3^2}=3\sqrt{3}$。
∴S△ABC=$\frac{1}{2}$AC·BH=$\frac{1}{2}×8×3\sqrt{3}=12\sqrt{3}$。
由
(1),△MAF≌△ACK,
∴S△MAF=S△ACK=S△ABC=12$\sqrt{3}$。
多边形BCNMFE的面积=S△ABC+S正方形ABEF+S△MAF+S正方形ACNM
=12$\sqrt{3}$+6×6+12$\sqrt{3}$+8×8=24$\sqrt{3}$+100。

6. 如图,$P为矩形ABCD$内一点,且$PA = 4$,$PB = 1$,$PC = 5$,求$PD$的长。


答案:
解:过点P作PE⊥AD于点E,延长EP交BC于点F。
∵四边形ABCD是矩形,
∴∠BAD=∠ADC=∠BCD=∠ABC=90°。
∵PE⊥AD,
∴∠AEF=∠DEF=90°,
∴四边形ABFE和四边形EFCD都是矩形,
∴AE=BF,DE=FC。
由勾股定理得:
AE² + PE² = PA²,
PE² + DE² = PD²,
BF² + PF² = PB²,
FC² + PF² = PC²。
∴PA² + PC² = AE² + PE² + FC² + PF²,
PB² + PD² = BF² + PF² + DE² + PE²。
∵AE=BF,DE=FC,
∴PA² + PC² = PB² + PD²。
∵PA=4,PB=1,PC=5,
∴4² + 5² = 1² + PD²,
即16 + 25 = 1 + PD²,
41 = 1 + PD²,
PD²=40,
PD=2$\sqrt {10}$。
答:PD的长为2$\sqrt {10}$。
解:过点P作PE⊥AD于点E,延长EP交BC于点F。
∵四边形ABCD是矩形,
∴∠BAD=∠ADC=∠BCD=∠ABC=90°。
∵PE⊥AD,
∴∠AEF=∠DEF=90°,
∴四边形ABFE和四边形EFCD都是矩形,
∴AE=BF,DE=FC。
由勾股定理得:
AE² + PE² = PA²,
PE² + DE² = PD²,
BF² + PF² = PB²,
FC² + PF² = PC²。
∴PA² + PC² = AE² + PE² + FC² + PF²,
PB² + PD² = BF² + PF² + DE² + PE²。
∵AE=BF,DE=FC,
∴PA² + PC² = PB² + PD²。
∵PA=4,PB=1,PC=5,
∴4² + 5² = 1² + PD²,
即16 + 25 = 1 + PD²,
41 = 1 + PD²,
PD²=40,
PD=2$\sqrt {10}$。
答:PD的长为2$\sqrt {10}$。
7. 如图,在四边形$ABCD$中,$\angle ABC = \angle ADC = 90^{\circ}$,$AD = CD$。求证:$AB + BC = \sqrt{2}BD$。


答案:
解:过点$D$作$DE\perp AB$交$BA$的延长线于点$E$,作$DF\perp BC$于点$F$。
因为$\angle ABC=\angle ADC = 90^{\circ}$,所以四边形$EBFD$是矩形。
又因为$\angle EAD+\angle DAB = 180^{\circ}$,$\angle DAB+\angle BCD=360^{\circ}-\angle ABC-\angle ADC=180^{\circ}$,所以$\angle EAD=\angle FCD$。
已知$AD = CD$,$\angle AED=\angle CFD = 90^{\circ}$,根据$AAS$(角角边)可得$\triangle ADE\cong\triangle CDF$。
所以$DE=DF$,$AE = CF$。
因为$DE=DF$,四边形$EBFD$是矩形,所以矩形$EBFD$是正方形,则$EB=BF = DF=DE$。
$AB + BC=(EB - AE)+(BF + FC)=EB+BF$。
在正方形$EBFD$中,$BD=\sqrt{2}EB$(正方形对角线与边长关系:设边长为$a$,对角线$l=\sqrt{a^{2}+a^{2}}=\sqrt{2}a$),且$EB + BF = 2EB$(因为$EB=BF$)
所以$AB + BC=\sqrt{2}BD$。
解:过点$D$作$DE\perp AB$交$BA$的延长线于点$E$,作$DF\perp BC$于点$F$。
因为$\angle ABC=\angle ADC = 90^{\circ}$,所以四边形$EBFD$是矩形。
又因为$\angle EAD+\angle DAB = 180^{\circ}$,$\angle DAB+\angle BCD=360^{\circ}-\angle ABC-\angle ADC=180^{\circ}$,所以$\angle EAD=\angle FCD$。
已知$AD = CD$,$\angle AED=\angle CFD = 90^{\circ}$,根据$AAS$(角角边)可得$\triangle ADE\cong\triangle CDF$。
所以$DE=DF$,$AE = CF$。
因为$DE=DF$,四边形$EBFD$是矩形,所以矩形$EBFD$是正方形,则$EB=BF = DF=DE$。
$AB + BC=(EB - AE)+(BF + FC)=EB+BF$。
在正方形$EBFD$中,$BD=\sqrt{2}EB$(正方形对角线与边长关系:设边长为$a$,对角线$l=\sqrt{a^{2}+a^{2}}=\sqrt{2}a$),且$EB + BF = 2EB$(因为$EB=BF$)
所以$AB + BC=\sqrt{2}BD$。
查看更多完整答案,请扫码查看


