第47页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
1. 如图,在$\triangle ABC$中,$AD平分\angle BAC$,$\angle B= 2\angle ADB$,$AB= 3$,$CD= 5$,则$AC$的长为( )

A.15
B.11
C.8
D.6

A.15
B.11
C.8
D.6
答案:
C 解析:如图,在AC上截取AE=AB,连结DE.
∵AD平分∠BAC,
∴∠BAD=∠EAD.在△ABD和△AED中,
∵$\left\{\begin{array}{l} AB=AE,\\ ∠BAD=∠EAD,\\ AD=AD,\end{array}\right.$
∴△ABD≌△AED.
∴∠B=∠AED,BD=ED,∠ADB=∠ADE.
∵∠B=2∠ADB,
∴∠AED=2∠ADB=∠BDE.
∵∠CED=180°−∠AED,∠CDE=180°−∠BDE,
∴∠CED=∠CDE.
∴CD=CE.
∴AC=AE+CE=AB+CD=3+5=8.

C 解析:如图,在AC上截取AE=AB,连结DE.
∵AD平分∠BAC,
∴∠BAD=∠EAD.在△ABD和△AED中,
∵$\left\{\begin{array}{l} AB=AE,\\ ∠BAD=∠EAD,\\ AD=AD,\end{array}\right.$
∴△ABD≌△AED.
∴∠B=∠AED,BD=ED,∠ADB=∠ADE.
∵∠B=2∠ADB,
∴∠AED=2∠ADB=∠BDE.
∵∠CED=180°−∠AED,∠CDE=180°−∠BDE,
∴∠CED=∠CDE.
∴CD=CE.
∴AC=AE+CE=AB+CD=3+5=8.

2. 如图,在$\triangle ABC$中,$AB= AC$,$\angle B= 35^{\circ}$,$D是边BC$上的动点,连结$AD$。若$\triangle ABD$为直角三角形,则$\angle DAC$的度数为(
A.$20^{\circ}$
B.$35^{\circ}$
C.$20^{\circ}或55^{\circ}$
D.$20^{\circ}或35^{\circ}$
C
)A.$20^{\circ}$
B.$35^{\circ}$
C.$20^{\circ}或55^{\circ}$
D.$20^{\circ}或35^{\circ}$
答案:
C 解析:
∵AB=AC,∠B=35°,
∴∠B=∠C=35°.
∴∠BAC=110°.当∠BAD=90°时,∠DAC=110°−90°=20°;当∠ADB=90°,即AD⊥BC时,∠ADC=90°.
∴∠DAC=180°−∠ADC−∠C=55°.综上所述,∠DAC的度数为20°或55°.
∵AB=AC,∠B=35°,
∴∠B=∠C=35°.
∴∠BAC=110°.当∠BAD=90°时,∠DAC=110°−90°=20°;当∠ADB=90°,即AD⊥BC时,∠ADC=90°.
∴∠DAC=180°−∠ADC−∠C=55°.综上所述,∠DAC的度数为20°或55°.
3. 若不等式$\frac{2x+5}{3}-1\leqslant 2-x的解集中x$的每一个值,都能使关于$x的不等式3(x-1)+5>5x+2(m+x)$成立,则$m$的取值范围是(
A.$m>-\frac{3}{5}$
B.$m<-\frac{1}{5}$
C.$m<-\frac{3}{5}$
D.$m>-\frac{1}{5}$
C
)A.$m>-\frac{3}{5}$
B.$m<-\frac{1}{5}$
C.$m<-\frac{3}{5}$
D.$m>-\frac{1}{5}$
答案:
C 解析:解不等式$\frac {2x+5}{3}-1\leq2-x$,得$x\leq\frac {4}{5}$.解不等式$3(x - 1) + 5>5x + 2(m + x)$,得$x<\frac {1 - m}{2}$.
∵不等式$\frac {2x+5}{3}-1\leq2-x$的解集中x的每一个值,都能使关于x的不等式$3(x - 1) + 5>5x + 2(m + x)$成立,
∴$\frac {1 - m}{2}>\frac {4}{5}$,解得$m<-\frac {3}{5}$.
∵不等式$\frac {2x+5}{3}-1\leq2-x$的解集中x的每一个值,都能使关于x的不等式$3(x - 1) + 5>5x + 2(m + x)$成立,
∴$\frac {1 - m}{2}>\frac {4}{5}$,解得$m<-\frac {3}{5}$.
4. 已知$x^{2}+y^{2}+13= 4y-6x$,则化简$\sqrt{6y-4x}$的结果是(
A.0
B.$2\sqrt{6}$
C.$4\sqrt{6}$
D.12
B
)A.0
B.$2\sqrt{6}$
C.$4\sqrt{6}$
D.12
答案:
B 解析:
∵$x^{2}+y^{2}+13 = 4y - 6x$,
∴$x^{2}+6x + 9 + y^{2}-4y + 4 = 0$.
∴$(x + 3)^{2}+(y - 2)^{2}=0$.
∴$x + 3 = 0$,$y - 2 = 0$.
∴$x = - 3$,$y = 2$.
∴$\sqrt {6y - 4x}=\sqrt {6×2 - 4×(-3)}=2\sqrt {6}$.
∵$x^{2}+y^{2}+13 = 4y - 6x$,
∴$x^{2}+6x + 9 + y^{2}-4y + 4 = 0$.
∴$(x + 3)^{2}+(y - 2)^{2}=0$.
∴$x + 3 = 0$,$y - 2 = 0$.
∴$x = - 3$,$y = 2$.
∴$\sqrt {6y - 4x}=\sqrt {6×2 - 4×(-3)}=2\sqrt {6}$.
5. 如图,用四张大小一样的矩形纸片拼成一个正方形$ABCD$,它的面积是75,$AE= 3\sqrt{3}$,图中空白的地方是一个小正方形,那么这个小正方形的周长为(
A.$2\sqrt{3}$
B.$4\sqrt{3}$
C.$5\sqrt{3}$
D.$6\sqrt{3}$
B
)A.$2\sqrt{3}$
B.$4\sqrt{3}$
C.$5\sqrt{3}$
D.$6\sqrt{3}$
答案:
B 解析:由题意,得中间的小正方形的边长为$3\sqrt {3}-(\sqrt {75}-3\sqrt {3})=3\sqrt {3}-(5\sqrt {3}-3\sqrt {3})=\sqrt {3}$.
∴这个小正方形的周长为$4×\sqrt {3}=4\sqrt {3}$.
∴这个小正方形的周长为$4×\sqrt {3}=4\sqrt {3}$.
6. 如图,在四边形$ABCD$中,$\angle A= 90^{\circ}$,$AB= 12$,$AD= 5$,$M$,$N分别为线段BC$,$AB$上的动点,$E$,$F分别为DM$,$MN$的中点,则$EF$的长可能为( )

A.2
B.2.3
C.4
D.7

A.2
B.2.3
C.4
D.7
答案:
C 解析:连结DN.
∵E,F分别为DM,MN的中点,
∴ED=EM,MF=FN,$EF=\frac {1}{2}DN$.
∴当DN的长最大时,EF的长最大,当DN的长最小时,EF的长最小.
∵当点N与点B重合时,DN的长最大,此时$DN = DB=\sqrt {AD^{2}+AB^{2}}=\sqrt {5^{2}+12^{2}}=13$.
∴EF长的最大值为$\frac {1}{2}×13 = 6.5$.
∵∠A = 90°,AD = 5,
∴当点N与点A重合时,DN的长最小,此时DN = AD = 5.
∴EF长的最小值为$\frac {1}{2}×5 = 2.5$.
∴$2.5\leq EF\leq6.5$.
∴EF的长可能为4.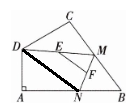
C 解析:连结DN.
∵E,F分别为DM,MN的中点,
∴ED=EM,MF=FN,$EF=\frac {1}{2}DN$.
∴当DN的长最大时,EF的长最大,当DN的长最小时,EF的长最小.
∵当点N与点B重合时,DN的长最大,此时$DN = DB=\sqrt {AD^{2}+AB^{2}}=\sqrt {5^{2}+12^{2}}=13$.
∴EF长的最大值为$\frac {1}{2}×13 = 6.5$.
∵∠A = 90°,AD = 5,
∴当点N与点A重合时,DN的长最小,此时DN = AD = 5.
∴EF长的最小值为$\frac {1}{2}×5 = 2.5$.
∴$2.5\leq EF\leq6.5$.
∴EF的长可能为4.

7. 菱形$ABCD的对角线相交于点O$,$AC= 4$,$BD= 4\sqrt{3}$。将菱形$ABCD$按如图所示的方式折叠,使点$B与点O$重合,折痕为$EF$,则五边形$AEFCD$的周长是(
A.14
B.16
C.$4+4\sqrt{3}$
D.$8+8\sqrt{3}$
A
)A.14
B.16
C.$4+4\sqrt{3}$
D.$8+8\sqrt{3}$
答案:
A 解析:
∵四边形ABCD是菱形,AC = 4,$BD = 4\sqrt {3}$,
∴AB = BC = CD = AD,AC⊥BD,AO = CO = 2,$BO = DO = 2\sqrt {3}$.
∴∠AOB = 90°.
∴在Rt△AOB中,$AB=\sqrt {AO^{2}+BO^{2}} = 4$.
∴AB = BC = CD = AD = 4.由折叠,可知BF = OF,
∴∠FOB = ∠FBO.
∵AC⊥BD,
∴∠BOC = 90°.
∴易得∠FCO = ∠FOC.
∴OF = CF.
∴$OF = CF = BF=\frac {1}{2}BC = 2$.同理,可得$BE = OE = AE=\frac {1}{2}AB = 2$.
∴EF是△ABC的中位线.
∴$EF=\frac {1}{2}AC = 2$.
∴五边形AEFCD的周长 = 4 + 4 + 2 + 2 + 2 = 14.
∵四边形ABCD是菱形,AC = 4,$BD = 4\sqrt {3}$,
∴AB = BC = CD = AD,AC⊥BD,AO = CO = 2,$BO = DO = 2\sqrt {3}$.
∴∠AOB = 90°.
∴在Rt△AOB中,$AB=\sqrt {AO^{2}+BO^{2}} = 4$.
∴AB = BC = CD = AD = 4.由折叠,可知BF = OF,
∴∠FOB = ∠FBO.
∵AC⊥BD,
∴∠BOC = 90°.
∴易得∠FCO = ∠FOC.
∴OF = CF.
∴$OF = CF = BF=\frac {1}{2}BC = 2$.同理,可得$BE = OE = AE=\frac {1}{2}AB = 2$.
∴EF是△ABC的中位线.
∴$EF=\frac {1}{2}AC = 2$.
∴五边形AEFCD的周长 = 4 + 4 + 2 + 2 + 2 = 14.
8. 如图,正方形$ABCD$的边长为12,$BE= EC$,将正方形$ABCD的边DC沿DE折叠到DF$,延长$EF交AB于点G$,连结$DG$,$BF$。有下列结论:①$AG+EC= GE$;②$\triangle BGE$的周长是一个定值;③$\angle GDE= 45^{\circ}$;④若连结$FC$,则$\triangle BFC的面积等于\frac{1}{2}BF\cdot FC$。其中,正确的个数是( )

A.1
B.2
C.3
D.4

A.1
B.2
C.3
D.4
答案:
D 解析:
∵四边形ABCD是正方形,
∴AD = CD,∠A = ∠C = ∠ABC = ∠ADC = 90°.由折叠,可知EC = EF,DF = DC,∠DFE = ∠C = 90°,
∴∠DFG = 90° = ∠A,DF = DA.在Rt△ADG和Rt△FDG中,
∵$\left\{\begin{array}{l} DG = DG,\\ DA = DF,\end{array}\right.$
∴Rt△ADG≌Rt△FDG.
∴AG = FG.
∴AG + EC = FG + EF = GE.故①正确.
∵正方形ABCD的边长是12,
∴AB = BC = 12.
∵BE = EC,
∴BE = EC = EF = 6.设AG = FG = x,则GE = x + 6,BG = 12 - x.在Rt△BGE中,由勾股定理,得$GE^{2}=BE^{2}+BG^{2}$,即$(x + 6)^{2}=6^{2}+(12 - x)^{2}$,解得$x = 4$.
∴AG = FG = 4,BG = 8,GE = 10.
∴△BGE的周长为6 + 8 + 10 = 24,是一个定值.故②正确.
∵Rt△ADG≌Rt△FDG,
∴∠ADG = ∠FDG.由折叠,可得∠CDE = ∠FDE,
∴$∠GDE = ∠FDG+∠FDE=\frac {1}{2}∠ADC = 45^{\circ}$.故③正确.如图,连结FC交DE于点H.根据折叠,可知DE是CF的垂直平分线,
∴FH = CH,∠CHE = 90°.又
∵BE = EC,
∴EH是△CBF的中位线.
∴EH//BF.
∴∠BFC = ∠CHE = 90°.
∴△BFC的面积等于$\frac {1}{2}BF\cdot FC$.故④正确.综上所述,正确的个数是4.

D 解析:
∵四边形ABCD是正方形,
∴AD = CD,∠A = ∠C = ∠ABC = ∠ADC = 90°.由折叠,可知EC = EF,DF = DC,∠DFE = ∠C = 90°,
∴∠DFG = 90° = ∠A,DF = DA.在Rt△ADG和Rt△FDG中,
∵$\left\{\begin{array}{l} DG = DG,\\ DA = DF,\end{array}\right.$
∴Rt△ADG≌Rt△FDG.
∴AG = FG.
∴AG + EC = FG + EF = GE.故①正确.
∵正方形ABCD的边长是12,
∴AB = BC = 12.
∵BE = EC,
∴BE = EC = EF = 6.设AG = FG = x,则GE = x + 6,BG = 12 - x.在Rt△BGE中,由勾股定理,得$GE^{2}=BE^{2}+BG^{2}$,即$(x + 6)^{2}=6^{2}+(12 - x)^{2}$,解得$x = 4$.
∴AG = FG = 4,BG = 8,GE = 10.
∴△BGE的周长为6 + 8 + 10 = 24,是一个定值.故②正确.
∵Rt△ADG≌Rt△FDG,
∴∠ADG = ∠FDG.由折叠,可得∠CDE = ∠FDE,
∴$∠GDE = ∠FDG+∠FDE=\frac {1}{2}∠ADC = 45^{\circ}$.故③正确.如图,连结FC交DE于点H.根据折叠,可知DE是CF的垂直平分线,
∴FH = CH,∠CHE = 90°.又
∵BE = EC,
∴EH是△CBF的中位线.
∴EH//BF.
∴∠BFC = ∠CHE = 90°.
∴△BFC的面积等于$\frac {1}{2}BF\cdot FC$.故④正确.综上所述,正确的个数是4.

查看更多完整答案,请扫码查看


