第3页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
22. (10分)某轮滑特色学校准备修建一个训练轮滑技巧的场地,其侧面示意图如图所示,其横截面为梯形,高1米,AD的长为2米,坡道AB的坡比为$1:1.5$,DC的坡比为$1:2.$
(1)求从点C滑到点B的总长度;
(2)由于场地限制,起跑线到墙的距离为7米,为了安全,起跑线到点C以及点B到墙均需留出1米的距离,通过计算判断该场地是否符合安全要求.

(1)求从点C滑到点B的总长度;
(2)由于场地限制,起跑线到墙的距离为7米,为了安全,起跑线到点C以及点B到墙均需留出1米的距离,通过计算判断该场地是否符合安全要求.

答案:
1. (1)
过点$A$作$AE\perp BC$于点$E$,过点$D$作$DF\perp BC$于点$F$。
因为$AD// BC$,$AE\perp BC$,$DF\perp BC$,所以四边形$AEFD$是矩形,则$EF = AD = 2$米,$AE=DF = 1$米。
已知坡道$AB$的坡比为$1:1.5$,即$\frac{AE}{BE}=\frac{1}{1.5}$,因为$AE = 1$米,所以$BE=1.5$米。
已知$DC$的坡比为$1:2$,即$\frac{DF}{CF}=\frac{1}{2}$,因为$DF = 1$米,所以$CF = 2$米。
那么$BC=BE + EF+CF=1.5 + 2+2=5.5$米。
根据勾股定理,$AB=\sqrt{AE^{2}+BE^{2}}=\sqrt{1^{2}+1.5^{2}}=\sqrt{1 + 2.25}=\sqrt{3.25}=\frac{\sqrt{13}}{2}$米,$CD=\sqrt{DF^{2}+CF^{2}}=\sqrt{1^{2}+2^{2}}=\sqrt{1 + 4}=\sqrt{5}$米。
从点$C$滑到点$B$的总长度为$BC + AB+CD=5.5+\frac{\sqrt{13}}{2}+\sqrt{5}\approx5.5 + 1.80+2.24 = 9.54$米。
2. (2)
解:由(1)可知$BC = 5.5$米。
起跑线到墙的距离为$7$米,起跑线到点$C$以及点$B$到墙均需留出$1$米的距离,那么$BC + 1+1=5.5 + 2=7.5$米。
因为$7.5\gt7$,所以该场地不符合安全要求。
综上,(1)从点$C$滑到点$B$的总长度约为$9.54$米;(2)该场地不符合安全要求。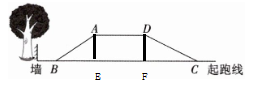
1. (1)
过点$A$作$AE\perp BC$于点$E$,过点$D$作$DF\perp BC$于点$F$。
因为$AD// BC$,$AE\perp BC$,$DF\perp BC$,所以四边形$AEFD$是矩形,则$EF = AD = 2$米,$AE=DF = 1$米。
已知坡道$AB$的坡比为$1:1.5$,即$\frac{AE}{BE}=\frac{1}{1.5}$,因为$AE = 1$米,所以$BE=1.5$米。
已知$DC$的坡比为$1:2$,即$\frac{DF}{CF}=\frac{1}{2}$,因为$DF = 1$米,所以$CF = 2$米。
那么$BC=BE + EF+CF=1.5 + 2+2=5.5$米。
根据勾股定理,$AB=\sqrt{AE^{2}+BE^{2}}=\sqrt{1^{2}+1.5^{2}}=\sqrt{1 + 2.25}=\sqrt{3.25}=\frac{\sqrt{13}}{2}$米,$CD=\sqrt{DF^{2}+CF^{2}}=\sqrt{1^{2}+2^{2}}=\sqrt{1 + 4}=\sqrt{5}$米。
从点$C$滑到点$B$的总长度为$BC + AB+CD=5.5+\frac{\sqrt{13}}{2}+\sqrt{5}\approx5.5 + 1.80+2.24 = 9.54$米。
2. (2)
解:由(1)可知$BC = 5.5$米。
起跑线到墙的距离为$7$米,起跑线到点$C$以及点$B$到墙均需留出$1$米的距离,那么$BC + 1+1=5.5 + 2=7.5$米。
因为$7.5\gt7$,所以该场地不符合安全要求。
综上,(1)从点$C$滑到点$B$的总长度约为$9.54$米;(2)该场地不符合安全要求。

23. (10分)先阅读下列各式,再解决问题.
$\frac {1}{\sqrt {2}+1}= \frac {1×(\sqrt {2}-1)}{(\sqrt {2}+1)×(\sqrt {2}-1)}= \sqrt {2}-1;$
$\frac {1}{\sqrt {3}+\sqrt {2}}= \frac {1×(\sqrt {3}-\sqrt {2})}{(\sqrt {3}+\sqrt {2})×(\sqrt {3}-\sqrt {2})}= \sqrt {3}-\sqrt {2};$
$\frac {1}{\sqrt {5}+2}= \frac {1×(\sqrt {5}-2)}{(\sqrt {5}+2)×(\sqrt {5}-2)}= \sqrt {5}-2;$
…
(1)求$\frac {1}{\sqrt {7}+\sqrt {6}}$的值;
(2)求$\frac {1}{\sqrt {n+1}+\sqrt {n}}$(n为正整数)的值;
(3)求$\frac {1}{1+\sqrt {2}}+\frac {1}{\sqrt {2}+\sqrt {3}}+\frac {1}{\sqrt {3}+\sqrt {4}}+... +\frac {1}{\sqrt {2021}+\sqrt {2022}}+\frac {1}{\sqrt {2022}+\sqrt {2023}}$的值.
$\frac {1}{\sqrt {2}+1}= \frac {1×(\sqrt {2}-1)}{(\sqrt {2}+1)×(\sqrt {2}-1)}= \sqrt {2}-1;$
$\frac {1}{\sqrt {3}+\sqrt {2}}= \frac {1×(\sqrt {3}-\sqrt {2})}{(\sqrt {3}+\sqrt {2})×(\sqrt {3}-\sqrt {2})}= \sqrt {3}-\sqrt {2};$
$\frac {1}{\sqrt {5}+2}= \frac {1×(\sqrt {5}-2)}{(\sqrt {5}+2)×(\sqrt {5}-2)}= \sqrt {5}-2;$
…
(1)求$\frac {1}{\sqrt {7}+\sqrt {6}}$的值;
(2)求$\frac {1}{\sqrt {n+1}+\sqrt {n}}$(n为正整数)的值;
(3)求$\frac {1}{1+\sqrt {2}}+\frac {1}{\sqrt {2}+\sqrt {3}}+\frac {1}{\sqrt {3}+\sqrt {4}}+... +\frac {1}{\sqrt {2021}+\sqrt {2022}}+\frac {1}{\sqrt {2022}+\sqrt {2023}}$的值.
答案:
(1) $\frac{1}{\sqrt{7}+\sqrt{6}}=\frac{1×(\sqrt{7}-\sqrt{6})}{(\sqrt{7}+\sqrt{6})(\sqrt{7}-\sqrt{6})}=\sqrt{7}-\sqrt{6}$
(2) $\frac{1}{\sqrt{n+1}+\sqrt{n}}=\frac{1×(\sqrt{n+1}-\sqrt{n})}{(\sqrt{n+1}+\sqrt{n})(\sqrt{n+1}-\sqrt{n})}=\sqrt{n+1}-\sqrt{n}$
(3) $\frac{1}{1+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+\frac{1}{\sqrt{3}+\sqrt{4}}+\cdots+\frac{1}{\sqrt{2021}+\sqrt{2022}}+\frac{1}{\sqrt{2022}+\sqrt{2023}}$
$=\sqrt{2}-1+\sqrt{3}-\sqrt{2}+\sqrt{4}-\sqrt{3}+\cdots+\sqrt{2022}-\sqrt{2021}+\sqrt{2023}-\sqrt{2022}$
$=\sqrt{2023}-1$
(1) $\frac{1}{\sqrt{7}+\sqrt{6}}=\frac{1×(\sqrt{7}-\sqrt{6})}{(\sqrt{7}+\sqrt{6})(\sqrt{7}-\sqrt{6})}=\sqrt{7}-\sqrt{6}$
(2) $\frac{1}{\sqrt{n+1}+\sqrt{n}}=\frac{1×(\sqrt{n+1}-\sqrt{n})}{(\sqrt{n+1}+\sqrt{n})(\sqrt{n+1}-\sqrt{n})}=\sqrt{n+1}-\sqrt{n}$
(3) $\frac{1}{1+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+\frac{1}{\sqrt{3}+\sqrt{4}}+\cdots+\frac{1}{\sqrt{2021}+\sqrt{2022}}+\frac{1}{\sqrt{2022}+\sqrt{2023}}$
$=\sqrt{2}-1+\sqrt{3}-\sqrt{2}+\sqrt{4}-\sqrt{3}+\cdots+\sqrt{2022}-\sqrt{2021}+\sqrt{2023}-\sqrt{2022}$
$=\sqrt{2023}-1$
查看更多完整答案,请扫码查看


