第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
1. 下列图形中,既属于轴对称图形又属于中心对称图形的是(
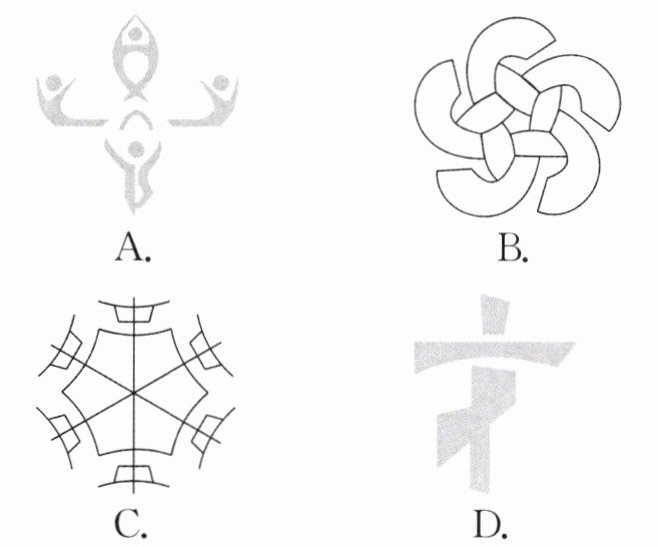
C
)
答案:
C
2. 若一个多边形的内角和等于$1260^{\circ }$,则该多边形的边数是(
A.8
B.9
C.10
D.11
B
)A.8
B.9
C.10
D.11
答案:
解:设该多边形的边数为$n$,根据多边形内角和公式$(n - 2)×180^{\circ}$,可得方程:
$(n - 2)×180^{\circ} = 1260^{\circ}$
$n - 2 = 1260^{\circ}÷180^{\circ}$
$n - 2 = 7$
$n = 9$
答案:B
$(n - 2)×180^{\circ} = 1260^{\circ}$
$n - 2 = 1260^{\circ}÷180^{\circ}$
$n - 2 = 7$
$n = 9$
答案:B
3. 用反证法证明“若$ab= 0$,则$a$,$b$中至少有一个为0”时,第一步应假设(
A.$a= 0$,$b= 0$
B.$a≠0$,$b≠0$
C.$a≠0$,$b= 0$
D.$a= 0$,$b≠0$
B
)A.$a= 0$,$b= 0$
B.$a≠0$,$b≠0$
C.$a≠0$,$b= 0$
D.$a= 0$,$b≠0$
答案:
用反证法证明“若$ab = 0$,则$a$,$b$中至少有一个为$0$”时,第一步应假设结论不成立,即“$a$,$b$中至少有一个为$0$”的反面“$a≠0$,$b≠0$”。
B
B
4. (泸州中考)如图,在$□ ABCD$中,$AE平分∠BAD$,交$BC于点E$,$∠D= 58^{\circ }$,则$∠AEC$的度数是(
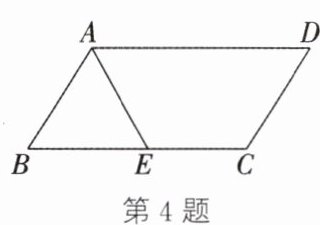
A.$61^{\circ }$
B.$109^{\circ }$
C.$119^{\circ }$
D.$122^{\circ }$
C
) 
A.$61^{\circ }$
B.$109^{\circ }$
C.$119^{\circ }$
D.$122^{\circ }$
答案:
解:
∵四边形ABCD是平行四边形,
∴AD//BC,∠BAD+∠D=180°,∠B=∠D=58°,
∴∠BAD=180°-∠D=180°-58°=122°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=122°÷2=61°,
∵AD//BC,
∴∠AEB=∠EAD=61°,
∵∠AEC+∠AEB=180°,
∴∠AEC=180°-∠AEB=180°-61°=119°.
答案:C
∵四边形ABCD是平行四边形,
∴AD//BC,∠BAD+∠D=180°,∠B=∠D=58°,
∴∠BAD=180°-∠D=180°-58°=122°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=122°÷2=61°,
∵AD//BC,
∴∠AEB=∠EAD=61°,
∵∠AEC+∠AEB=180°,
∴∠AEC=180°-∠AEB=180°-61°=119°.
答案:C
5. 如图,在$□ ABCD$中,对角线$AC$,$BD相交于点O$,$OE⊥BD交AD于点E$,连结$BE$。若$□ ABCD$的周长为28,则$\triangle ABE$的周长为(
A.28
B.24
C.21
D.14
D
)A.28
B.24
C.21
D.14
答案:
解:
∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AD=BC。
∵平行四边形ABCD的周长为28,
∴AB+AD=14。
∵OE⊥BD,OB=OD,
∴OE垂直平分BD,
∴BE=DE。
∴△ABE的周长=AB+AE+BE=AB+AE+DE=AB+AD=14。
答案:D
∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AD=BC。
∵平行四边形ABCD的周长为28,
∴AB+AD=14。
∵OE⊥BD,OB=OD,
∴OE垂直平分BD,
∴BE=DE。
∴△ABE的周长=AB+AE+BE=AB+AE+DE=AB+AD=14。
答案:D
6. (达州中考)如图,在$\triangle ABC$中,$D$,$E分别是边AB$,$BC$的中点,点$F在DE$的延长线上,连结$CF$。若添加一个条件,使得四边形$ADFC$为平行四边形,则这个条件可以是(
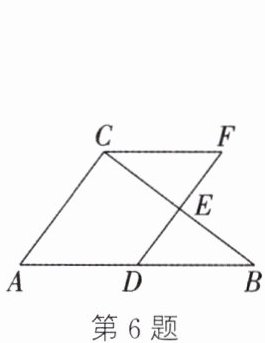
A.$∠B= ∠F$
B.$DE= EF$
C.$AC= CF$
D.$AD= CF$
B
)
A.$∠B= ∠F$
B.$DE= EF$
C.$AC= CF$
D.$AD= CF$
答案:
解:
∵D,E分别是AB,BC的中点,
∴DE是△ABC的中位线,
∴DE//AC,DE = $\frac{1}{2}$AC。
若添加条件DE = EF,则DF = DE + EF = 2DE = AC。
∵DE//AC,即DF//AC,且DF = AC,
∴四边形ADFC为平行四边形。
答案:B
∵D,E分别是AB,BC的中点,
∴DE是△ABC的中位线,
∴DE//AC,DE = $\frac{1}{2}$AC。
若添加条件DE = EF,则DF = DE + EF = 2DE = AC。
∵DE//AC,即DF//AC,且DF = AC,
∴四边形ADFC为平行四边形。
答案:B
7. (嘉兴中考)如图,在$\triangle ABC$中,$AB= AC= 8$,点$E$,$F$,$G分别在边AB$,$BC$,$AC$上,且$EF// AC$,$GF// AB$,则四边形$AEFG$的周长是(
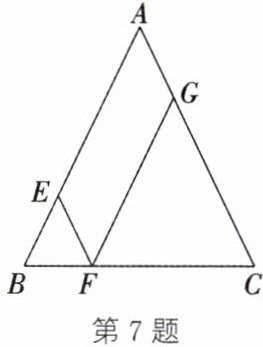
A.8
B.16
C.24
D.32
B
)
A.8
B.16
C.24
D.32
答案:
B 解析:
∵EF//AC,GF//AB,
∴四边形AEFG是平行四边形,∠B = ∠GFC,∠C = ∠EFB。
∵AB = AC,
∴∠B = ∠C。
∴∠B = ∠EFB,∠GFC = ∠C。
∴EB = EF,FG = GC。
∵四边形AEFG的周长 = AE + EF + FG + AG,
∴四边形AEFG的周长 = AE + EB + GC + AG = AB + AC。
∵AB = AC = 8,
∴四边形AEFG的周长 = AB + AC = 8 + 8 = 16。
∵EF//AC,GF//AB,
∴四边形AEFG是平行四边形,∠B = ∠GFC,∠C = ∠EFB。
∵AB = AC,
∴∠B = ∠C。
∴∠B = ∠EFB,∠GFC = ∠C。
∴EB = EF,FG = GC。
∵四边形AEFG的周长 = AE + EF + FG + AG,
∴四边形AEFG的周长 = AE + EB + GC + AG = AB + AC。
∵AB = AC = 8,
∴四边形AEFG的周长 = AB + AC = 8 + 8 = 16。
8. 如图,分别以$Rt\triangle ABC的斜边AB和直角边AC为边向\triangle ABC外作等边三角形ABD和等边三角形ACE$,$F为AB$的中点,$DE与AB交于点G$,$EF与AC交于点H$,$∠ACB= 90^{\circ }$,$∠BAC= 30^{\circ }$。给出下列结论:①$EF⊥AC$;②$BD= 4FH$;③四边形$ADFE$为平行四边形;④$AD= 4AG$。其中,正确的是(
A.①③④
B.①②③
C.①②④
D.①②③④
D
)A.①③④
B.①②③
C.①②④
D.①②③④
答案:
D 解析:
∵△ACE是等边三角形,
∴∠EAC = 60°,AE = AC。
∵∠BAC = 30°,
∴∠EAF = 90°。
∵∠ACB = 90°,∠BAC = 30°,
∴易得AB = 2BC。
∵F为AB的中点,
∴AB = 2FA。
∴BC = FA。在△ABC和△EFA中,
∵$\begin{cases}AC = EA\\\angle ACB = \angle EAF = 90^{\circ}\\BC = FA\end{cases}$,
∴△ABC≌△EFA。
∴AB = EF,∠BAC = ∠FEA = 30°。
∴∠AHE = 180° - ∠EAC - ∠FEA = 180° - 60° - 30° = 90°。
∴EF⊥AC。故①正确。
∵△ACE为等边三角形,EF⊥AC,
∴H为AC的中点,又
∵F为AB的中点,
∴FH是△ABC的中位线,
∴FH = $\frac{1}{2}$BC。
∵BC = $\frac{1}{2}$AB,
∴AB = 4FH。
∵△ABD是等边三角形,
∴AB = BD = AD。
∴BD = 4FH。故②正确。
∵AD = BD,BF = FA,
∴易得∠DFB = 90°,∠BDF = 30°。
∵∠EAF = 90°,
∴∠DFB = ∠EAF。
∵∠FEA = 30°,
∴∠BDF = ∠FEA。在△DBF和△EFA中,
∵$\begin{cases}\angle BDF = \angle FEA\\\angle DFB = \angle EAF\\BF = FA\end{cases}$,
∴△DBF≌△EFA。
∴DF = EA。
∵EF = AB = AD,
∴四边形ADFE为平行四边形。故③正确。
∵四边形ADFE为平行四边形,
∴AG = $\frac{1}{2}$AF。
∴AG = $\frac{1}{4}$AB。
∵AD = AB,
∴AD = 4AG。故④正确。综上所述,正确的是①②③④。
∵△ACE是等边三角形,
∴∠EAC = 60°,AE = AC。
∵∠BAC = 30°,
∴∠EAF = 90°。
∵∠ACB = 90°,∠BAC = 30°,
∴易得AB = 2BC。
∵F为AB的中点,
∴AB = 2FA。
∴BC = FA。在△ABC和△EFA中,
∵$\begin{cases}AC = EA\\\angle ACB = \angle EAF = 90^{\circ}\\BC = FA\end{cases}$,
∴△ABC≌△EFA。
∴AB = EF,∠BAC = ∠FEA = 30°。
∴∠AHE = 180° - ∠EAC - ∠FEA = 180° - 60° - 30° = 90°。
∴EF⊥AC。故①正确。
∵△ACE为等边三角形,EF⊥AC,
∴H为AC的中点,又
∵F为AB的中点,
∴FH是△ABC的中位线,
∴FH = $\frac{1}{2}$BC。
∵BC = $\frac{1}{2}$AB,
∴AB = 4FH。
∵△ABD是等边三角形,
∴AB = BD = AD。
∴BD = 4FH。故②正确。
∵AD = BD,BF = FA,
∴易得∠DFB = 90°,∠BDF = 30°。
∵∠EAF = 90°,
∴∠DFB = ∠EAF。
∵∠FEA = 30°,
∴∠BDF = ∠FEA。在△DBF和△EFA中,
∵$\begin{cases}\angle BDF = \angle FEA\\\angle DFB = \angle EAF\\BF = FA\end{cases}$,
∴△DBF≌△EFA。
∴DF = EA。
∵EF = AB = AD,
∴四边形ADFE为平行四边形。故③正确。
∵四边形ADFE为平行四边形,
∴AG = $\frac{1}{2}$AF。
∴AG = $\frac{1}{4}$AB。
∵AD = AB,
∴AD = 4AG。故④正确。综上所述,正确的是①②③④。
9. (眉山中考)若一个多边形的外角和是内角和的$\frac {2}{9}$,则这个多边形的边数为______
11
。
答案:
解:设这个多边形的边数为$n$。
多边形内角和公式为$(n - 2)×180°$,任意多边形外角和为$360°$。
由题意得:$360° = \frac{2}{9}×(n - 2)×180°$
化简得:$360 = \frac{2}{9}×180×(n - 2)$
$360 = 40×(n - 2)$
$n - 2 = 9$
$n = 11$
11
多边形内角和公式为$(n - 2)×180°$,任意多边形外角和为$360°$。
由题意得:$360° = \frac{2}{9}×(n - 2)×180°$
化简得:$360 = \frac{2}{9}×180×(n - 2)$
$360 = 40×(n - 2)$
$n - 2 = 9$
$n = 11$
11
查看更多完整答案,请扫码查看


