第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
1. 下列各式中,计算正确的是(
A.$\sqrt{2}+\sqrt{3}= \sqrt{5}$
B.$4\sqrt{3}-3\sqrt{3}= 1$
C.$\sqrt{2}×\sqrt{3}= \sqrt{6}$
D.$\sqrt{12}÷2= \sqrt{6}$
C
)A.$\sqrt{2}+\sqrt{3}= \sqrt{5}$
B.$4\sqrt{3}-3\sqrt{3}= 1$
C.$\sqrt{2}×\sqrt{3}= \sqrt{6}$
D.$\sqrt{12}÷2= \sqrt{6}$
答案:
A. $\sqrt{2}$与$\sqrt{3}$不是同类二次根式,不能合并,故A错误;
B. $4\sqrt{3}-3\sqrt{3}=\sqrt{3}$,故B错误;
C. $\sqrt{2}×\sqrt{3}=\sqrt{2×3}=\sqrt{6}$,故C正确;
D. $\sqrt{12}÷2=2\sqrt{3}÷2=\sqrt{3}$,故D错误。
结论:C
B. $4\sqrt{3}-3\sqrt{3}=\sqrt{3}$,故B错误;
C. $\sqrt{2}×\sqrt{3}=\sqrt{2×3}=\sqrt{6}$,故C正确;
D. $\sqrt{12}÷2=2\sqrt{3}÷2=\sqrt{3}$,故D错误。
结论:C
2. (雅安中考)若直角三角形的两边长分别是方程$x^{2}-7x+12= 0$的两根,则该直角三角形的面积是(
A.6
B.12
C.12 或$\frac{3\sqrt{7}}{2}$
D.6 或$\frac{3\sqrt{7}}{2}$
D
)A.6
B.12
C.12 或$\frac{3\sqrt{7}}{2}$
D.6 或$\frac{3\sqrt{7}}{2}$
答案:
解:解方程$x^{2}-7x+12=0$,
因式分解得$(x-3)(x-4)=0$,
解得$x_1=3$,$x_2=4$。
情况一:当3和4为直角边时,
面积$S=\frac{1}{2}×3×4=6$。
情况二:当4为斜边,3为直角边时,
另一直角边$a=\sqrt{4^{2}-3^{2}}=\sqrt{7}$,
面积$S=\frac{1}{2}×3×\sqrt{7}=\frac{3\sqrt{7}}{2}$。
综上,该直角三角形的面积是6或$\frac{3\sqrt{7}}{2}$。
答案:D
因式分解得$(x-3)(x-4)=0$,
解得$x_1=3$,$x_2=4$。
情况一:当3和4为直角边时,
面积$S=\frac{1}{2}×3×4=6$。
情况二:当4为斜边,3为直角边时,
另一直角边$a=\sqrt{4^{2}-3^{2}}=\sqrt{7}$,
面积$S=\frac{1}{2}×3×\sqrt{7}=\frac{3\sqrt{7}}{2}$。
综上,该直角三角形的面积是6或$\frac{3\sqrt{7}}{2}$。
答案:D
3. (黔东南中考)已知关于 x 的一元二次方程$x^{2}-2x-a= 0的两个实数根分别为x_{1},x_{2}$.若$x_{1}= -1$,则$a-x_{1}^{2}-x_{2}^{2}$的值为(
A.7
B.-7
C.6
D.-6
B
)A.7
B.-7
C.6
D.-6
答案:
解:
∵$x_{1}=-1$是方程$x^{2}-2x-a=0$的根,
∴$(-1)^{2}-2×(-1)-a=0$,解得$a=3$。
原方程为$x^{2}-2x-3=0$,
由韦达定理得$x_{1}+x_{2}=2$,$x_{1}x_{2}=-3$。
$x_{1}^{2}+x_{2}^{2}=(x_{1}+x_{2})^{2}-2x_{1}x_{2}=2^{2}-2×(-3)=4+6=10$。
$a-x_{1}^{2}-x_{2}^{2}=3-10=-7$。
答案:B
∵$x_{1}=-1$是方程$x^{2}-2x-a=0$的根,
∴$(-1)^{2}-2×(-1)-a=0$,解得$a=3$。
原方程为$x^{2}-2x-3=0$,
由韦达定理得$x_{1}+x_{2}=2$,$x_{1}x_{2}=-3$。
$x_{1}^{2}+x_{2}^{2}=(x_{1}+x_{2})^{2}-2x_{1}x_{2}=2^{2}-2×(-3)=4+6=10$。
$a-x_{1}^{2}-x_{2}^{2}=3-10=-7$。
答案:B
4. (恩施中考)为了了解某小区居民的用水情况,随机抽查了若干户家庭某月的用水量,统计结果如下表:
|月用水量(吨)|3|4|5|6|
|户 数|4|6|8|2|
关于若干户家庭该月的用水量,下列说法正确的(
A.众数是 5 吨
B.平均数是 7 吨
C.中位数是 5 吨
D.方差是 1 吨$^2$
|月用水量(吨)|3|4|5|6|
|户 数|4|6|8|2|
关于若干户家庭该月的用水量,下列说法正确的(
A
)A.众数是 5 吨
B.平均数是 7 吨
C.中位数是 5 吨
D.方差是 1 吨$^2$
答案:
解:
A. 众数是5吨(出现8次,次数最多),正确;
B. 平均数:$\frac{3×4 + 4×6 + 5×8 + 6×2}{4 + 6 + 8 + 2} = \frac{12 + 24 + 40 + 12}{20} = \frac{88}{20} = 4.4$吨,错误;
C. 共20户,中位数是第10、11户的平均数,第10户4吨,第11户5吨,中位数$\frac{4 + 5}{2} = 4.5$吨,错误;
D. 方差:$\frac{4×(3 - 4.4)^2 + 6×(4 - 4.4)^2 + 8×(5 - 4.4)^2 + 2×(6 - 4.4)^2}{20} = \frac{4×1.96 + 6×0.16 + 8×0.36 + 2×2.56}{20} = \frac{7.84 + 0.96 + 2.88 + 5.12}{20} = \frac{16.8}{20} = 0.84$吨²,错误。
答案:A
A. 众数是5吨(出现8次,次数最多),正确;
B. 平均数:$\frac{3×4 + 4×6 + 5×8 + 6×2}{4 + 6 + 8 + 2} = \frac{12 + 24 + 40 + 12}{20} = \frac{88}{20} = 4.4$吨,错误;
C. 共20户,中位数是第10、11户的平均数,第10户4吨,第11户5吨,中位数$\frac{4 + 5}{2} = 4.5$吨,错误;
D. 方差:$\frac{4×(3 - 4.4)^2 + 6×(4 - 4.4)^2 + 8×(5 - 4.4)^2 + 2×(6 - 4.4)^2}{20} = \frac{4×1.96 + 6×0.16 + 8×0.36 + 2×2.56}{20} = \frac{7.84 + 0.96 + 2.88 + 5.12}{20} = \frac{16.8}{20} = 0.84$吨²,错误。
答案:A
5. 如图,$□ ABCD$的周长为 14,$BE= 2$,AE 平分$∠BAD$,交边 BC 于点 E,则 CE 的长为(
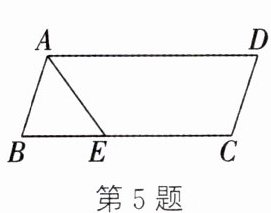
A.1
B.2
C.3
D.4
C
) 
A.1
B.2
C.3
D.4
答案:
解:
∵四边形ABCD是平行四边形,
∴AD//BC,AB=CD,AD=BC,
∴∠DAE=∠BEA。
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠BEA,
∴AB=BE=2。
∵□ABCD的周长为14,
∴2(AB+BC)=14,即AB+BC=7,
∴BC=7-AB=7-2=5,
∴CE=BC-BE=5-2=3。
答案:C
∵四边形ABCD是平行四边形,
∴AD//BC,AB=CD,AD=BC,
∴∠DAE=∠BEA。
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠BEA,
∴AB=BE=2。
∵□ABCD的周长为14,
∴2(AB+BC)=14,即AB+BC=7,
∴BC=7-AB=7-2=5,
∴CE=BC-BE=5-2=3。
答案:C
6. 如图,在矩形 ABCD 中无重叠地放入面积分别为$8cm^{2}和12cm^{2}$的两张正方形纸片,则剩余部分的面积为(
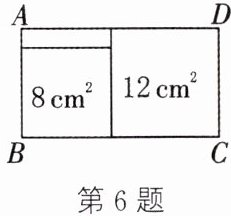
A.$4\sqrt{3}cm^{2}$
B.$(8\sqrt{3}-12)cm^{2}$
C.$(4\sqrt{6}-8)cm^{2}$
D.$(4\sqrt{6}+12)cm^{2}$
C
) 
A.$4\sqrt{3}cm^{2}$
B.$(8\sqrt{3}-12)cm^{2}$
C.$(4\sqrt{6}-8)cm^{2}$
D.$(4\sqrt{6}+12)cm^{2}$
答案:
C 解析:
∵ 两张正方形纸片的面积分别为 $12cm^{2}$ 和 $8cm^{2}$,
∴ 它们的边长分别为 $2\sqrt{3}cm$, $2\sqrt{2}cm$.
∴ $AB = 2\sqrt{3}cm$, $BC=(2\sqrt{3}+2\sqrt{2})cm$.
∴ 剩余部分的面积 $=2\sqrt{3}×(2\sqrt{3}+2\sqrt{2})-12 - 8=(4\sqrt{6}-8)cm^{2}$.
∵ 两张正方形纸片的面积分别为 $12cm^{2}$ 和 $8cm^{2}$,
∴ 它们的边长分别为 $2\sqrt{3}cm$, $2\sqrt{2}cm$.
∴ $AB = 2\sqrt{3}cm$, $BC=(2\sqrt{3}+2\sqrt{2})cm$.
∴ 剩余部分的面积 $=2\sqrt{3}×(2\sqrt{3}+2\sqrt{2})-12 - 8=(4\sqrt{6}-8)cm^{2}$.
7. (武汉中考)已知点$A(x_{1},y_{1}),B(x_{2},y_{2})在反比例函数y= \frac{6}{x}$的图象上,且$x_{1}<0<x_{2}$,则下列结论中,一定正确的是(
A.$y_{1}+y_{2}<0$
B.$y_{1}+y_{2}>0$
C.$y_{1}<y_{2}$
D.$y_{1}>y_{2}$
C
)A.$y_{1}+y_{2}<0$
B.$y_{1}+y_{2}>0$
C.$y_{1}<y_{2}$
D.$y_{1}>y_{2}$
答案:
C 解析:在 $y=\frac{6}{x}$ 中,
∵ $6>0$,
∴ 该反比例函数的图象位于一、三象限,且在每个象限内,y 随 x 的增大而减小.
∵ 点 $A(x_{1},y_{1})$, $B(x_{2},y_{2})$ 在反比例函数 $y=\frac{6}{x}$ 的图象上,且 $x_{1}<0<x_{2}$,
∴ 点 A 位于第三象限,点 B 位于第一象限.
∴ $y_{1}<y_{2}$.
∵ $6>0$,
∴ 该反比例函数的图象位于一、三象限,且在每个象限内,y 随 x 的增大而减小.
∵ 点 $A(x_{1},y_{1})$, $B(x_{2},y_{2})$ 在反比例函数 $y=\frac{6}{x}$ 的图象上,且 $x_{1}<0<x_{2}$,
∴ 点 A 位于第三象限,点 B 位于第一象限.
∴ $y_{1}<y_{2}$.
8. 如图,在平面直角坐标系中,O 为坐标原点,$\triangle ABO$的顶点 B 在反比例函数$y= \frac{3}{x}(x>0)$的图象上,顶点 A 在反比例函数$y= \frac{-2}{x}(x<0)$的图象上,则$\triangle ABO$的面积是(
A.2
B.1
C.3
D.$\frac{5}{2}$
D
)A.2
B.1
C.3
D.$\frac{5}{2}$
答案:
D 解析:由题意,得 $S_{\triangle ABO}=\frac{3}{2}+\frac{|-2|}{2}=\frac{5}{2}$.
9. 如图,在$□ ABCD$中,对角线 AC,BD 相交于点 O,$BD= 2AD$,E,F,G 分别是 OC,OD,AB 的中点. 有下列结论:① 四边形 BEFG 是平行四边形;② $BE⊥AC$;③ $EG= FG$;④ EA 平分$∠GEF$.其中,正确的是(
A.①②
B.①②③
C.①②④
D.①③④
C
)A.①②
B.①②③
C.①②④
D.①③④
答案:
C 解析:
∵ 四边形 ABCD 是平行四边形,
∴ $BO = DO=\frac{1}{2}BD$, $AD = BC$, $AB = CD$, $AB// CD$. 又
∵ $BD = 2AD$,
∴ $OB = BC = OD = DA$.
∵ E 是 OC 的中点,
∴ $BE\perp AC$. 故②正确.
∵ E,F 分别是 OC,OD 的中点,
∴ EF 是 $\triangle OCD$ 的中位线.
∴ $EF// CD$, $EF=\frac{1}{2}CD=\frac{1}{2}AB$.
∴ $EF// AB$.
∵ G 是 $Rt\triangle ABE$ 斜边 AB 的中点,
∴ $EG=\frac{1}{2}AB = AG = BG$.
∴ $EG = EF = AG = BG$.
∴ 四边形 BEFG 是平行四边形. 故①正确. 无法证明 $EG = FG$, 故③错误.
∵ $EF// CD// AB$,
∴ $\angle BAC=\angle ACD=\angle AEF$.
∵ $AG = EG$,
∴ $\angle GAE=\angle AEG$.
∴ $\angle AEG=\angle AEF$.
∴ EA 平分 $\angle GEF$. 故④正确. 综上所述,正确的是①②④.
∵ 四边形 ABCD 是平行四边形,
∴ $BO = DO=\frac{1}{2}BD$, $AD = BC$, $AB = CD$, $AB// CD$. 又
∵ $BD = 2AD$,
∴ $OB = BC = OD = DA$.
∵ E 是 OC 的中点,
∴ $BE\perp AC$. 故②正确.
∵ E,F 分别是 OC,OD 的中点,
∴ EF 是 $\triangle OCD$ 的中位线.
∴ $EF// CD$, $EF=\frac{1}{2}CD=\frac{1}{2}AB$.
∴ $EF// AB$.
∵ G 是 $Rt\triangle ABE$ 斜边 AB 的中点,
∴ $EG=\frac{1}{2}AB = AG = BG$.
∴ $EG = EF = AG = BG$.
∴ 四边形 BEFG 是平行四边形. 故①正确. 无法证明 $EG = FG$, 故③错误.
∵ $EF// CD// AB$,
∴ $\angle BAC=\angle ACD=\angle AEF$.
∵ $AG = EG$,
∴ $\angle GAE=\angle AEG$.
∴ $\angle AEG=\angle AEF$.
∴ EA 平分 $\angle GEF$. 故④正确. 综上所述,正确的是①②④.
10. 如图,在正方形 ABCD 中,点 E 从点 B 出发,沿 BC 方向向终点 C 运动,$DF⊥AE$交 AB 于点 F,连结 FE,以 FD,FE 为邻边构造$□ DFEP$,连结 CP,则$∠DFE+∠EPC$的度数的变化情况是( )
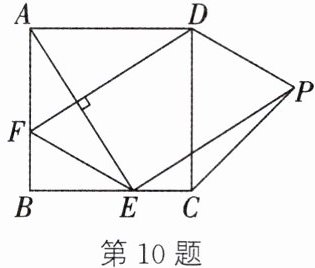
A.一直减小
B.一直减小后增大
C.一直不变
D.先增大后减小

A.一直减小
B.一直减小后增大
C.一直不变
D.先增大后减小
答案:
A 解析:如图,过点 P 作 $PH\perp BC$, 交 BC 的延长线于点 H, 则 $\angle H = 90^{\circ}$.
∵ 四边形 ABCD 是正方形,
∴ $AD = AB = BC$, $\angle DAF=\angle B=\angle DCB = 90^{\circ}$.
∴ $\angle DCH = 90^{\circ}$, $\angle BAE+\angle DAE = 90^{\circ}$.
∵ $DF\perp AE$,
∴ $\angle ADF+\angle DAE = 90^{\circ}$.
∴ $\angle ADF=\angle BAE$.
∴ $\triangle ADF\cong\triangle BAE$.
∴ $DF = AE$.
∵ 四边形 DFEP 是平行四边形,
∴ $DF// EP$, $DF = EP$, $\angle DFE=\angle DPE$.
∴ $AE = DF = EP$.
∵ $\angle B = 90^{\circ}$,
∴ $\angle BAE+\angle AEB = 90^{\circ}$.
∵ $DF\perp AE$,
∴ $PE\perp AE$.
∴ $\angle AEP = 90^{\circ}$.
∴ $\angle AEB+\angle PEH = 90^{\circ}$.
∴ $\angle BAE=\angle HEP$.
∵ $\angle ABE=\angle H = 90^{\circ}$, $AE = EP$,
∴ $\triangle ABE\cong\triangle EHP$.
∴ $BE = HP$, $AB = EH = BC$.
∴ $BE = BC - CE = EH - CE = CH$.
∴ $HP = CH$.
∴ 易得 $\angle PCH = 45^{\circ}$.
∵ $\angle DCH = 90^{\circ}$,
∴ $\angle DCP = 45^{\circ}=\angle PCH$.
∴ CP 是 $\angle DCH$ 的平分线.
∴ 点 P 在 $\angle DCH$ 的平分线上运动.
∵ $\angle DFE=\angle DPE$,
∴ $\angle DFE+\angle EPC=\angle DPE+\angle EPC=\angle DPC$.
∵ 点 E 从点 B 出发, 沿 BC 方向向终点 C 运动时, $\angle DCP$ 的度数不变, $\angle CDP$ 的度数变大, $\angle DPC = 180^{\circ}-\angle DCP-\angle CDP$,
∴ $\angle DPC$ 的度数变小.
∴ $\angle DFE+\angle EPC$ 的度数一直减小.

A 解析:如图,过点 P 作 $PH\perp BC$, 交 BC 的延长线于点 H, 则 $\angle H = 90^{\circ}$.
∵ 四边形 ABCD 是正方形,
∴ $AD = AB = BC$, $\angle DAF=\angle B=\angle DCB = 90^{\circ}$.
∴ $\angle DCH = 90^{\circ}$, $\angle BAE+\angle DAE = 90^{\circ}$.
∵ $DF\perp AE$,
∴ $\angle ADF+\angle DAE = 90^{\circ}$.
∴ $\angle ADF=\angle BAE$.
∴ $\triangle ADF\cong\triangle BAE$.
∴ $DF = AE$.
∵ 四边形 DFEP 是平行四边形,
∴ $DF// EP$, $DF = EP$, $\angle DFE=\angle DPE$.
∴ $AE = DF = EP$.
∵ $\angle B = 90^{\circ}$,
∴ $\angle BAE+\angle AEB = 90^{\circ}$.
∵ $DF\perp AE$,
∴ $PE\perp AE$.
∴ $\angle AEP = 90^{\circ}$.
∴ $\angle AEB+\angle PEH = 90^{\circ}$.
∴ $\angle BAE=\angle HEP$.
∵ $\angle ABE=\angle H = 90^{\circ}$, $AE = EP$,
∴ $\triangle ABE\cong\triangle EHP$.
∴ $BE = HP$, $AB = EH = BC$.
∴ $BE = BC - CE = EH - CE = CH$.
∴ $HP = CH$.
∴ 易得 $\angle PCH = 45^{\circ}$.
∵ $\angle DCH = 90^{\circ}$,
∴ $\angle DCP = 45^{\circ}=\angle PCH$.
∴ CP 是 $\angle DCH$ 的平分线.
∴ 点 P 在 $\angle DCH$ 的平分线上运动.
∵ $\angle DFE=\angle DPE$,
∴ $\angle DFE+\angle EPC=\angle DPE+\angle EPC=\angle DPC$.
∵ 点 E 从点 B 出发, 沿 BC 方向向终点 C 运动时, $\angle DCP$ 的度数不变, $\angle CDP$ 的度数变大, $\angle DPC = 180^{\circ}-\angle DCP-\angle CDP$,
∴ $\angle DPC$ 的度数变小.
∴ $\angle DFE+\angle EPC$ 的度数一直减小.

查看更多完整答案,请扫码查看


