《2025年暑期升级训练八年级数学浙教版浙江教育出版社》

7. 已知二次函数 $ y = x ^ { 2 } - 3 x + 3 $,当 $ t \leq x \leq t + 1 $ 时,有最小值 $ t $,则 $ t $ 的值是(D)
A.$ 1 $
B.$ 3 $
C.$ \frac { 3 } { 4 } $ 或 $ 1 $
D.$ \frac { 3 } { 4 } $ 或 $ 3 $

答案： D 解析：配方，得 $ y = ( x - \frac { 3 } { 2 } ) ^ { 2 } + \frac { 3 } { 4 } $。分情况讨论：① 若对称轴在 $ t \leqslant x \leqslant t + 1 $ 对应图象的右侧，则 $ t + 1 ＜ \frac { 3 } { 2 } $，即 $ t ＜ \frac { 1 } { 2 } $。当 $ t \leqslant x \leqslant t + 1 $ 时，$ y $ 随 $ x $ 的增大而减小，
∴ 当 $ x = t + 1 $ 时，函数取得最小值，即 $ t = ( t + 1 ) ^ { 2 } - 3 ( t + 1 ) + 3 $，解得 $ t _ { 1 } = t _ { 2 } = 1 $（不合题意，舍去）。② 若对称轴在 $ t \leqslant x \leqslant t + 1 $ 对应图象内，则 $ t \leqslant \frac { 3 } { 2 } \leqslant t + 1 $，解得 $ \frac { 1 } { 2 } \leqslant t \leqslant \frac { 3 } { 2 } $。当 $ x = \frac { 3 } { 2 } $ 时，函数取得最小值，即 $ t = \frac { 3 } { 4 } $。③ 若对称轴在 $ t \leqslant x \leqslant t + 1 $ 对应图象的左侧，则 $ t ＞ \frac { 3 } { 2 } $。当 $ t \leqslant x \leqslant t + 1 $ 时，$ y $ 随 $ x $ 的增大而增大。
∴ 当 $ x = t $ 时，函数取得最小值，即 $ t = t ^ { 2 } - 3 t + 3 $，解得 $ t _ { 1 } = 3 $，$ t _ { 2 } = 1 $（不合题意，舍去）。综上所述，$ t $ 的值为 $ \frac { 3 } { 4 } $ 或 $ 3 $。

8. 如图,在边长为 $ 6 \mathrm { cm } $ 的正方形 $ A B C D $ 中,点 $ E $,$ F $,$ G $,$ H $ 分别从点 $ A $,$ B $,$ C $,$ D $ 同时出发,均以 $ 1 \mathrm { cm } / \mathrm { s } $ 的速度向点 $ B $,$ C $,$ D $,$ A $ 匀速运动,当点 $ E $ 到达点 $ B $ 时,四个点同时停止运动. 在运动过程中,当运动时间为3$ \mathrm { s } $ 时,四边形 $ E F G H $ 的面积最小,最小面积是18$ \mathrm { cm } ^ { 2 } $.

答案： 设运动时间为 $ t \, \text{s} $，四边形 $ EFGH $ 的面积为 $ S \, \text{cm}^2 $。
由题意得：$ AE = t \, \text{cm} $，$ AH = (6 - t) \, \text{cm} $。
正方形 $ ABCD $ 的面积为 $ 6^2 = 36 \, \text{cm}^2 $。
$\triangle AEH$ 的面积为 $ \frac{1}{2} × AE × AH = \frac{1}{2}t(6 - t) \, \text{cm}^2 $。
由对称性可知，四个三角形面积相等，故四边形 $ EFGH $ 的面积：
$\begin{aligned}S &= 36 - 4 × \frac{1}{2}t(6 - t) \\&= 36 - 2t(6 - t) \\&= 36 - 12t + 2t^2 \\&= 2t^2 - 12t + 36 \\&= 2(t^2 - 6t + 9) + 18 \\&= 2(t - 3)^2 + 18\end{aligned}$
$\because 2 ＞ 0$，$\therefore$ 当 $ t = 3 $ 时，$ S $ 取得最小值，最小值为 $ 18 \, \text{cm}^2 $。
$3$；$18$

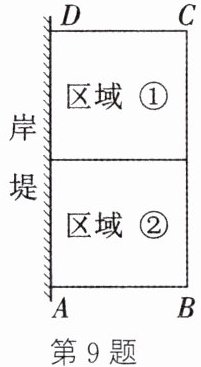
9. 为了节省材料,某水产养殖户利用水库的岸堤为一边,用总长为 $ a $ 米($ a $ 为大于 $ 21 $ 的常数)的围网在水库中围成了如图所示的两块矩形区域①②. 已知岸堤的可用长度不超过 $ 21 $ 米. 设 $ A B $ 的长为 $ x $ 米,矩形 $ A B C D $ 的面积为 $ y $ 平方米.
(1) 求 $ y $ 与 $ x $ 之间的函数表达式,并直接写出自变量 $ x $ 的取值范围(用含 $ a $ 的式子表示)；
(2) 若 $ a = 30 $,求 $ y $ 的最大值,并求出此时 $ x $ 的值；
(3) 若 $ a = 48 $,求 $ y $ 的最大值.

答案： （1）解：由题意得，$BC$的长为$(a - 3x)$米，
则$y = x(a - 3x) = -3x^2 + ax$，
因为$a - 3x \leq 21$，所以$x \geq \frac{a - 21}{3}$，
因为$a - 3x ＞ 0$，所以$x ＜ \frac{a}{3}$，
自变量$x$的取值范围是$\frac{a - 21}{3} \leq x ＜ \frac{a}{3}$。
（2）解：当$a = 30$时，$y = -3x^2 + 30x = -3(x - 5)^2 + 75$，
由（1）知，自变量$x$的取值范围是$3 \leq x ＜ 10$，
所以当$x = 5$时，$y$有最大值$75$。
（3）解：当$a = 48$时，$y = -3x^2 + 48x = -3(x - 8)^2 + 192$，
由（1）知，自变量$x$的取值范围是$9 \leq x ＜ 16$，
所以当$x = 9$时，$y$有最大值$189$。

10. 如图,利用一面墙(墙的长度足够),用篱笆围成一个矩形场地 $ A B C D $,在边 $ A D $,$ B C $ 上各有一个长为 $ 1 \mathrm { m } $ 的缺口,在场地中有用篱笆做的隔断 $ E F $,且 $ E F \perp A B $,$ A B ＞ E F $. 已知所用篱笆的总长度为 $ 38 \mathrm { m } $,设隔断 $ E F $ 的长为 $ x \mathrm { m } $.
(1) 请用含 $ x $ 的代数式表示 $ A B $ 的长.
(2) 若所围成的矩形场地 $ A B C D $ 的面积为 $ 100 \mathrm { m } ^ { 2 } $,求 $ A B $ 的长.
(3) 所围成的矩形场地 $ A B C D $ 的面积能否为 $ 140 \mathrm { m } ^ { 2 } $？若能,求 $ A B $ 的长；若不能,说明理由. 写出所围成的矩形场地 $ A B C D $ 的最大面积.

答案： （1）设隔断$EF$的长为$x\ \text{m}$，则$AD=BC=EF=x\ \text{m}$，由于$AD$，$BC$上各有一个长为$1\ \text{m}$的缺口，所以$AD$，$BC$上实际篱笆长度均为$(x - 1)\ \text{m}$，$EF$的长度为$x\ \text{m}$，设$AB=y\ \text{m}$，则篱笆总长度为$AB + 2(AD - 1) + EF = y + 2(x - 1) + x = 38$，整理得$y = 38 - x - 2(x - 1) = 40 - 3x$，故$AB=(40 - 3x)\ \text{m}$。
（2）矩形面积$S = AB × AD = x(40 - 3x)$，当$S = 100$时，$x(40 - 3x)=100$，整理得$3x^2 - 40x + 100 = 0$，解得$x_1 = 10$，$x_2=\frac{10}{3}$。因为$AB＞EF$，所以$40 - 3x ＞ x$，即$x ＜ 10$，又$x - 1 ＞ 0$，即$x ＞ 1$，所以$1 ＜ x ＜ 10$，故$x=\frac{10}{3}$，则$AB = 40 - 3×\frac{10}{3}=30\ \text{m}$。
（3）不能。当$S = 140$时，$x(40 - 3x)=140$，整理得$3x^2 - 40x + 140 = 0$，$\Delta=(-40)^2 - 4×3×140=1600 - 1680=-80 ＜ 0$，方程无实数根，故面积不能为$140\ \text{m}^2$。$S=-3x^2 + 40x=-3\left(x - \frac{20}{3}\right)^2+\frac{400}{3}$，因为$1 ＜ x ＜ 10$，所以当$x = \frac{20}{3}$时，$S_{\text{max}}=\frac{400}{3}\ \text{m}^2$。