《2025年暑期升级训练八年级数学浙教版浙江教育出版社》

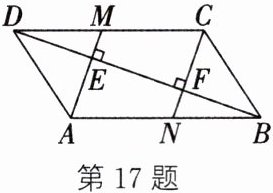
17. (12分)如图,在$□ ABCD$中,$BD$是它的一条对角线,过$A$,$C两点作AE⊥BD$,$CF⊥BD$,垂足分别为$E$,$F$,延长$AE$,$CF分别交CD$,$AB于点M$,$N$。
(1)求证：四边形$AMCN$是平行四边形；
(2)已知$DE= 2$,$FN= 1$,求$MD$的长。

答案：
(1)
∵四边形ABCD是平行四边形，
∴CD//AB。
∵AM⊥BD，CN⊥BD，
∴∠AED = ∠NFD = 90°。
∴AM//CN。又
∵CM//AN，
∴四边形AMCN是平行四边形。
(2)
∵四边形AMCN是平行四边形，
∴CM = AN。
∵四边形ABCD是平行四边形，
∴CD = AB，CD//AB。
∴MD = NB，∠MDE = ∠NBF。在△MDE和△NBF中，
∵$\begin{cases}\angle DEM = \angle BFN = 90^{\circ}\\\angle MDE = \angle NBF\\MD = NB\end{cases}$，
∴△MDE≌△NBF。
∴ME = NF = 1。在Rt△DME中，
∵∠DEM = 90°，DE = 2，ME = 1，
∴由勾股定理，得MD = $\sqrt{DE^{2}+ME^{2}}$ = $\sqrt{2^{2}+1^{2}}$ = $\sqrt{5}$

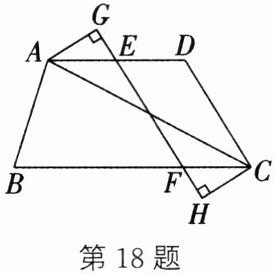
18. (12分)如图,在四边形$ABCD$中,$AD// BC$,点$E$,$F分别在边AD$,$BC$上,$AE= CF$,过点$A$,$C分别作EF$的垂线,垂足分别为$G$,$H$。
(1)求证：$\triangle AGE≌\triangle CHF$。
(2)连结$AC$,线段$GH与AC$是否互相平分？请说明理由。

答案：

(1)
∵AD//BC，
∴∠AEF = ∠CFE。
∴∠AEG = ∠CFH。
∵AG⊥EF，CH⊥EF，
∴∠AGE = ∠CHF = 90°。又
∵AE = CF，
∴△AGE≌△CHF。
(2)线段GH与AC互相平分。理由：如图，连结CG，AH。由
(1)，知△AGE≌△CHF，
∴AG = CH。
∵∠AGE = ∠CHF = 90°，
∴AG//CH。
∴四边形AHCG为平行四边形。
∴线段GH与AC互相平分。
　　　　　　　

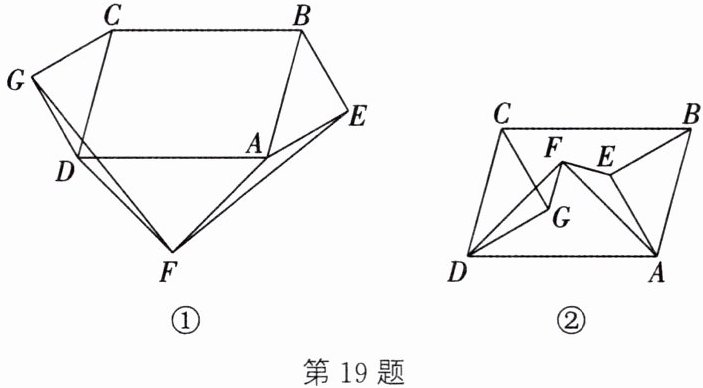
19. (12分)新考法 探究题 分别以$□ ABCD(∠CDA≠90^{\circ })的三边AB$,$CD$,$DA为斜边作等腰直角三角形ABE$、等腰直角三角形$CDG$、等腰直角三角形$ADF$。
(1)如图①,当三个等腰直角三角形都在该平行四边形的外部时,连结$GF$,$EF$。请判断$GF与EF$之间的关系,并进行证明。
(2)如图②,当三个等腰直角三角形都在该平行四边形的内部时,连结$GF$,$EF$,问题(1)中的结论还成立吗？若成立,请给出证明；若不成立,请说明理由。

答案：
(1)GF⊥EF，GF = EF。
∵四边形ABCD是平行四边形，
∴AB = CD，∠DAB + ∠ADC = 180°。
∵△ABE，△CDG，△ADF都是等腰直角三角形，
∴易得DG = CG = AE = BE，DF = AF，∠AFD = 90°，∠CDG = ∠ADF = ∠DAF = ∠BAE = 45°。
∴∠FDG = ∠CDG + ∠CDA + ∠ADF = 90° + ∠CDA，∠FAE = 360° - ∠BAE - ∠DAF - ∠BAD = 270° - (180° - ∠CDA) = 90° + ∠CDA。
∴∠FAE = ∠FDG。在△EAF和△GDF中，
∵$\begin{cases}AF = DF\\\angle FAE = \angle FDG\\AE = DG\end{cases}$，
∴△EAF≌△GDF。
∴EF = GF，∠EFA = ∠GFD。
∴∠GFD + ∠GFA = ∠EFA + ∠GFA，即∠AFD = ∠GFE = 90°。
∴GF⊥EF。
(2)问题
(1)中的结论还成立。
∵四边形ABCD是平行四边形，
∴AB = DC，∠DAB + ∠ADC = 180°。
∵△ABE，△CDG，△ADF都是等腰直角三角形，
∴∠DFA = 90°，DF = AF，∠CDG = ∠ADF = ∠DAF = ∠BAE = 45°，易得DG = AE。又
∵∠BAE + ∠DAF + ∠EAF + ∠ADF + ∠CDF = 180°，
∴∠EAF + ∠CDF = 45°。又
∵∠CDF + ∠GDF = 45°，
∴∠GDF = ∠EAF。
∴△GDF≌△EAF。
∴GF = EF，∠GFD = ∠EFA。
∴∠GFD + ∠GFA = ∠EFA + ∠GFA，即∠DFA = ∠GFE = 90°。
∴GF⊥EF。综上所述，问题
(1)中的结论还成立。