《2025年暑期升级训练八年级数学浙教版浙江教育出版社》

1. 有下列关于函数 $ y = 5 x ^ { 2 } $ 的图象和性质的说法：① 开口向上；② 对称轴是 $ y $ 轴；③ 顶点是坐标原点；④ 有最高点。其中,正确的有(C)
A.$ 1 $ 个
B.$ 2 $ 个
C.$ 3 $ 个
D.$ 4 $ 个

答案： 解：对于函数 $ y = 5x^2 $：
- ① 因为二次项系数 $ 5 ＞ 0 $，所以抛物线开口向上，正确；
- ② 对称轴为直线 $ x = 0 $，即 $ y $ 轴，正确；
- ③ 顶点坐标为 $ (0, 0) $，即坐标原点，正确；
- ④ 抛物线开口向上，有最低点，无最高点，错误。
综上，正确的有①②③，共3个。
答案：C

2. 若二次函数 $ y = a x ^ { 2 } $ 的图象经过点 $ P ( 2, 4 ) $,则该图象必经过点(B)
A.$ ( - 2, - 4 ) $
B.$ ( - 2, 4 ) $
C.$ ( - 4, 2 ) $
D.$ ( 4, - 2 ) $

答案： 解：将点$P(2,4)$代入$y = ax^2$，得$4 = a×2^2$，解得$a = 1$，所以二次函数解析式为$y = x^2$。
分别将选项代入：
- A. 当$x=-2$时，$y=(-2)^2=4\neq-4$，故不经过。
- B. 当$x=-2$时，$y=(-2)^2=4$，故经过。
- C. 当$x=-4$时，$y=(-4)^2=16\neq2$，故不经过。
- D. 当$x=4$时，$y=4^2=16\neq-2$，故不经过。
答案：B

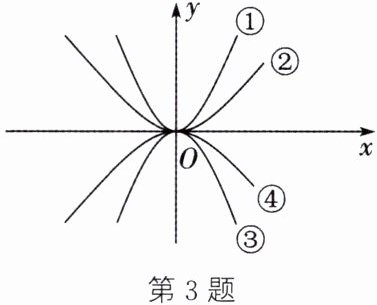
3. 如图所示的四个二次函数图象分别对应① $ y = a x ^ { 2 } $,② $ y = b x ^ { 2 } $,③ $ y = c x ^ { 2 } $,④ $ y = d x ^ { 2 } $,则 $ a $,$ b $,$ c $,$ d $ 的大小关系为$a ＞ b ＞ d ＞ c$(用“$ ＞ $”连接)。

答案： 解：对于二次函数$y = kx^2$，当$k＞0$时，抛物线开口向上；当$k＜0$时，抛物线开口向下。开口向上的抛物线中，$|k|$越大，开口越窄；开口向下的抛物线中，$|k|$越大，开口越窄。
观察图象可知，①②开口向上，所以$a＞0$，$b＞0$，且①比②开口窄，故$a ＞ b$；③④开口向下，所以$c＜0$，$d＜0$，且④比③开口窄，故$|d| ＞ |c|$，即$d ＞ c$。
综上，$a ＞ b ＞ d ＞ c$。
答案：$a ＞ b ＞ d ＞ c$

4. 已知点 $ A ( 3, 18 ) $ 与点 $ B ( - 1, k ) $ 都在二次函数 $ y = a x ^ { 2 } ( a \neq 0 ) $ 的图象上。
(1)求 $ a $ 和 $ k $ 的值；
(2)写出函数图象的对称轴、顶点坐标及开口方向；
(3)试判断这个函数的图象是否经过点 $ ( - 2, 10 ) $。

答案：
(1) 把 $ A(3, 18) $ 代入 $ y = ax^{2}(a \neq 0) $，得 $ 18 = a \cdot 3^{2} $，解得 $ a = 2 $。
$\therefore y = 2x^{2}$。
把 $ B(-1, k) $ 代入 $ y = 2x^{2} $，得 $ k = 2 × (-1)^{2} = 2 $。
(2) 函数 $ y = 2x^{2} $ 的对称轴是 y 轴，顶点坐标是 $ (0, 0) $，开口向上。
(3) 当 $ x = -2 $ 时，$ y = 2 × (-2)^{2} = 8 \neq 10 $，
$\therefore$ 这个函数的图象不经过点 $ (-2, 10) $。

5. 当 $ a b ＞ 0 $ 时,$ y = a x ^ { 2 } $ 与 $ y = a x + b $ 在平面直角坐标系中的图象大致是(D)

答案： 解：
1. 由 $ab ＞ 0$ 知 $a$，$b$ 同号。
2. 抛物线 $y = ax^2$：
若 $a ＞ 0$，开口向上；
若 $a ＜ 0$，开口向下。
3. 直线 $y = ax + b$：
当 $a ＞ 0$ 时，$b ＞ 0$，直线过第一、二、三象限；
当 $a ＜ 0$ 时，$b ＜ 0$，直线过第二、三、四象限。
4. 选项分析：
A：抛物线开口向上（$a ＞ 0$），直线过第一、三、四象限（$b ＜ 0$），$a$，$b$ 异号，不符合。
B：抛物线开口向上（$a ＞ 0$），直线过第一、二、四象限（$a ＜ 0$），矛盾，不符合。
C：抛物线开口向下（$a ＜ 0$），直线过第一、三、四象限（$a ＞ 0$），矛盾，不符合。
D：抛物线开口向下（$a ＜ 0$），直线过第二、三、四象限（$a ＜ 0$，$b ＜ 0$），符合。
答案：D

6. 已知二次函数 $ y = 2023 x ^ { 2 } $ 的图象经过原点,且其图象上有两个不同的点 $ P \left( t _ { 1 }, \frac { 1 } { 4 } \right) $,$ Q \left( t _ { 2 }, \frac { 1 } { 4 } \right) $,则 $ t _ { 1 } + t _ { 2 } = $0。

答案： 解：$∵$ 二次函数 $y = 2023x^2$ 的对称轴为 $y$ 轴，点 $P(t_1, \frac{1}{4})$，$Q(t_2, \frac{1}{4})$ 纵坐标相同且为不同点，
$∴$ 点 $P$ 与点 $Q$ 关于 $y$ 轴对称，
$∴ t_1 = -t_2$，
$∴ t_1 + t_2 = 0$。
0

7. 如图,二次函数 $ y = a x ^ { 2 } ( a \neq 0 ) $ 与一次函数 $ y = k x - 2 $ 的图象相交于 $ A ( - 1, - 1 ) $,$ B $ 两点,且直线 $ y = k x - 2 $ 交 $ y $ 轴于点 $ G $,求 $ \triangle O A B $ 的面积。

答案： 解：
∵一次函数$y=kx-2$的图象过点$A(-1,-1)$，
∴$-1=-k-2$，解得$k=-1$，
∴一次函数的表达式为$y=-x-2$。
令$x=0$，得$y=-2$，
∴点$G$的坐标为$(0,-2)$，$OG=2$。
∵二次函数$y=ax^2$的图象过点$A(-1,-1)$，
∴$-1=a×(-1)^2$，解得$a=-1$，
∴二次函数的表达式为$y=-x^2$。
联立$\begin{cases}y=-x-2\\y=-x^2\end{cases}$，
解得$\begin{cases}x_1=-1\\y_1=-1\end{cases}$，$\begin{cases}x_2=2\\y_2=-4\end{cases}$，
∴点$B$的坐标为$(2,-4)$。
$S_{\triangle OAB}=\frac{1}{2}OG\cdot|x_A|+\frac{1}{2}OG\cdot x_B=\frac{1}{2}×2×|-1|+\frac{1}{2}×2×2=1+2=3$。