第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
9. 新考向 传统文化(株洲中考)中药是以我国传统医药理论为指导,经过采集、炮制、制剂而得到的药物。在一个时间段,某中药房的黄芪、焦山楂、当归三种中药的销售价格和销售额情况如下表:
|中药|黄芪|焦山楂|当归|
|销售价格(元/千克)|80|60|90|
|销售额(元)|120|120|360|
在这个时间段,该中药房的这三种中药的平均销售量为______千克。
|中药|黄芪|焦山楂|当归|
|销售价格(元/千克)|80|60|90|
|销售额(元)|120|120|360|
在这个时间段,该中药房的这三种中药的平均销售量为______千克。
2.5
答案:
解:黄芪销售量:$120÷80 = 1.5$(千克)
焦山楂销售量:$120÷60 = 2$(千克)
当归销售量:$360÷90 = 4$(千克)
总销售量:$1.5 + 2 + 4 = 7.5$(千克)
平均销售量:$7.5÷3 = 2.5$(千克)
2.5
焦山楂销售量:$120÷60 = 2$(千克)
当归销售量:$360÷90 = 4$(千克)
总销售量:$1.5 + 2 + 4 = 7.5$(千克)
平均销售量:$7.5÷3 = 2.5$(千克)
2.5
10.(雅安中考)从$-1$,$\frac{1}{2}$,2中任取两个数相乘,所得乘积的中位数是
$-\frac{1}{2}$
。
答案:
从-1,$\frac{1}{2}$,2中任取两个数相乘,所有可能的乘积为:
-1×$\frac{1}{2}$=-$\frac{1}{2}$,
-1×2=-2,
$\frac{1}{2}$×2=1。
将乘积按从小到大排列为:-2,-$\frac{1}{2}$,1。
一共有3个数,中位数是第2个数,即-$\frac{1}{2}$。
$-\frac{1}{2}$
-1×$\frac{1}{2}$=-$\frac{1}{2}$,
-1×2=-2,
$\frac{1}{2}$×2=1。
将乘积按从小到大排列为:-2,-$\frac{1}{2}$,1。
一共有3个数,中位数是第2个数,即-$\frac{1}{2}$。
$-\frac{1}{2}$
11. 计算一组数据的方差时,列出的算式为$S^{2}= \frac{1}{10}[(x_{1}-8)^{2}+(x_{2}-8)^{2}+…+(x_{10}-8)^{2}]$。这组数据的个数为
10
,平均数为8
。
答案:
10 8
12. “红色小讲解员”演讲比赛中,7位评委分别给出某位选手一个原始评分。评定该选手成绩时,从7个原始评分中去掉1个最高分、1个最低分,得到5个有效评分。5个有效评分与7个原始评分相比,这两组数据一定不变的是______
中位数
(填“平均数”“中位数”或“众数”)。
答案:
中位数
13. $*$在按从小到大的顺序排列的五个数x,3,6,8,12中再加入一个数。若这六个数的中位数、平均数与原来五个数的中位数、平均数分别相等,则x的值为______。
1
答案:
解:原来五个数按从小到大排列为x,3,6,8,12,中位数是6。
加入一个数后变为六个数,中位数为中间两个数的平均数,要使中位数仍为6,则加入的数为6。
原来五个数的平均数为$\frac{x + 3 + 6 + 8 + 12}{5}$,六个数的平均数为$\frac{x + 3 + 6 + 6 + 8 + 12}{6}$。
由平均数相等可得方程:$\frac{x + 3 + 6 + 8 + 12}{5} = \frac{x + 3 + 6 + 6 + 8 + 12}{6}$
解得:$x = 1$
答案:1
加入一个数后变为六个数,中位数为中间两个数的平均数,要使中位数仍为6,则加入的数为6。
原来五个数的平均数为$\frac{x + 3 + 6 + 8 + 12}{5}$,六个数的平均数为$\frac{x + 3 + 6 + 6 + 8 + 12}{6}$。
由平均数相等可得方程:$\frac{x + 3 + 6 + 8 + 12}{5} = \frac{x + 3 + 6 + 6 + 8 + 12}{6}$
解得:$x = 1$
答案:1
14. 为了解当地气温变化情况,某研究小组记录了寒假期间连续6天的最高气温,结果如下(单位:℃):-6,-3,x,2,-1,3。若这组数据的中位数是-1,现给出下列结论:① 方差是8;② 众数是-1;③ 平均数是-1。其中,正确的是
②③
(填序号)。
答案:
解:
∵数据-6,-3,x,2,-1,3的中位数是-1,将数据排序后中间两个数的平均数为-1,
∴x=-1。
平均数:$\frac{-6 + (-3) + (-1) + 2 + (-1) + 3}{6} = \frac{-6 - 3 - 1 + 2 - 1 + 3}{6} = \frac{-6}{6} = -1$,故③正确。
方差:$\frac{1}{6}[(-6 + 1)^2 + (-3 + 1)^2 + (-1 + 1)^2 + (2 + 1)^2 + (-1 + 1)^2 + (3 + 1)^2]$
$= \frac{1}{6}[(-5)^2 + (-2)^2 + 0^2 + 3^2 + 0^2 + 4^2]$
$= \frac{1}{6}[25 + 4 + 0 + 9 + 0 + 16] = \frac{1}{6}×54 = 9$,故①错误。
众数:数据中-1出现2次,次数最多,故众数是-1,②正确。
正确的是②③。
∵数据-6,-3,x,2,-1,3的中位数是-1,将数据排序后中间两个数的平均数为-1,
∴x=-1。
平均数:$\frac{-6 + (-3) + (-1) + 2 + (-1) + 3}{6} = \frac{-6 - 3 - 1 + 2 - 1 + 3}{6} = \frac{-6}{6} = -1$,故③正确。
方差:$\frac{1}{6}[(-6 + 1)^2 + (-3 + 1)^2 + (-1 + 1)^2 + (2 + 1)^2 + (-1 + 1)^2 + (3 + 1)^2]$
$= \frac{1}{6}[(-5)^2 + (-2)^2 + 0^2 + 3^2 + 0^2 + 4^2]$
$= \frac{1}{6}[25 + 4 + 0 + 9 + 0 + 16] = \frac{1}{6}×54 = 9$,故①错误。
众数:数据中-1出现2次,次数最多,故众数是-1,②正确。
正确的是②③。
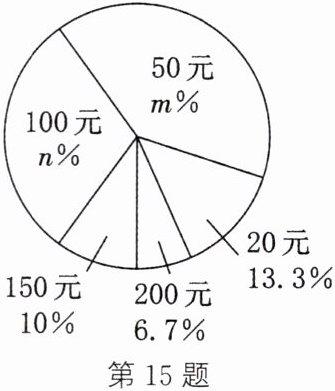
15.(12分)在一次爱心捐款活动中,某中学全体同学积极踊跃捐款。现抽查了九年级一班同学的捐款情况,并绘制出如下统计表和如图所示的统计图。
|捐款(元)|20|50|100|150|200|
|人数|4|12|9|3|2|
(1)m=
(2)求捐款数目的众数、中位数和平均数。
|捐款(元)|20|50|100|150|200|
|人数|4|12|9|3|2|
(1)m=
40
,n=30
;(2)求捐款数目的众数、中位数和平均数。

(2) ∵ 在这组数据中,“50”出现了12次,出现的次数最多,∴ 学生捐款数目的众数是50元.
∵ 将这组数据按照从小到大的顺序排列,处于中间位置的两个数据都是“50”,∴ 中位数为50元.
捐款数目的平均数为$(20×4 + 50×12 + 100×9 + 150×3 + 200×2)÷(4 + 12 + 9 + 3 + 2)=81$(元).
∵ 将这组数据按照从小到大的顺序排列,处于中间位置的两个数据都是“50”,∴ 中位数为50元.
捐款数目的平均数为$(20×4 + 50×12 + 100×9 + 150×3 + 200×2)÷(4 + 12 + 9 + 3 + 2)=81$(元).
答案:
(1) 40;30.
(2)
∵ 在这组数据中,“50”出现了12次,出现的次数最多,
∴ 学生捐款数目的众数是50元.
∵ 将这组数据按照从小到大的顺序排列,处于中间位置的两个数据都是“50”,
∴ 中位数为50元.
捐款数目的平均数为$(20×4 + 50×12 + 100×9 + 150×3 + 200×2)÷(4 + 12 + 9 + 3 + 2)=81$(元).
(1) 40;30.
(2)
∵ 在这组数据中,“50”出现了12次,出现的次数最多,
∴ 学生捐款数目的众数是50元.
∵ 将这组数据按照从小到大的顺序排列,处于中间位置的两个数据都是“50”,
∴ 中位数为50元.
捐款数目的平均数为$(20×4 + 50×12 + 100×9 + 150×3 + 200×2)÷(4 + 12 + 9 + 3 + 2)=81$(元).
16. $*$(12分)某公司销售部有营销人员15人,为了对达到或者超出月销售基础额的员工进行表彰,负责人统计了这15人某月的销售量记录在下表:
|销售量(件)|1400|880|270|150|130|120|
|人数|1|1|3|6|3|1|
(1)求该月这15人的销售量的平均数。
(2)假设销售部负责人把月销售基础额定为300件,合理吗?为什么?如果不合理,请你制定一个比较合理的月销售基础额,并说明理由。
|销售量(件)|1400|880|270|150|130|120|
|人数|1|1|3|6|3|1|
(1)求该月这15人的销售量的平均数。
(2)假设销售部负责人把月销售基础额定为300件,合理吗?为什么?如果不合理,请你制定一个比较合理的月销售基础额,并说明理由。
答案:
(1) 解:平均数 = $\frac{1}{15} × (1400 + 880 + 270 × 3 + 150 × 6 + 130 × 3 + 120)$
= $\frac{1}{15} × (1400 + 880 + 810 + 900 + 390 + 120)$
= $\frac{1}{15} × 4500$
= 300(件)
(2) 不合理。因为15人中有13人的月销售量不到300件,300件虽是平均数,但不能反映一般水平。
合理的月销售基础额为150件。理由:150件是中位数(第8位)和众数(出现6次),是大部分营销人员能达到的水平。
(1) 解:平均数 = $\frac{1}{15} × (1400 + 880 + 270 × 3 + 150 × 6 + 130 × 3 + 120)$
= $\frac{1}{15} × (1400 + 880 + 810 + 900 + 390 + 120)$
= $\frac{1}{15} × 4500$
= 300(件)
(2) 不合理。因为15人中有13人的月销售量不到300件,300件虽是平均数,但不能反映一般水平。
合理的月销售基础额为150件。理由:150件是中位数(第8位)和众数(出现6次),是大部分营销人员能达到的水平。
查看更多完整答案,请扫码查看


