第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
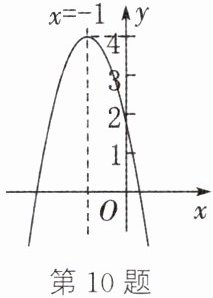
10. (齐齐哈尔中考)如图,抛物线 $ y = ax^{2} + bx + c $($ a \neq 0 $)与y轴的交点在点 $ (0, 1) $,$ (0, 2) $ 之间,对称轴为直线 $ x = - 1 $,函数的最大值为4,结合图象给出下列结论:① $ b = 2a $;② $ - 3 < a < - 2 $;③ $ 4ac - b^{2} < 0 $;④ 若关于x的一元二次方程 $ ax^{2} + bx + a = m - 4 $($ a \neq 0 $)有两个不相等的实数根,则 $ m > 4 $;⑤ 当 $ x < 0 $ 时,y随x的增大而减小. 其中,正确的有( )
A.2个
B.3个
C.4个
D.5个
B

A.2个
B.3个
C.4个
D.5个
答案:
B 解析:
∵抛物线的对称轴为直线x=-b/(2a)=-1,
∴b=2a。故①正确。
∵抛物线经过点(-1,4),
∴a-b+c=-a+c=4。
∴a=c-4。
∵抛物线与y轴的交点在点(0,1),(0,2)之间,
∴1<c<2。
∴-3<a<-2。故②正确。
∵抛物线与x轴有2个交点,
∴b²-4ac>0,即4ac-b²<0。故③正确。
∵a=c-4,
∴ax²+bx+a=m-4可整理为ax²+bx+c=m。
∵抛物线开口向下,顶点的坐标为(-1,4),
∴当m<4时,抛物线与直线y=m有两个不同的交点。故④错误。由图象,可得当x<-1时,y随x的增大而增大,故⑤错误。综上所述,正确的有3个。
∵抛物线的对称轴为直线x=-b/(2a)=-1,
∴b=2a。故①正确。
∵抛物线经过点(-1,4),
∴a-b+c=-a+c=4。
∴a=c-4。
∵抛物线与y轴的交点在点(0,1),(0,2)之间,
∴1<c<2。
∴-3<a<-2。故②正确。
∵抛物线与x轴有2个交点,
∴b²-4ac>0,即4ac-b²<0。故③正确。
∵a=c-4,
∴ax²+bx+a=m-4可整理为ax²+bx+c=m。
∵抛物线开口向下,顶点的坐标为(-1,4),
∴当m<4时,抛物线与直线y=m有两个不同的交点。故④错误。由图象,可得当x<-1时,y随x的增大而增大,故⑤错误。综上所述,正确的有3个。
11. 请你设计一个与y轴交于点 $ (0, 1) $,且当 $ x < 0 $ 时,y随x的增大而减小的抛物线对应的函数表达式:
$y = x^2 + 1$
.
答案:
解:设抛物线的函数表达式为 $ y = ax^2 + bx + c $。
因为抛物线与y轴交于点$(0,1)$,所以当$x=0$时,$y=1$,代入表达式可得$c = 1$。
抛物线的对称轴为$x = -\frac{b}{2a}$,当$x < 0$时,y随x的增大而减小,说明抛物线开口向上,即$a > 0$,且对称轴在y轴或y轴右侧,即$-\frac{b}{2a} \geq 0$。
取$a = 1$,$b = 0$,则函数表达式为$y = x^2 + 1$。
答案:$y = x^2 + 1$
因为抛物线与y轴交于点$(0,1)$,所以当$x=0$时,$y=1$,代入表达式可得$c = 1$。
抛物线的对称轴为$x = -\frac{b}{2a}$,当$x < 0$时,y随x的增大而减小,说明抛物线开口向上,即$a > 0$,且对称轴在y轴或y轴右侧,即$-\frac{b}{2a} \geq 0$。
取$a = 1$,$b = 0$,则函数表达式为$y = x^2 + 1$。
答案:$y = x^2 + 1$
12. 如图,在平面直角坐标系中,抛物线 $ y = ax^{2} + 3 $ 与y轴交于点A,过点A作与x轴平行的直线交抛物线 $ y = x^{2} $ 于点B,C,则BC的长为
$ 2\sqrt{3} $
.
答案:
解:对于抛物线 $ y = ax^2 + 3 $,令 $ x = 0 $,得 $ y = 3 $,所以点 $ A $ 的坐标为 $ (0, 3) $。
因为直线 $ BC $ 过点 $ A $ 且与 $ x $ 轴平行,所以直线 $ BC $ 的解析式为 $ y = 3 $。
联立 $ \begin{cases} y = 3 \\ y = x^2 \end{cases} $,得 $ x^2 = 3 $,解得 $ x = \sqrt{3} $ 或 $ x = -\sqrt{3} $。
所以点 $ B $ 的坐标为 $ (-\sqrt{3}, 3) $,点 $ C $ 的坐标为 $ (\sqrt{3}, 3) $。
则 $ BC = \sqrt{3} - (-\sqrt{3}) = 2\sqrt{3} $。
答案:$ 2\sqrt{3} $
因为直线 $ BC $ 过点 $ A $ 且与 $ x $ 轴平行,所以直线 $ BC $ 的解析式为 $ y = 3 $。
联立 $ \begin{cases} y = 3 \\ y = x^2 \end{cases} $,得 $ x^2 = 3 $,解得 $ x = \sqrt{3} $ 或 $ x = -\sqrt{3} $。
所以点 $ B $ 的坐标为 $ (-\sqrt{3}, 3) $,点 $ C $ 的坐标为 $ (\sqrt{3}, 3) $。
则 $ BC = \sqrt{3} - (-\sqrt{3}) = 2\sqrt{3} $。
答案:$ 2\sqrt{3} $
13. 若点 $ P(a, b) $ 在抛物线 $ y = - 2x^{2} + 2x + 1 $ 上,则 $ a - b $ 的最小值为______
$-\frac{9}{8}$
.
答案:
解:因为点$P(a,b)$在抛物线$y = -2x^{2} + 2x + 1$上,所以$b=-2a^{2}+2a + 1$。
则$a - b=a-(-2a^{2}+2a + 1)=2a^{2}-a - 1$。
对于二次函数$y=2a^{2}-a - 1$,其中$A=2$,$B=-1$,$C=-1$。
因为$A=2>0$,所以函数有最小值,当$a=-\frac{B}{2A}=-\frac{-1}{2×2}=\frac{1}{4}$时,
$a - b$的最小值为$2×(\frac{1}{4})^{2}-\frac{1}{4}-1=2×\frac{1}{16}-\frac{1}{4}-1=\frac{1}{8}-\frac{2}{8}-\frac{8}{8}=-\frac{9}{8}$。
$-\frac{9}{8}$
则$a - b=a-(-2a^{2}+2a + 1)=2a^{2}-a - 1$。
对于二次函数$y=2a^{2}-a - 1$,其中$A=2$,$B=-1$,$C=-1$。
因为$A=2>0$,所以函数有最小值,当$a=-\frac{B}{2A}=-\frac{-1}{2×2}=\frac{1}{4}$时,
$a - b$的最小值为$2×(\frac{1}{4})^{2}-\frac{1}{4}-1=2×\frac{1}{16}-\frac{1}{4}-1=\frac{1}{8}-\frac{2}{8}-\frac{8}{8}=-\frac{9}{8}$。
$-\frac{9}{8}$
14. 如果将抛物线 $ y = x^{2} + 2x - 1 $ 向上平移,使它经过点 $ A(0, 3) $,那么所得的新抛物线对应的函数表达式为______
$y = x^{2} + 2x + 3$
.
答案:
解:设平移后的抛物线表达式为$y = x^{2} + 2x - 1 + k$($k>0$)。
因为新抛物线经过点$A(0, 3)$,将$x=0$,$y=3$代入表达式得:
$3 = 0^{2} + 2×0 - 1 + k$
$3 = -1 + k$
解得$k = 4$
所以新抛物线对应的函数表达式为$y = x^{2} + 2x - 1 + 4 = x^{2} + 2x + 3$
答案:$y = x^{2} + 2x + 3$
因为新抛物线经过点$A(0, 3)$,将$x=0$,$y=3$代入表达式得:
$3 = 0^{2} + 2×0 - 1 + k$
$3 = -1 + k$
解得$k = 4$
所以新抛物线对应的函数表达式为$y = x^{2} + 2x - 1 + 4 = x^{2} + 2x + 3$
答案:$y = x^{2} + 2x + 3$
15. 已知二次函数 $ y = - (x - 2)^{2} + c $,当 $ x = x_{1} $ 时,函数值为 $ y_{1} $;当 $ x = x_{2} $ 时,函数值为 $ y_{2} $. 若 $ |x_{1} - 2| > |x_{2} - 2| $,则 $ y_{1} $,$ y_{2} $ 的大小关系是______(用“<”连接).
y₁<y₂
答案:
解:
∵二次函数$y=-(x - 2)^2 + c$,
∴抛物线开口向下,对称轴为直线$x=2$,
∵$|x_{1} - 2|>|x_{2} - 2|$,
∴点$(x_{1}, y_{1})$到对称轴的距离大于点$(x_{2}, y_{2})$到对称轴的距离,
又
∵抛物线开口向下,
∴$y_{1}<y_{2}$。
$y_{1}<y_{2}$
∵二次函数$y=-(x - 2)^2 + c$,
∴抛物线开口向下,对称轴为直线$x=2$,
∵$|x_{1} - 2|>|x_{2} - 2|$,
∴点$(x_{1}, y_{1})$到对称轴的距离大于点$(x_{2}, y_{2})$到对称轴的距离,
又
∵抛物线开口向下,
∴$y_{1}<y_{2}$。
$y_{1}<y_{2}$
16. 如图,在四边形ABCD中,E,F,G,H分别是边AB,BC,CD,AD的中点. 若四边形EFGH是矩形,且其周长是20,则四边形ABCD的面积最大是______.
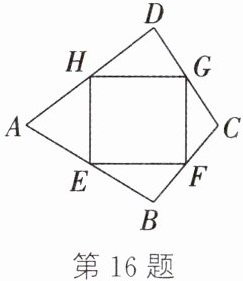

答案:
解:连结AC,BD交于点O。
∵E,F,G,H分别是边AB,BC,CD,AD的中点,
∴根据三角形中位线性质,得2EF=AC,2EH=BD,EF//AC//HG,EH//BD//GF。
∵四边形EFGH是矩形,
∴EF⊥EH,
∴AC⊥BD,
∴四边形ABCD的面积=$\frac{1}{2}$BD·AC。
设EH=x,则BD=2x,
∵四边形EFGH周长为20,
∴EF=10-x,AC=2(10-x),
∴面积S=$\frac{1}{2}×2x×2(10-x)=-2x^2+20x=-2(x-5)^2+50$。
∵-2<0,0<x<10,
∴当x=5时,S最大=50。
50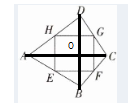
解:连结AC,BD交于点O。
∵E,F,G,H分别是边AB,BC,CD,AD的中点,
∴根据三角形中位线性质,得2EF=AC,2EH=BD,EF//AC//HG,EH//BD//GF。
∵四边形EFGH是矩形,
∴EF⊥EH,
∴AC⊥BD,
∴四边形ABCD的面积=$\frac{1}{2}$BD·AC。
设EH=x,则BD=2x,
∵四边形EFGH周长为20,
∴EF=10-x,AC=2(10-x),
∴面积S=$\frac{1}{2}×2x×2(10-x)=-2x^2+20x=-2(x-5)^2+50$。
∵-2<0,0<x<10,
∴当x=5时,S最大=50。
50

17. (10分)已知抛物线 $ y = 2x^{2} - 4x + c $ 与x轴有两个不同的交点.
(1)求c的取值范围;
(2)若抛物线 $ y = 2x^{2} - 4x + c $ 经过点 $ A(2, m) $ 和 $ B(3, n) $,试比较m与n的大小,并说明理由.
(1)求c的取值范围;
(2)若抛物线 $ y = 2x^{2} - 4x + c $ 经过点 $ A(2, m) $ 和 $ B(3, n) $,试比较m与n的大小,并说明理由.
答案:
(1)解:
∵抛物线$y = 2x^{2}-4x + c$与$x$轴有两个不同的交点,
∴方程$2x^{2}-4x + c = 0$的判别式$\Delta>0$。
$\Delta=(-4)^{2}-4×2c = 16 - 8c$,
∴$16-8c>0$,解得$c<2$。
(2)$m < n$。理由:抛物线$y = 2x^{2}-4x + c$的对称轴为直线$x=-\frac{-4}{2×2}=1$。
∵$2>0$,
∴抛物线开口向上,当$x\geq1$时,$y$随$x$的增大而增大。
∵点$A(2,m)$和$B(3,n)$都在对称轴$x = 1$的右侧,且$2<3$,
∴$m < n$。
(1)解:
∵抛物线$y = 2x^{2}-4x + c$与$x$轴有两个不同的交点,
∴方程$2x^{2}-4x + c = 0$的判别式$\Delta>0$。
$\Delta=(-4)^{2}-4×2c = 16 - 8c$,
∴$16-8c>0$,解得$c<2$。
(2)$m < n$。理由:抛物线$y = 2x^{2}-4x + c$的对称轴为直线$x=-\frac{-4}{2×2}=1$。
∵$2>0$,
∴抛物线开口向上,当$x\geq1$时,$y$随$x$的增大而增大。
∵点$A(2,m)$和$B(3,n)$都在对称轴$x = 1$的右侧,且$2<3$,
∴$m < n$。
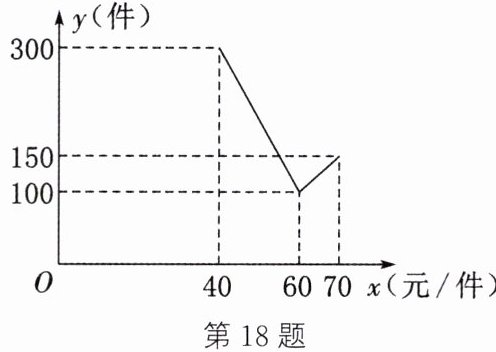
18. (12分)(营口中考)某商家正在销售一种商品,其成本为30元/件,在销售过程中发现,随着售价的增加,销售量在减少. 当售价为60元/件时,商家决定改变销售策略,此时售价每增加1元/件,需支付由此产生的额外费用为150元. 该商品的销售量 $ y(件) $ 与售价 $ x(元/件) $ 满足如图所示的函数关系(其中 $ 40 \leq x \leq 70 $,且x为整数).
(1)求y关于x的函数表达式.
(2)当售价为多少时,该商家获得的利润最大?最大利润是多少?
(1)求y关于x的函数表达式.
(2)当售价为多少时,该商家获得的利润最大?最大利润是多少?

答案:
(1)当$40 \leq x \leq 60$时,设$y = kx + b(k \neq 0)$。把$(40, 300)$,$(60, 100)$代入,得$\begin{cases}300 = 40k + b \\ 100 = 60k + b\end{cases}$,解得$\begin{cases}k = -10 \\ b = 700\end{cases}$,$\therefore y = -10x + 700$。
当$60 < x \leq 70$时,设$y = mx + n(m \neq 0)$。把$(60, 100)$,$(70, 150)$代入,得$\begin{cases}100 = 60m + n \\ 150 = 70m + n\end{cases}$,解得$\begin{cases}m = 5 \\ n = -200\end{cases}$,$\therefore y = 5x - 200$。
综上所述,$y$关于$x$的函数表达式为$y = \begin{cases}-10x + 700(40 \leq x \leq 60) \\ 5x - 200(60 < x \leq 70)\end{cases}$。
(2)设商家获得的利润为$w$元。
当$40 \leq x \leq 60$时,$w = (x - 30)(-10x + 700) = -10(x - 50)^2 + 4000$。
$\because -10 < 0$,$\therefore$当$x = 50$时,$w$取到最大值$4000$。
当$60 < x \leq 70$时,$w = (x - 30)(5x - 200) - 150(x - 60) = 5(x - 50)^2 + 2500$。
$\because 5 > 0$,$\therefore$当$60 < x \leq 70$时,$w$随$x$的增大而增大。
$\therefore$当$x = 70$时,$w$取到最大值,此时$w = 5×(70 - 50)^2 + 2500 = 4500$。
$\because 4000 < 4500$,$\therefore$当售价为$70$元/件时,该商家获得的利润最大,最大利润是$4500$元。
(1)当$40 \leq x \leq 60$时,设$y = kx + b(k \neq 0)$。把$(40, 300)$,$(60, 100)$代入,得$\begin{cases}300 = 40k + b \\ 100 = 60k + b\end{cases}$,解得$\begin{cases}k = -10 \\ b = 700\end{cases}$,$\therefore y = -10x + 700$。
当$60 < x \leq 70$时,设$y = mx + n(m \neq 0)$。把$(60, 100)$,$(70, 150)$代入,得$\begin{cases}100 = 60m + n \\ 150 = 70m + n\end{cases}$,解得$\begin{cases}m = 5 \\ n = -200\end{cases}$,$\therefore y = 5x - 200$。
综上所述,$y$关于$x$的函数表达式为$y = \begin{cases}-10x + 700(40 \leq x \leq 60) \\ 5x - 200(60 < x \leq 70)\end{cases}$。
(2)设商家获得的利润为$w$元。
当$40 \leq x \leq 60$时,$w = (x - 30)(-10x + 700) = -10(x - 50)^2 + 4000$。
$\because -10 < 0$,$\therefore$当$x = 50$时,$w$取到最大值$4000$。
当$60 < x \leq 70$时,$w = (x - 30)(5x - 200) - 150(x - 60) = 5(x - 50)^2 + 2500$。
$\because 5 > 0$,$\therefore$当$60 < x \leq 70$时,$w$随$x$的增大而增大。
$\therefore$当$x = 70$时,$w$取到最大值,此时$w = 5×(70 - 50)^2 + 2500 = 4500$。
$\because 4000 < 4500$,$\therefore$当售价为$70$元/件时,该商家获得的利润最大,最大利润是$4500$元。
查看更多完整答案,请扫码查看


