第21页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
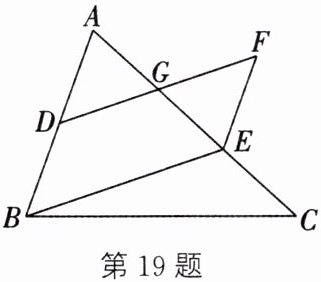
19. (5 分)如图,在$\triangle ABC$中,D 为 AB 的中点,点 E 在 AC 上,$BE// DF$,$BE= DF$,DF 交 AC 于点 G,连结 EF. 求证:$AG= EG$.

答案:
如图, 连结 DE,AF.
∵ $BE// DF$, $BE = DF$,
∴ 四边形 DBEF 是平行四边形.
∴ $BD// EF$, $BD = EF$.
∴ $AD// EF$.
∵ D 为 AB 的中点,
∴ $AD = BD$.
∴ $AD = EF$.
∴ 四边形 ADEF 是平行四边形.
∴ $AG = EG$.

如图, 连结 DE,AF.
∵ $BE// DF$, $BE = DF$,
∴ 四边形 DBEF 是平行四边形.
∴ $BD// EF$, $BD = EF$.
∴ $AD// EF$.
∵ D 为 AB 的中点,
∴ $AD = BD$.
∴ $AD = EF$.
∴ 四边形 ADEF 是平行四边形.
∴ $AG = EG$.

20. (8 分)据统计,某小区居民 2020 年年底家庭轿车的保有量为 81 辆,2022 年年底家庭轿车的保有量达到 144 辆.
(1)若该小区居民 2020 年年底到 2023 年年底家庭轿车保有量的年增长率都相同,则该小区居民到 2023 年年底家庭轿车的保有量将达到多少辆?
(2)小区物业决定将向业主出租 100 个地下停车位,通过调查发现:当每个停车位的月租金为 300 元时,可以出租 50 个停车位;当每个停车位的月租金每降低 10 元时,可以多出租 5 个停车位. 若物业计划停车位的月租金收入为 19 200 元,则应将每个停车位的月租金定为多少元?
(1)若该小区居民 2020 年年底到 2023 年年底家庭轿车保有量的年增长率都相同,则该小区居民到 2023 年年底家庭轿车的保有量将达到多少辆?
(2)小区物业决定将向业主出租 100 个地下停车位,通过调查发现:当每个停车位的月租金为 300 元时,可以出租 50 个停车位;当每个停车位的月租金每降低 10 元时,可以多出租 5 个停车位. 若物业计划停车位的月租金收入为 19 200 元,则应将每个停车位的月租金定为多少元?
答案:
(1) 设家庭轿车保有量的年增长率为$x$。由题意,得$81(1 + x)^{2}=144$,解得$x_{1}=\frac{1}{3}$,$x_{2}=-\frac{7}{3}$(不合题意,舍去)。$\therefore 144×(1+\frac{1}{3}) = 192$(辆)。答:该小区居民到2023年年底家庭轿车的保有量将达到192辆。
(2) 设应将每个停车位的月租金定为$y$元,则可出租$50 + 5×\frac{300 - y}{10}=(200-\frac{y}{2})$个停车位。由题意,得$y(200-\frac{y}{2})=19200$。整理,得$y^{2}-400y + 38400 = 0$,解得$y_{1}=160$,$y_{2}=240$。当$y = 160$时,$200-\frac{y}{2}=120>100$,不合题意,舍去;当$y = 240$时,$200-\frac{y}{2}=80<100$,符合题意。答:应将每个停车位的月租金定为240元。
(1) 设家庭轿车保有量的年增长率为$x$。由题意,得$81(1 + x)^{2}=144$,解得$x_{1}=\frac{1}{3}$,$x_{2}=-\frac{7}{3}$(不合题意,舍去)。$\therefore 144×(1+\frac{1}{3}) = 192$(辆)。答:该小区居民到2023年年底家庭轿车的保有量将达到192辆。
(2) 设应将每个停车位的月租金定为$y$元,则可出租$50 + 5×\frac{300 - y}{10}=(200-\frac{y}{2})$个停车位。由题意,得$y(200-\frac{y}{2})=19200$。整理,得$y^{2}-400y + 38400 = 0$,解得$y_{1}=160$,$y_{2}=240$。当$y = 160$时,$200-\frac{y}{2}=120>100$,不合题意,舍去;当$y = 240$时,$200-\frac{y}{2}=80<100$,符合题意。答:应将每个停车位的月租金定为240元。
21. (8 分)某校举办了一次知识竞赛,本次竞赛的满分为 10 分,学生的得分均为整数,成绩达到 6 分及 6 分以上为合格,达到 9 分或 10 分为优秀. 在这次竞赛中,甲、乙两组学生的成绩分布折线统计图如图所示,成绩统计分析表如下:
|组 别|平均数(分)|中位数(分)|方差(分^2)|合格率|优秀率|
|甲组|6.8|a|3.76|90%|30%|
|乙组|b|7.5|1.96|80%|20%|
解答下列问题:
(1)$a=$
(2)小敏说:“这次竞赛我得了 7 分,在我们小组中排名属中游略偏上.”观察表格后思考判断,小敏是
(3)甲组学生认为他们组的合格率、优秀率均高于乙组,因此他们组的成绩比乙组好. 但乙组学生不同意甲组学生的观点,认为他们的成绩要好于甲组. 请你写出两条支持乙组学生的观点的理由.
|组 别|平均数(分)|中位数(分)|方差(分^2)|合格率|优秀率|
|甲组|6.8|a|3.76|90%|30%|
|乙组|b|7.5|1.96|80%|20%|
解答下列问题:
(1)$a=$
6
;$b=$7.2
.(2)小敏说:“这次竞赛我得了 7 分,在我们小组中排名属中游略偏上.”观察表格后思考判断,小敏是
甲
(填“甲”或“乙”)组的学生.(3)甲组学生认为他们组的合格率、优秀率均高于乙组,因此他们组的成绩比乙组好. 但乙组学生不同意甲组学生的观点,认为他们的成绩要好于甲组. 请你写出两条支持乙组学生的观点的理由.
①乙组的平均分高于甲组,总体平均水平高. ②乙组的方差比甲组小,成绩更稳定.
答案:
(1) 6;7.2.
(2) 甲.
(3) ①乙组的平均分高于甲组,总体平均水平高. ②乙组的方差比甲组小,成绩更稳定.
(1) 6;7.2.
(2) 甲.
(3) ①乙组的平均分高于甲组,总体平均水平高. ②乙组的方差比甲组小,成绩更稳定.
查看更多完整答案,请扫码查看


