第40页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
12. 如图,在正方形ABCD中,对角线AC,BD相交于点O,点E在DO上,DE= 2EO,连结AE。将△ADE沿AD翻折,得△ADE',F是AE的中点,连结E'F。若DE= 2$\sqrt{2}$,求△AFE'的面积。


答案:
解:连结EE',交AD于点G。
由翻折性质,得EE'⊥AD,E'G=EG,∠DGE=90°。
∵四边形ABCD是正方形,
∴∠ADE=45°,△DGE是等腰直角三角形。
∵DE=2$\sqrt{2}$,
∴EG=DG=2(等腰直角三角形直角边=斜边/$\sqrt{2}$)。
∴E'G=2,EE'=EG+E'G=4。
∵DE=2EO,DE=2$\sqrt{2}$,
∴EO=$\sqrt{2}$,DO=DE+EO=3$\sqrt{2}$。
∵四边形ABCD是正方形,
∴AO=DO=3$\sqrt{2}$,AC⊥BD,∠AOD=90°。
在Rt△ADO中,AD=$\sqrt{AO^2+DO^2}$=$\sqrt{(3\sqrt{2})^2+(3\sqrt{2})^2}$=6。
∴AG=AD-DG=6-2=4。
△AEE'的面积=$\frac{1}{2}$×EE'×AG=$\frac{1}{2}$×4×4=8。
∵F是AE中点,
∴△AFE'的面积=$\frac{1}{2}$△AEE'的面积=4。
答:△AFE'的面积为4。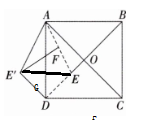
解:连结EE',交AD于点G。
由翻折性质,得EE'⊥AD,E'G=EG,∠DGE=90°。
∵四边形ABCD是正方形,
∴∠ADE=45°,△DGE是等腰直角三角形。
∵DE=2$\sqrt{2}$,
∴EG=DG=2(等腰直角三角形直角边=斜边/$\sqrt{2}$)。
∴E'G=2,EE'=EG+E'G=4。
∵DE=2EO,DE=2$\sqrt{2}$,
∴EO=$\sqrt{2}$,DO=DE+EO=3$\sqrt{2}$。
∵四边形ABCD是正方形,
∴AO=DO=3$\sqrt{2}$,AC⊥BD,∠AOD=90°。
在Rt△ADO中,AD=$\sqrt{AO^2+DO^2}$=$\sqrt{(3\sqrt{2})^2+(3\sqrt{2})^2}$=6。
∴AG=AD-DG=6-2=4。
△AEE'的面积=$\frac{1}{2}$×EE'×AG=$\frac{1}{2}$×4×4=8。
∵F是AE中点,
∴△AFE'的面积=$\frac{1}{2}$△AEE'的面积=4。
答:△AFE'的面积为4。

13. 小明尝试着将矩形纸片ABCD(AD>CD)先沿过点A的直线折叠,使得点B落在边AD上的点F处,折痕为AE(如图①);再沿过点D的直线折叠,使得点C落在边DA上的点N处,点E落在边AE上的点M处,折痕为DG(如图②)。如果第二次折叠后,点M正好在∠NDG的平分线DM上,求矩形ABCD的长边长与短边长的比值。


答案:
解:连结DE。
∵沿过点A的直线折叠,点B落在边AD上的点F处,
∴∠EAD=45°。
∵第二次折叠后,点M在∠NDG的平分线上,
∴DE平分∠CDG,即∠GDE=∠CDE。
∵DG为折痕,
∴∠DGE=∠DGA=90°。
∵四边形ABCD是矩形,
∴∠C=90°,
∴∠DGE=∠C。
又
∵DE=DE,
∴△DGE≌△DCE(AAS),
∴DG=DC。
∵∠EAD=45°,∠DGA=90°,
∴△AGD为等腰直角三角形,
∴AD=$\sqrt{2}$DG。
∵DG=DC,
∴AD=$\sqrt{2}$DC,
即AD:DC=$\sqrt{2}$。
答:矩形ABCD的长边长与短边长的比值为$\sqrt{2}$。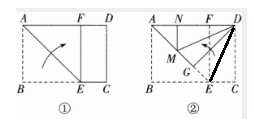
解:连结DE。
∵沿过点A的直线折叠,点B落在边AD上的点F处,
∴∠EAD=45°。
∵第二次折叠后,点M在∠NDG的平分线上,
∴DE平分∠CDG,即∠GDE=∠CDE。
∵DG为折痕,
∴∠DGE=∠DGA=90°。
∵四边形ABCD是矩形,
∴∠C=90°,
∴∠DGE=∠C。
又
∵DE=DE,
∴△DGE≌△DCE(AAS),
∴DG=DC。
∵∠EAD=45°,∠DGA=90°,
∴△AGD为等腰直角三角形,
∴AD=$\sqrt{2}$DG。
∵DG=DC,
∴AD=$\sqrt{2}$DC,
即AD:DC=$\sqrt{2}$。
答:矩形ABCD的长边长与短边长的比值为$\sqrt{2}$。

14. 如图,正方形ABCD的边长为4,P为边AD上的一点(不与点A,D重合)。将正方形ABCD折叠,使点B落在点P处,点C落在点G处,PG交DC于点H,折痕为EF,延长BC,PG相交于点K,连结BP,BH。
(1)若BE= 3,求AP的长。
(2)在(1)的条件下,求BK的长。
(3)当点P在边AD上移动时,△PDH的周长是定值吗?如果是,请求出该定值;如果不是,请说明理由。

(1)若BE= 3,求AP的长。
(2)在(1)的条件下,求BK的长。
(3)当点P在边AD上移动时,△PDH的周长是定值吗?如果是,请求出该定值;如果不是,请说明理由。

答案:
(1) 由折叠,可知 $ PE = BE = 3 $。
∵ $ AE = AB - BE $,$ AB = 4 $,
∴ $ AE = 1 $。
∵ 四边形 $ ABCD $ 是正方形,
∴ $ \angle A = 90^\circ $。
在 $ \text{Rt}\triangle AEP $ 中,由勾股定理,得
$ AP = \sqrt{EP^2 - AE^2} = \sqrt{3^2 - 1^2} = 2\sqrt{2} $。
(2) 过点 $ P $ 作 $ PN \perp BC $ 于点 $ N $,则 $ \angle PNB = 90^\circ $。
∵ 四边形 $ ABCD $ 是正方形,
∴ $ \angle A = \angle ABC = 90^\circ $,
∴ 四边形 $ ABNP $ 是矩形,
∴ $ AP = BN = 2\sqrt{2} $,$ AB = PN = 4 $。
由折叠,可知 $ \angle EPK = \angle ABC = 90^\circ $,$ EP = BE $,
∴ $ \angle EPB = \angle EBP $,
∴ $ \angle EPK - \angle EPB = \angle ABC - \angle EBP $,即 $ \angle BPK = \angle PBK $,
∴ $ BK = PK $。
在 $ \text{Rt}\triangle PNK $ 中,$ NK = BK - BN = BK - 2\sqrt{2} $,
由勾股定理,得 $ PK^2 = PN^2 + NK^2 $,
∴ $ BK^2 = 4^2 + (BK - 2\sqrt{2})^2 $,解得 $ BK = 3\sqrt{2} $。
(3) 是定值。
过点 $ B $ 作 $ BM \perp PG $ 于点 $ M $。
∵ 四边形 $ ABCD $ 是正方形,
∴ $ AD // BC $,$ AB = BC $,
∴ $ \angle APB = \angle PBK $,又 $ \angle BPK = \angle PBK $,
∴ $ \angle APB = \angle BPK $。
∵ $ \angle A = \angle BMP = 90^\circ $,$ BP = BP $,
∴ $ \triangle ABP \cong \triangle MBP $,
∴ $ AP = MP $,$ AB = MB $,
∵ $ AB = BC $,
∴ $ BM = BC $。
在 $ \text{Rt}\triangle BCH $ 和 $ \text{Rt}\triangle BMH $ 中,
$ \begin{cases} BH = BH \\ BC = BM \end{cases} $,
∴ $ \text{Rt}\triangle BCH \cong \text{Rt}\triangle BMH $,
∴ $ CH = MH $。
∴ $ \triangle PDH $ 的周长 $ = PD + PH + DH = PD + PM + MH + DH = PD + AP + CH + DH = AD + CD = 4 + 4 = 8 $。
故 $ \triangle PDH $ 的周长为定值 8。
(1) 由折叠,可知 $ PE = BE = 3 $。
∵ $ AE = AB - BE $,$ AB = 4 $,
∴ $ AE = 1 $。
∵ 四边形 $ ABCD $ 是正方形,
∴ $ \angle A = 90^\circ $。
在 $ \text{Rt}\triangle AEP $ 中,由勾股定理,得
$ AP = \sqrt{EP^2 - AE^2} = \sqrt{3^2 - 1^2} = 2\sqrt{2} $。
(2) 过点 $ P $ 作 $ PN \perp BC $ 于点 $ N $,则 $ \angle PNB = 90^\circ $。
∵ 四边形 $ ABCD $ 是正方形,
∴ $ \angle A = \angle ABC = 90^\circ $,
∴ 四边形 $ ABNP $ 是矩形,
∴ $ AP = BN = 2\sqrt{2} $,$ AB = PN = 4 $。
由折叠,可知 $ \angle EPK = \angle ABC = 90^\circ $,$ EP = BE $,
∴ $ \angle EPB = \angle EBP $,
∴ $ \angle EPK - \angle EPB = \angle ABC - \angle EBP $,即 $ \angle BPK = \angle PBK $,
∴ $ BK = PK $。
在 $ \text{Rt}\triangle PNK $ 中,$ NK = BK - BN = BK - 2\sqrt{2} $,
由勾股定理,得 $ PK^2 = PN^2 + NK^2 $,
∴ $ BK^2 = 4^2 + (BK - 2\sqrt{2})^2 $,解得 $ BK = 3\sqrt{2} $。
(3) 是定值。
过点 $ B $ 作 $ BM \perp PG $ 于点 $ M $。
∵ 四边形 $ ABCD $ 是正方形,
∴ $ AD // BC $,$ AB = BC $,
∴ $ \angle APB = \angle PBK $,又 $ \angle BPK = \angle PBK $,
∴ $ \angle APB = \angle BPK $。
∵ $ \angle A = \angle BMP = 90^\circ $,$ BP = BP $,
∴ $ \triangle ABP \cong \triangle MBP $,
∴ $ AP = MP $,$ AB = MB $,
∵ $ AB = BC $,
∴ $ BM = BC $。
在 $ \text{Rt}\triangle BCH $ 和 $ \text{Rt}\triangle BMH $ 中,
$ \begin{cases} BH = BH \\ BC = BM \end{cases} $,
∴ $ \text{Rt}\triangle BCH \cong \text{Rt}\triangle BMH $,
∴ $ CH = MH $。
∴ $ \triangle PDH $ 的周长 $ = PD + PH + DH = PD + PM + MH + DH = PD + AP + CH + DH = AD + CD = 4 + 4 = 8 $。
故 $ \triangle PDH $ 的周长为定值 8。
查看更多完整答案,请扫码查看


