《2025年暑期升级训练八年级数学浙教版浙江教育出版社》

1. 如图,将边长为13的菱形ABCD沿AD方向平移至四边形DCEF的位置,作EG⊥AB,交BA的延长线于点G,连结GD并延长,交EF于点H,连结BD。已知BD= 24,则GH= 20。

答案： 解：连结AC，DE，AC交BD于点O。
∵四边形ABCD和四边形DCEF是菱形，BD=24，
∴OA=OC，OB=OD=$\frac{1}{2}$BD=12，AC⊥BD，AB//CD//EF，AB=AD=CD=FD=13，AD//CE。
∴OA=$\sqrt {(AB²-OB²)}=\sqrt {(13²-12²)}$=5，四边形ACED是平行四边形。
∴DE=AC=2OA=10。
在△ADG和△FDH中，
∵∠ADG=∠FDH，AD=FD，∠GAD=∠F，
∴△ADG≌△FDH（ASA）。
∴DG=DH。
∵EG⊥AB，AB//EF，
∴∠BGE=∠GEF=90°。
∴DE=DG=DH（直角三角形斜边中线等于斜边一半）。
∴GH=2DE=20。
答案：20

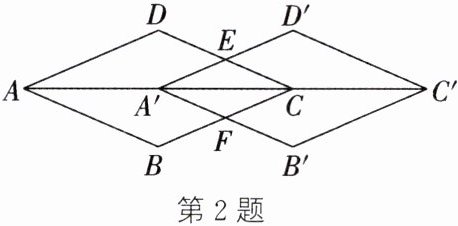
2. 如图,将菱形ABCD沿AC方向平移至四边形A'B'C'D'的位置,A'D'交CD于点E,A'B'交BC于点F,判断四边形A'FCE是不是菱形,并说明理由。

答案： 四边形A'FCE是菱形。理由如下：
∵四边形ABCD是菱形，
∴AD=CD，AD//BC，AB//CD，
∴∠DAC=∠DCA。
∵菱形ABCD沿AC方向平移至四边形A'B'C'D'的位置，
∴AD//A'D'，DC//D'C'，
∴∠DAC=∠D'A'C，A'E//BC，CE//A'B'，
∴四边形A'FCE是平行四边形。
∵∠D'A'C=∠DCA，
∴EA'=EC，
∴四边形A'FCE是菱形。

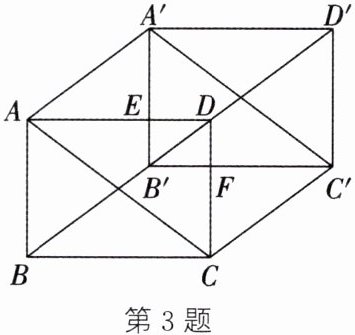
3. 新考法 探究题 如图,在矩形ABCD中,AB= 6cm,BC= 8cm,连结BD,将矩形ABCD沿BD方向平移得到矩形A'B'C'D',设BB'= x cm。依次连结A'A,AC,CC',C'A',四边形ACC'A'可能是菱形吗？若可能是,求出x的值；若不可能是,请说明理由。

答案： 四边形ACC'A'可能是菱形。
解：
∵四边形ABCD是矩形，
∴∠ABC=90°。
在Rt△ABC中，AB=6cm，BC=8cm，
由勾股定理，得AC²=AB²+BC²=6²+8²=36+64=100(cm²)，
∴AC=10cm。
∵矩形ABCD沿BD方向平移得到矩形A'B'C'D'，
∴AA'//CC'，AA'=CC'，
∴四边形ACC'A'是平行四边形。
若四边形ACC'A'是菱形，则AA'=AC=10cm。
∵平移距离BB'=x cm，且AA'=BB'，
∴x=10。
即x的值为10。

4. 如图,把菱形ABCD沿AH折叠,点B落在边BC上的点E处。若∠BAE= 40°,则∠EDC的度数为(B)
A.10°
B.15°
C.18°
D.20°

答案： 解：
∵ 四边形ABCD是菱形，
∴ AB=BC=CD=AD，∠B=∠ADC，AD//BC。
由折叠性质得：AB=AE，∠BAH=∠EAH。
∵ ∠BAE=40°，
∴ ∠BAH=∠EAH=20°，△ABE中，AB=AE，
∴ ∠B=∠AEB=(180°-40°)/2=70°，
∴ ∠ADC=∠B=70°。
∵ AD//BC，
∴ ∠DAE=∠AEB=70°（两直线平行，内错角相等），
∴ △ADE中，AD=AE，∠DAE=70°，
∴ ∠ADE=(180°-70°)/2=55°，
∴ ∠EDC=∠ADC-∠ADE=70°-55°=15°。
答案：B

5. 如图,在正方形纸片ABCD中,M,N分别是AD,BC的中点,连结MN,把BC向上翻折,使点C恰好落在MN上的点P处,BQ为折痕,则∠PBQ的度数为(C)
A.15°
B.20°
C.30°
D.45°

答案： C