第13页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
1. 如图,延长矩形ABCD的边BC至点E,使CE= BD,连结AE.若∠ADB= 40°,则∠E的度数是(

A.20°
B.25°
C.30°
D.35°
A
)
A.20°
B.25°
C.30°
D.35°
答案:
解:
∵四边形ABCD是矩形,
∴AD//BC,AC=BD,∠ADB=∠CAD=40°(矩形对角线相等且互相平分,内错角相等)。
∵CE=BD,
∴CE=AC,
∴∠E=∠CAE(等腰三角形两底角相等)。
∵AD//BC,
∴∠E=∠DAE(内错角相等)。
∵∠CAD=∠CAE+∠DAE=2∠E=40°,
∴∠E=20°。
答案:A
∵四边形ABCD是矩形,
∴AD//BC,AC=BD,∠ADB=∠CAD=40°(矩形对角线相等且互相平分,内错角相等)。
∵CE=BD,
∴CE=AC,
∴∠E=∠CAE(等腰三角形两底角相等)。
∵AD//BC,
∴∠E=∠DAE(内错角相等)。
∵∠CAD=∠CAE+∠DAE=2∠E=40°,
∴∠E=20°。
答案:A
2. (河池中考)如图,在菱形ABCD中,对角线AC,BD相交于点O.下列结论中,错误的是(
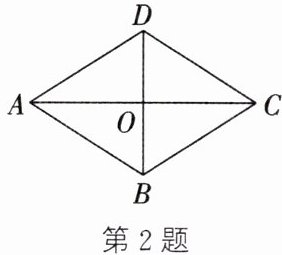
A.AB= AD
B.AC⊥BD
C.AC= BD
D.∠DAC= ∠BAC
C
)
A.AB= AD
B.AC⊥BD
C.AC= BD
D.∠DAC= ∠BAC
答案:
解:菱形的性质:
- 菱形的四条边相等,所以AB=AD,A正确;
- 菱形的对角线互相垂直,所以AC⊥BD,B正确;
- 菱形的对角线不一定相等,只有正方形(特殊菱形)对角线才相等,C错误;
- 菱形的对角线平分一组对角,所以∠DAC=∠BAC,D正确。
结论:错误的是C。
C
- 菱形的四条边相等,所以AB=AD,A正确;
- 菱形的对角线互相垂直,所以AC⊥BD,B正确;
- 菱形的对角线不一定相等,只有正方形(特殊菱形)对角线才相等,C错误;
- 菱形的对角线平分一组对角,所以∠DAC=∠BAC,D正确。
结论:错误的是C。
C
3. 如图,四边形ABCD为平行四边形,延长AD到点E,使DE= AD,连结EB,EC,DB.若添加一个条件,不能使四边形DBCE成为矩形,则该条件可以是(
A.AB= BE
B.CE⊥DE
C.∠ADB= 90°
D.BE⊥DC
D
)A.AB= BE
B.CE⊥DE
C.∠ADB= 90°
D.BE⊥DC
答案:
解:
∵四边形ABCD是平行四边形,
∴AD=BC,AD//BC,
∵DE=AD,
∴DE=BC,DE//BC,
∴四边形DBCE是平行四边形.
A.
∵AB=BE,AB=CD,
∴BE=CD,
∴平行四边形DBCE是矩形;
B.
∵CE⊥DE,∠E=90°,
∴平行四边形DBCE是矩形;
C.
∵∠ADB=90°,
∴∠EDB=90°,
∴平行四边形DBCE是矩形;
D. BE⊥DC,平行四边形DBCE是菱形,不一定是矩形.
答案:D
∵四边形ABCD是平行四边形,
∴AD=BC,AD//BC,
∵DE=AD,
∴DE=BC,DE//BC,
∴四边形DBCE是平行四边形.
A.
∵AB=BE,AB=CD,
∴BE=CD,
∴平行四边形DBCE是矩形;
B.
∵CE⊥DE,∠E=90°,
∴平行四边形DBCE是矩形;
C.
∵∠ADB=90°,
∴∠EDB=90°,
∴平行四边形DBCE是矩形;
D. BE⊥DC,平行四边形DBCE是菱形,不一定是矩形.
答案:D
4. 如图,四边形ABCD是菱形,AC与BD相交于点O.若AC= 8,DB= 6,DH⊥AB于点H,则DH的长为(
A.$\frac{12}{5}$
B.$\frac{24}{5}$
C.5
D.$\frac{27}{5}$
B
)A.$\frac{12}{5}$
B.$\frac{24}{5}$
C.5
D.$\frac{27}{5}$
答案:
解:
∵四边形ABCD是菱形,AC=8,DB=6,
∴AC⊥BD,OA=OC=4,OB=OD=3。
在Rt△AOB中,AB=$\sqrt{OA^2+OB^2}=\sqrt{4^2+3^2}=5$。
菱形ABCD面积=$\frac{1}{2}×AC×BD=\frac{1}{2}×8×6=24$。
又
∵菱形ABCD面积=AB×DH,
∴5×DH=24,解得DH=$\frac{24}{5}$。
答案:B
∵四边形ABCD是菱形,AC=8,DB=6,
∴AC⊥BD,OA=OC=4,OB=OD=3。
在Rt△AOB中,AB=$\sqrt{OA^2+OB^2}=\sqrt{4^2+3^2}=5$。
菱形ABCD面积=$\frac{1}{2}×AC×BD=\frac{1}{2}×8×6=24$。
又
∵菱形ABCD面积=AB×DH,
∴5×DH=24,解得DH=$\frac{24}{5}$。
答案:B
5. 如图,四边形ABCD是平行四边形,以点A为圆心、AB的长为半径画弧交AD于点F,再分别以点B,F为圆心、大于$\frac{1}{2}BF$的长为半径画弧,两弧在BC下方交于点M,作射线AM交BC于点E,连结EF.下列结论中,不一定成立的是(
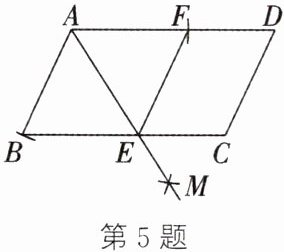
A.BE= EF
B.EF//CD
C.EA平分∠BEF
D.AB= EA
D
)
A.BE= EF
B.EF//CD
C.EA平分∠BEF
D.AB= EA
答案:
解:
∵四边形ABCD是平行四边形,
∴AD//BC,AB=CD,∠DAE=∠AEB。
由作图知,AF=AB,AM平分∠BAF,
∴∠BAE=∠FAE。
∵∠DAE=∠AEB,∠FAE=∠DAE,
∴∠FAE=∠AEB,
∴EF=AF=AB。
∵AB=AF,∠BAE=∠FAE,AE=AE,
∴△ABE≌△AFE(SAS),
∴BE=EF,∠AEB=∠AEF,即EA平分∠BEF。
∵EF=AB=CD,AD//BC,
∴四边形CDEF是平行四边形(或证∠BEF=∠C,得EF//CD)。
综上,A、B、C成立,D不一定成立。
答案:D
∵四边形ABCD是平行四边形,
∴AD//BC,AB=CD,∠DAE=∠AEB。
由作图知,AF=AB,AM平分∠BAF,
∴∠BAE=∠FAE。
∵∠DAE=∠AEB,∠FAE=∠DAE,
∴∠FAE=∠AEB,
∴EF=AF=AB。
∵AB=AF,∠BAE=∠FAE,AE=AE,
∴△ABE≌△AFE(SAS),
∴BE=EF,∠AEB=∠AEF,即EA平分∠BEF。
∵EF=AB=CD,AD//BC,
∴四边形CDEF是平行四边形(或证∠BEF=∠C,得EF//CD)。
综上,A、B、C成立,D不一定成立。
答案:D
6. 如图,矩形ABCD的对角线AC,BD交于点O,AB= 3,BC= 4,过点O作OM⊥AC,交BC于点M,过点M作MN⊥BD,垂足为N,则OM+MN的值为(
A.$\frac{24}{5}$
B.$\frac{16}{5}$
C.$\frac{12}{5}$
D.$\frac{6}{5}$
C
)A.$\frac{24}{5}$
B.$\frac{16}{5}$
C.$\frac{12}{5}$
D.$\frac{6}{5}$
答案:
C 解析:由勾股定理,易得 $ AC = 5 $,再根据矩形的对角线相等且互相平分,可知 $ BO = CO = \frac{1}{2}AC = \frac{5}{2} $。根据 $ S_{\triangle BOC} = S_{\triangle BOM} + S_{\triangle MOC} $,且 $ S_{\triangle BOC} = \frac{1}{2} × 3 × 4 × \frac{1}{2} = 3 $,可得 $ \frac{1}{2}BO \cdot MN + \frac{1}{2}CO \cdot OM = 3 $,从而可得 $ OM + MN = \frac{12}{5} $。
7. 如图,在正方形ABCD中,M,N为CD,BC上的点,且DM= CN,AM与DN交于点P,连结AN,Q为AN的中点,连结PQ.若AB= 10,DM= 4,则PQ的长为(
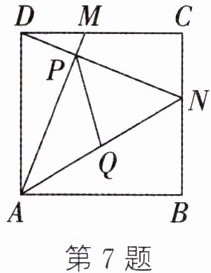
A.$4\sqrt{5}$
B.$8\sqrt{2}$
C.$\sqrt{34}$
D.$\frac{16\sqrt{5}}{3}$
C
)
A.$4\sqrt{5}$
B.$8\sqrt{2}$
C.$\sqrt{34}$
D.$\frac{16\sqrt{5}}{3}$
答案:
C 解析:
∵ 四边形 $ ABCD $ 是正方形,
∴ $ AD = DC = BC = AB = 10 $,$ \angle ADC = \angle C = \angle B = 90^{\circ} $。又
∵ $ DM = CN $,
∴ $ \triangle ADM \cong \triangle DCN $。
∴ $ \angle DAM = \angle CDN $。
∴ $ \angle APN = \angle DAM + \angle ADP = \angle CDN + \angle ADP = \angle ADC = 90^{\circ} $,即 $ \triangle ANP $ 为直角三角形。
∵ $ CN = DM = 4 $,$ BC = 10 $,
∴ $ BN = 6 $。在 $ Rt\triangle ABN $ 中,由勾股定理,得 $ AN = \sqrt{AB^{2} + BN^{2}} = 2\sqrt{34} $。再由直角三角形斜边上的中线等于斜边的一半,得 $ PQ = \frac{1}{2}AN = \sqrt{34} $。
∵ 四边形 $ ABCD $ 是正方形,
∴ $ AD = DC = BC = AB = 10 $,$ \angle ADC = \angle C = \angle B = 90^{\circ} $。又
∵ $ DM = CN $,
∴ $ \triangle ADM \cong \triangle DCN $。
∴ $ \angle DAM = \angle CDN $。
∴ $ \angle APN = \angle DAM + \angle ADP = \angle CDN + \angle ADP = \angle ADC = 90^{\circ} $,即 $ \triangle ANP $ 为直角三角形。
∵ $ CN = DM = 4 $,$ BC = 10 $,
∴ $ BN = 6 $。在 $ Rt\triangle ABN $ 中,由勾股定理,得 $ AN = \sqrt{AB^{2} + BN^{2}} = 2\sqrt{34} $。再由直角三角形斜边上的中线等于斜边的一半,得 $ PQ = \frac{1}{2}AN = \sqrt{34} $。
8. 如图,在Rt△ABC中,∠BAC= 90°,D,E分别是边AB,AC上的点,连结DE,DC,BE,分别取DE,BE,BC,DC的中点F,G,H,I,并依次连结四点得四边形FGHI,且四边形FGHI是正方形,需满足的条件是(
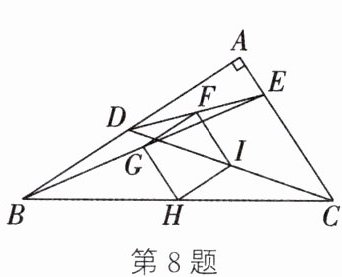
A.DC= BE
B.DC⊥BE
C.BD= CE
D.AB= AC
C
)
A.DC= BE
B.DC⊥BE
C.BD= CE
D.AB= AC
答案:
C 解析:当 $ BD = CE $ 时,四边形 $ FGHI $ 是正方形。
∵ $ F $,$ G $,$ H $,$ I $ 分别是 $ DE $,$ BE $,$ BC $,$ DC $ 的中点,
∴ $ FG // BD $,$ FG = \frac{1}{2}BD $,$ IH // BD $,$ IH = \frac{1}{2}BD $。
∴ $ FG // IH $,$ FG = IH $。
∴ 四边形 $ FGHI $ 是平行四边形。同理,可得 $ FI // CE $,$ FI = \frac{1}{2}CE $,
∴ $ \angle FID = \angle ACD $。
∵ $ BD // IH $,
∴ $ \angle ADC = \angle DIH $。
∵ $ \angle BAC = 90^{\circ} $,
∴ $ \angle ADC + \angle ACD = 90^{\circ} $。
∴ $ \angle DIH + \angle FID = 90^{\circ} $,即 $ \angle FIH = 90^{\circ} $。
∴ 四边形 $ FGHI $ 是矩形。
∵ $ BD = CE $,
∴ $ FG = FI $。
∴ 四边形 $ FGHI $ 是正方形。
∵ $ F $,$ G $,$ H $,$ I $ 分别是 $ DE $,$ BE $,$ BC $,$ DC $ 的中点,
∴ $ FG // BD $,$ FG = \frac{1}{2}BD $,$ IH // BD $,$ IH = \frac{1}{2}BD $。
∴ $ FG // IH $,$ FG = IH $。
∴ 四边形 $ FGHI $ 是平行四边形。同理,可得 $ FI // CE $,$ FI = \frac{1}{2}CE $,
∴ $ \angle FID = \angle ACD $。
∵ $ BD // IH $,
∴ $ \angle ADC = \angle DIH $。
∵ $ \angle BAC = 90^{\circ} $,
∴ $ \angle ADC + \angle ACD = 90^{\circ} $。
∴ $ \angle DIH + \angle FID = 90^{\circ} $,即 $ \angle FIH = 90^{\circ} $。
∴ 四边形 $ FGHI $ 是矩形。
∵ $ BD = CE $,
∴ $ FG = FI $。
∴ 四边形 $ FGHI $ 是正方形。
查看更多完整答案,请扫码查看


