第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
1. 二次函数 $ y = ax^{2}+bx + c(a\neq0) $ 的图象是一条
2. 对于生活中的抛物线形的实际问题,建立平面直角坐标系可确定其图象上几个关键点的坐标,运用
抛物线
,它的对称轴是直线$x=-\dfrac{b}{2a}$
,顶点坐标是$\left(-\dfrac{b}{2a},\dfrac{4ac-b^{2}}{4a}\right)$
。当 $ a > 0 $ 时,抛物线的开口向上
,顶点是抛物线上的最低
点;当 $ a < 0 $ 时,抛物线的开口向下
,顶点是抛物线上的最高
点。2. 对于生活中的抛物线形的实际问题,建立平面直角坐标系可确定其图象上几个关键点的坐标,运用
待定系数法
可求出抛物线对应的函数表达式,由此解决实际问题。
答案:
1. 抛物线;$x=-\dfrac{b}{2a}$;$\left(-\dfrac{b}{2a},\dfrac{4ac-b^{2}}{4a}\right)$;上;低;下;高
2. 待定系数法
2. 待定系数法
典例 1
已知二次函数 $ y = x^{2}-4x + 3 $。
(1) 用配方法将 $ y = x^{2}-4x + 3 $ 化成 $ y = a(x - h)^{2}+k $ 的形式;
(2) 写出该二次函数的图象的对称轴与顶点坐标;
(3) 在如图所示的平面直角坐标系中,画出这个二次函数的图象。
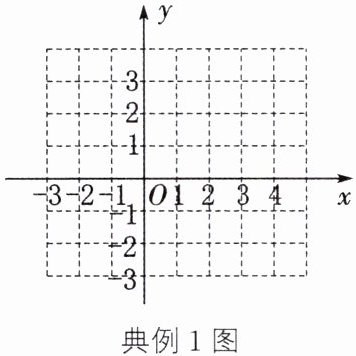
点拨 通过配方将二次函数的一般式化为顶点式,然后写出图象的对称轴和顶点坐标;画二次函数的图象时,可以采用“五点法”描点、连线画出。
解答:
解有所悟:用“五点法”画二次函数的图象时通常在下面的点中取“五点”:(1) 二次函数图象的顶点;(2) 二次函数图象与坐标轴 ($ x $ 轴、$ y $ 轴) 的交点;(3) 从二次函数图象上任取一点,任取一个 $ x $ 的值代入函数表达式求出 $ y $ 的值。将上述五点在平面直角坐标系中画出,然后用光滑的曲线顺次连结即可。
已知二次函数 $ y = x^{2}-4x + 3 $。
(1) 用配方法将 $ y = x^{2}-4x + 3 $ 化成 $ y = a(x - h)^{2}+k $ 的形式;
(2) 写出该二次函数的图象的对称轴与顶点坐标;
(3) 在如图所示的平面直角坐标系中,画出这个二次函数的图象。

点拨 通过配方将二次函数的一般式化为顶点式,然后写出图象的对称轴和顶点坐标;画二次函数的图象时,可以采用“五点法”描点、连线画出。
解答:
解有所悟:用“五点法”画二次函数的图象时通常在下面的点中取“五点”:(1) 二次函数图象的顶点;(2) 二次函数图象与坐标轴 ($ x $ 轴、$ y $ 轴) 的交点;(3) 从二次函数图象上任取一点,任取一个 $ x $ 的值代入函数表达式求出 $ y $ 的值。将上述五点在平面直角坐标系中画出,然后用光滑的曲线顺次连结即可。
答案:
(1) 配方,得 $ y = (x - 2)^2 - 1 $。
(2) 对称轴为直线 $ x = 2 $,顶点坐标为 $ (2, -1) $。
(3) 取二次函数图象上的五个特殊点:$ (0, 3) $,$ (1, 0) $,$ (2, -1) $,$ (3, 0) $,$ (4, 3) $,将上述五点描出,并用光滑的曲线顺次连结,得到如图所示的函数图象。

(1) 配方,得 $ y = (x - 2)^2 - 1 $。
(2) 对称轴为直线 $ x = 2 $,顶点坐标为 $ (2, -1) $。
(3) 取二次函数图象上的五个特殊点:$ (0, 3) $,$ (1, 0) $,$ (2, -1) $,$ (3, 0) $,$ (4, 3) $,将上述五点描出,并用光滑的曲线顺次连结,得到如图所示的函数图象。

典例 2
已知抛物线 $ y = ax^{2}-ax(a\neq0) $ 经过点 $ (-1,2) $。
(1) 求该抛物线对应的函数表达式和顶点坐标。
(2) 能否通过平移上面的抛物线得到抛物线 $ y = x^{2}+3x+\frac{1}{2} $?如果能,请说明平移方式;如果不能,请说明理由。
点拨 (1) 利用待定系数法将 $ (-1,2) $ 代入函数表达式求出 $ a $ 的值,然后通过配方将表达式转化为顶点式,写出顶点坐标。(2) 分别求出两抛物线的顶点坐标,根据抛物线顶点坐标的变化规律解答。
解答:
解有所悟:解决这类问题的关键是确定平移前、后抛物线的顶点坐标,再由平移规律得到所求的平移方式。
已知抛物线 $ y = ax^{2}-ax(a\neq0) $ 经过点 $ (-1,2) $。
(1) 求该抛物线对应的函数表达式和顶点坐标。
(2) 能否通过平移上面的抛物线得到抛物线 $ y = x^{2}+3x+\frac{1}{2} $?如果能,请说明平移方式;如果不能,请说明理由。
点拨 (1) 利用待定系数法将 $ (-1,2) $ 代入函数表达式求出 $ a $ 的值,然后通过配方将表达式转化为顶点式,写出顶点坐标。(2) 分别求出两抛物线的顶点坐标,根据抛物线顶点坐标的变化规律解答。
解答:
解有所悟:解决这类问题的关键是确定平移前、后抛物线的顶点坐标,再由平移规律得到所求的平移方式。
答案:
(1) 把点$(-1, 2)$代入$y = ax^2 - ax(a \neq 0)$,得$a(-1)^2 - a(-1) = 2$,即$a + a = 2$,解得$a = 1$。所以该抛物线对应的函数表达式为$y = x^2 - x$。
$\because y = x^2 - x = x^2 - x + \frac{1}{4} - \frac{1}{4} = \left(x - \frac{1}{2}\right)^2 - \frac{1}{4}$,$\therefore$顶点坐标为$\left(\frac{1}{2}, -\frac{1}{4}\right)$。
(2) 能。
$\because y = x^2 + 3x + \frac{1}{2} = x^2 + 3x + \frac{9}{4} - \frac{9}{4} + \frac{1}{2} = \left(x + \frac{3}{2}\right)^2 - \frac{7}{4}$,$\therefore$平移后抛物线的顶点坐标是$\left(-\frac{3}{2}, -\frac{7}{4}\right)$。
原抛物线顶点坐标为$\left(\frac{1}{2}, -\frac{1}{4}\right)$,顶点横坐标变化:$-\frac{3}{2} - \frac{1}{2} = -2$,即向左平移2个单位;顶点纵坐标变化:$-\frac{7}{4} - \left(-\frac{1}{4}\right) = -\frac{6}{4} = -\frac{3}{2}$,即向下平移$\frac{3}{2}$个单位。
所以将抛物线$y = x^2 - x$先向左平移2个单位,再向下平移$\frac{3}{2}$个单位可得到抛物线$y = x^2 + 3x + \frac{1}{2}$。
(1) 把点$(-1, 2)$代入$y = ax^2 - ax(a \neq 0)$,得$a(-1)^2 - a(-1) = 2$,即$a + a = 2$,解得$a = 1$。所以该抛物线对应的函数表达式为$y = x^2 - x$。
$\because y = x^2 - x = x^2 - x + \frac{1}{4} - \frac{1}{4} = \left(x - \frac{1}{2}\right)^2 - \frac{1}{4}$,$\therefore$顶点坐标为$\left(\frac{1}{2}, -\frac{1}{4}\right)$。
(2) 能。
$\because y = x^2 + 3x + \frac{1}{2} = x^2 + 3x + \frac{9}{4} - \frac{9}{4} + \frac{1}{2} = \left(x + \frac{3}{2}\right)^2 - \frac{7}{4}$,$\therefore$平移后抛物线的顶点坐标是$\left(-\frac{3}{2}, -\frac{7}{4}\right)$。
原抛物线顶点坐标为$\left(\frac{1}{2}, -\frac{1}{4}\right)$,顶点横坐标变化:$-\frac{3}{2} - \frac{1}{2} = -2$,即向左平移2个单位;顶点纵坐标变化:$-\frac{7}{4} - \left(-\frac{1}{4}\right) = -\frac{6}{4} = -\frac{3}{2}$,即向下平移$\frac{3}{2}$个单位。
所以将抛物线$y = x^2 - x$先向左平移2个单位,再向下平移$\frac{3}{2}$个单位可得到抛物线$y = x^2 + 3x + \frac{1}{2}$。
查看更多完整答案,请扫码查看


