第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
10. (怀化中考)已知点$A(-2,b)与点B(a,3)$关于原点对称,则$a-b= $
5
。
答案:
解:因为点$A(-2,b)$与点$B(a,3)$关于原点对称,所以两点的横、纵坐标均互为相反数。
则$a = -(-2) = 2$,$b = -3$。
所以$a - b = 2 - (-3) = 5$。
5
则$a = -(-2) = 2$,$b = -3$。
所以$a - b = 2 - (-3) = 5$。
5
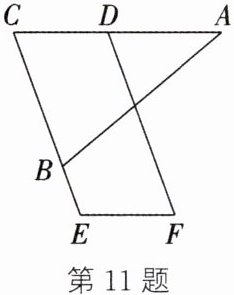
11. 如图,在$\triangle ABC$中,$AB= AC$,延长$CB至点E$,点$D在边AC$上,以$CE$,$CD为边作□ DCEF$。若$∠F= 70^{\circ }$,则$∠A$的度数为______$^{\circ }$。

40
答案:
解:
∵四边形DCEF是平行四边形,
∴∠C=∠F=70°。
∵AB=AC,
∴∠ABC=∠C=70°。
在△ABC中,∠A=180°-∠ABC-∠C=180°-70°-70°=40°。
40
∵四边形DCEF是平行四边形,
∴∠C=∠F=70°。
∵AB=AC,
∴∠ABC=∠C=70°。
在△ABC中,∠A=180°-∠ABC-∠C=180°-70°-70°=40°。
40
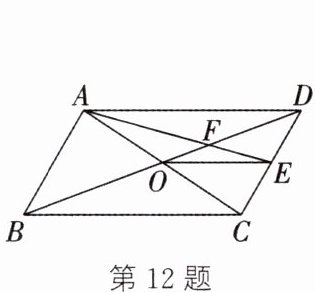
12. 如图,$O是□ ABCD的对角线AC$,$BD$的交点,$E为CD$的中点,$AE交BD于点F$,连结$OE$。若$S_{\triangle AOE}= 3$,则$S_{\triangle AOB}= $______。

6
答案:
解:
∵四边形ABCD是平行四边形,
∴O是AC中点。
∵E为CD中点,
∴OE是△ACD的中位线,
∴OE//AD,OE = $\frac{1}{2}$AD。
∵OE//AD,
∴△AOE与△AOD等高,且OE : AD = 1 : 2,
∴$S_{\triangle AOE} : S_{\triangle AOD} = 1 : 2$。
∵$S_{\triangle AOE} = 3$,
∴$S_{\triangle AOD} = 6$。
∵O是平行四边形ABCD对角线交点,
∴$S_{\triangle AOB} = S_{\triangle AOD} = 6$。
6
∵四边形ABCD是平行四边形,
∴O是AC中点。
∵E为CD中点,
∴OE是△ACD的中位线,
∴OE//AD,OE = $\frac{1}{2}$AD。
∵OE//AD,
∴△AOE与△AOD等高,且OE : AD = 1 : 2,
∴$S_{\triangle AOE} : S_{\triangle AOD} = 1 : 2$。
∵$S_{\triangle AOE} = 3$,
∴$S_{\triangle AOD} = 6$。
∵O是平行四边形ABCD对角线交点,
∴$S_{\triangle AOB} = S_{\triangle AOD} = 6$。
6
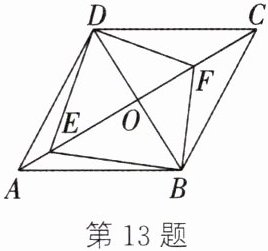
13. 如图,在$□ ABCD$中,对角线$AC$,$BD相交于点O$,$BD= 12cm$,$AC= 20cm$。现点$E从点A$出发,以$1cm/s的速度向点C$运动,同时点$F从点C$出发,以$2cm/s的速度向点A$运动。在点$E与点F$相遇前,四边形$DEBF$______(填“会”或“不会”)成为平行四边形。

不会
答案:
解:
∵四边形ABCD是平行四边形
∴OA=OC,OB=OD
设运动时间为t秒(t>0),则AE=t cm,CF=2t cm
∵AC=20cm
∴OE=OA - AE=10 - t,OF=OC - CF=10 - 2t
若四边形DEBF为平行四边形,则OE=OF
即10 - t=10 - 2t,解得t=0
∵点E与点F在相遇前运动,t>0
∴OE≠OF
∴四边形DEBF不会成为平行四边形
不会
∵四边形ABCD是平行四边形
∴OA=OC,OB=OD
设运动时间为t秒(t>0),则AE=t cm,CF=2t cm
∵AC=20cm
∴OE=OA - AE=10 - t,OF=OC - CF=10 - 2t
若四边形DEBF为平行四边形,则OE=OF
即10 - t=10 - 2t,解得t=0
∵点E与点F在相遇前运动,t>0
∴OE≠OF
∴四边形DEBF不会成为平行四边形
不会
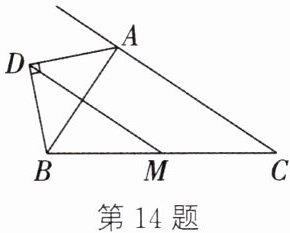
14. 如图,在$\triangle ABC$中,$M为BC$的中点,$AD为\triangle ABC$的外角平分线,且$AD⊥BD$,连结$MD$。若$AB= 6$,$AC= 9$,则$MD$的长为______。

答案:
解:延长BD交CA的延长线于点E。
∵AD为△ABC的外角平分线,
∴∠EAD=∠BAD。
∵AD⊥BD,
∴∠ADE=∠ADB=90°。
在△ADE和△ADB中,
$\left\{\begin{array}{l} ∠EAD=∠BAD\\ AD=AD\\ ∠ADE=∠ADB\end{array}\right.$
∴△ADE≌△ADB(ASA)。
∴DE=DB,AE=AB=6。
∴CE=AC+AE=9+6=15。
∵M为BC的中点,D为BE的中点,
∴MD是△BCE的中位线。
∴MD=$\frac{1}{2}$CE=$\frac{1}{2}$×15=7.5。
7.5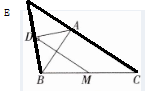
解:延长BD交CA的延长线于点E。
∵AD为△ABC的外角平分线,
∴∠EAD=∠BAD。
∵AD⊥BD,
∴∠ADE=∠ADB=90°。
在△ADE和△ADB中,
$\left\{\begin{array}{l} ∠EAD=∠BAD\\ AD=AD\\ ∠ADE=∠ADB\end{array}\right.$
∴△ADE≌△ADB(ASA)。
∴DE=DB,AE=AB=6。
∴CE=AC+AE=9+6=15。
∵M为BC的中点,D为BE的中点,
∴MD是△BCE的中位线。
∴MD=$\frac{1}{2}$CE=$\frac{1}{2}$×15=7.5。
7.5

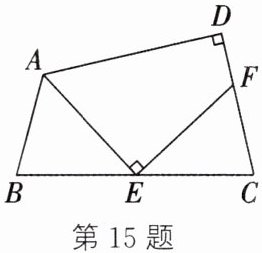
15. (8分)如图,在四边形$ABCD$中,$∠D= 90^{\circ }$,$E是边BC$上一点,连结$AE$,$EF⊥AE$,交$CD于点F$。
(1)若$∠EAD= 60^{\circ }$,求$∠DFE$的度数;
(2)若$∠AEB= ∠CEF$,$AE平分∠BAD$,求证:$∠B= ∠C$。
(1)若$∠EAD= 60^{\circ }$,求$∠DFE$的度数;
(2)若$∠AEB= ∠CEF$,$AE平分∠BAD$,求证:$∠B= ∠C$。

答案:
(1)
∵EF⊥AE,
∴∠AEF = 90°。
∵四边形AEFD的内角和是360°,∠D = 90°,∠EAD = 60°,
∴∠DFE = 360° - ∠D - ∠EAD - ∠AEF = 120°。
(2)
∵四边形AEFD的内角和是360°,∠AEF = 90°,∠D = 90°,
∴∠EAD + ∠DFE = 180°。
∵∠DFE + ∠CFE = 180°,
∴∠EAD = ∠CFE。
∵AE平分∠BAD,
∴∠BAE = ∠EAD。
∴∠BAE = ∠CFE。又
∵∠B + ∠BAE + ∠AEB = 180°,∠C + ∠CFE + ∠CEF = 180°,∠AEB = ∠CEF,
∴∠B = ∠C。
(1)
∵EF⊥AE,
∴∠AEF = 90°。
∵四边形AEFD的内角和是360°,∠D = 90°,∠EAD = 60°,
∴∠DFE = 360° - ∠D - ∠EAD - ∠AEF = 120°。
(2)
∵四边形AEFD的内角和是360°,∠AEF = 90°,∠D = 90°,
∴∠EAD + ∠DFE = 180°。
∵∠DFE + ∠CFE = 180°,
∴∠EAD = ∠CFE。
∵AE平分∠BAD,
∴∠BAE = ∠EAD。
∴∠BAE = ∠CFE。又
∵∠B + ∠BAE + ∠AEB = 180°,∠C + ∠CFE + ∠CEF = 180°,∠AEB = ∠CEF,
∴∠B = ∠C。
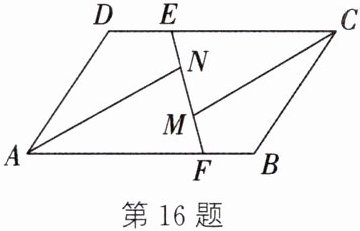
16. (8分)如图,在$□ ABCD的边AB$,$CD上截取AF$,$CE$,使得$AF= CE$,连结$EF$,$M$,$N是线段EF$上的两点,且$EM= FN$,连结$AN$,$CM$。
(1)求证:$\triangle AFN≌\triangle CEM$;
(2)若$∠CMF= 107^{\circ }$,$∠CEM= 72^{\circ }$,求$∠NAF$的度数。
(1)求证:$\triangle AFN≌\triangle CEM$;
(2)若$∠CMF= 107^{\circ }$,$∠CEM= 72^{\circ }$,求$∠NAF$的度数。

答案:
(1)
∵四边形ABCD是平行四边形,
∴CD//AB。
∴∠AFN = ∠CEM。在△AFN和△CEM中,
∵$\begin{cases}AF = CE\\\angle AFN = \angle CEM\\FN = EM\end{cases}$,
∴△AFN≌△CEM。
(2)由
(1),得△AFN≌△CEM,
∴∠NAF = ∠MCE。
∵∠CMF = ∠CEM + ∠MCE,∠CMF = 107°,∠CEM = 72°,
∴∠MCE = 35°。
∴∠NAF = 35°。
(1)
∵四边形ABCD是平行四边形,
∴CD//AB。
∴∠AFN = ∠CEM。在△AFN和△CEM中,
∵$\begin{cases}AF = CE\\\angle AFN = \angle CEM\\FN = EM\end{cases}$,
∴△AFN≌△CEM。
(2)由
(1),得△AFN≌△CEM,
∴∠NAF = ∠MCE。
∵∠CMF = ∠CEM + ∠MCE,∠CMF = 107°,∠CEM = 72°,
∴∠MCE = 35°。
∴∠NAF = 35°。
查看更多完整答案,请扫码查看


