《2025年暑期升级训练八年级数学浙教版浙江教育出版社》

1. 下列函数中,属于反比例函数的是 (A)
A.$ y = -\frac{2}{x} $
B.$ y = -\frac{x}{2} $
C.$ y = \frac{2}{x^{2}} $
D.$ y = \frac{2}{x + 2} $

答案： 解：反比例函数的一般形式为$y = \frac{k}{x}$（$k$为常数，$k≠0$，$x≠0$）。
- 选项A：$y = -\frac{2}{x}$，符合反比例函数的一般形式，其中$k = -2$。
- 选项B：$y = -\frac{x}{2}$是正比例函数。
- 选项C：$y = \frac{2}{x^2}$中$x$的次数是$2$，不是反比例函数。
- 选项D：$y = \frac{2}{x + 2}$不符合$y = \frac{k}{x}$的形式。
答案：A

2. (海南中考)若反比例函数 $ y = \frac{k}{x}(k \neq 0) $ 的图象经过点 $ (2, -3) $,则它的图象也一定经过的点的坐标是 (C)
A.$ (-2, -3) $
B.$ (-3, -2) $
C.$ (1, -6) $
D.$ (6, 1) $

答案： 解：因为反比例函数$y = \frac{k}{x}(k \neq 0)$的图象经过点$(2, -3)$，所以将$x = 2$，$y = -3$代入函数可得$-3=\frac{k}{2}$，解得$k = -6$，则反比例函数的解析式为$y = -\frac{6}{x}$。
分别将各选项代入解析式：
- 选项A：当$x=-2$时，$y=-\frac{6}{-2}=3\neq -3$，所以该点不在函数图象上。
- 选项B：当$x=-3$时，$y=-\frac{6}{-3}=2\neq -2$，所以该点不在函数图象上。
- 选项C：当$x=1$时，$y=-\frac{6}{1}=-6$，所以该点在函数图象上。
- 选项D：当$x=6$时，$y=-\frac{6}{6}=-1\neq 1$，所以该点不在函数图象上。
综上，答案选C。

3. (广安中考)若点 $ A(-3, y_{1}) $,$ B(-1, y_{2}) $,$ C(2, y_{3}) $ 都在反比例函数 $ y = \frac{k}{x}(k ＜ 0) $ 的图象上,则 $ y_{1} $,$ y_{2} $,$ y_{3} $ 的大小关系是 (A)
A.$ y_{3} ＜ y_{1} ＜ y_{2} $
B.$ y_{2} ＜ y_{1} ＜ y_{3} $
C.$ y_{1} ＜ y_{2} ＜ y_{3} $
D.$ y_{3} ＜ y_{2} ＜ y_{1} $

答案： A　解析:
∵ $ k ＜ 0 $，
∴ 反比例函数 $ y = \frac{k}{x} $ 的图象在二、四象限，且在每一象限内，y 随 x 的增大而增大。
∵ $ -3 ＜ 0 $，$ -1 ＜ 0 $，
∴ 点 $ A(-3, y_1) $，$ B(-1, y_2) $ 位于第二象限。
∴ $ y_1 ＞ 0 $，$ y_2 ＞ 0 $。
∵ $ -3 ＜ -1 ＜ 0 $，
∴ $ 0 ＜ y_1 ＜ y_2 $。
∵ $ 2 ＞ 0 $，
∴ 点 $ C(2, y_3) $ 位于第四象限。
∴ $ y_3 ＜ 0 $。
∴ $ y_3 ＜ y_1 ＜ y_2 $。
方法点金
利用反比例函数的性质比较函数值的大小
比较反比例函数的函数值的大小时，在同一分支上的点，可以通过比较其横坐标的大小来判断函数值的大小；不在同一分支上的点，根据与 x 轴的相对位置进行函数值大小的比较。另外，图象法和特殊值法也是解决此类问题的常见方法，图象法形象直观，特殊值法简单直接。

4. (张家界中考)在同一平面直角坐标系中,函数 $ y = kx + 1(k \neq 0) $ 和 $ y = \frac{k}{x}(k \neq 0) $ 的图象大致是 (D)

答案： 解：分两种情况讨论：
1. 当 $ k ＞ 0 $ 时：
一次函数 $ y = kx + 1 $ 的图象经过第一、二、三象限；
反比例函数 $ y = \frac{k}{x} $ 的图象经过第一、三象限。无符合选项。
2. 当 $ k ＜ 0 $ 时：
一次函数 $ y = kx + 1 $ 的图象经过第一、二、四象限；
反比例函数 $ y = \frac{k}{x} $ 的图象经过第二、四象限。符合选项 D。
答案：D

5. (荆州中考)如图所示为同一平面直角坐标系中的函数 $ y_{1} = 2x $ 和 $ y_{2} = \frac{2}{x} $ 的图象. 观察图象,可得不等式 $ 2x ＞ \frac{2}{x} $ 的解集为 (D)
A.$ -1 ＜ x ＜ 1 $
B.$ x ＜ -1 $ 或 $ x ＞ 1 $
C.$ x ＜ -1 $ 或 $ 0 ＜ x ＜ 1 $
D.$ -1 ＜ x ＜ 0 $ 或 $ x ＞ 1 $

答案： 解：联立方程$y_{1} = 2x$与$y_{2} = \frac{2}{x}$，得$2x=\frac{2}{x}$，
解得$x = 1$或$x=-1$。
观察函数图像：
当$-1 ＜ x ＜ 0$时，$y_{1}=2x$的图像在$y_{2}=\frac{2}{x}$的图像上方；
当$x ＞ 1$时，$y_{1}=2x$的图像在$y_{2}=\frac{2}{x}$的图像上方。
所以不等式$2x＞\frac{2}{x}$的解集为$-1 ＜ x ＜ 0$或$x ＞ 1$。
答案：D

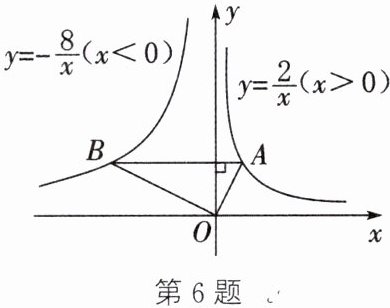
6. (郴州中考)如图,在函数 $ y = \frac{2}{x}(x ＞ 0) $ 的图象上任取一点 $ A $,过点 $ A $ 作 $ y $ 轴的垂线,交函数 $ y = -\frac{8}{x}(x ＜ 0) $ 的图象于点 $ B $,连结 $ OA $,$ OB $,则 $ \triangle AOB $ 的面积是 ( )

A.3
B.5
C.6
D.10

答案：
B解析:如图,记AB交y轴于点C。
∵点A在函数 $ y = \frac{2}{x}(x ＞ 0) $ 的图象上，
∴ $ S_{\triangle AOC} = \frac{1}{2} × 2 = 1 $。又
∵ 点B在函数 $ y = -\frac{8}{x}(x ＜ 0) $ 的图象上，
∴ $ S_{\triangle BOC} = \frac{1}{2} × 8 = 4 $。
∴ $ S_{\triangle AOB} = S_{\triangle AOC} + S_{\triangle BOC} = 1 + 4 = 5 $。
　　　　　
方法点金
巧用反比例函数的比例系数“K”的几何意义解题反比例函数的比例系数“k”具有一定的几何意义，过反比例函数 $ y = \frac{k}{x}(k \neq 0) $ 的图象上任意一点向两坐标轴作垂线段，则垂线段与两坐标轴所围成的矩形的面积等于 $ |k| $。在反比例函数的图象中，涉及三角形或矩形的面积时，常用比例系数“k”的几何意义求解。

7. 新趋势 与物理融合 (丽水中考)已知电灯两端的电压 $ U $ 为 $ 220V $,通过灯泡的电流 $ I $ 的最大限度不得超过 $ 0.11A $. 设选用灯泡的电阻为 $ R $,下列说法中,正确的是 (A)
A.$ R \geq 2000\Omega $
B.$ R \leq 2000\Omega $
C.$ R \geq 24.2\Omega $
D.$ R \leq 24.2\Omega $

答案： 解：根据欧姆定律 $ I = \frac{U}{R} $，可得 $ R = \frac{U}{I} $。
已知 $ U = 220V $，$ I \leq 0.11A $，则 $ R = \frac{220}{I} $。
当 $ I $ 最大为 $ 0.11A $ 时，$ R $ 最小，$ R_{\text{min}} = \frac{220}{0.11} = 2000\Omega $。
因为电流 $ I $ 不得超过 $ 0.11A $，所以电阻 $ R $ 不得小于 $ 2000\Omega $，即 $ R \geq 2000\Omega $。
答案：A

8. 某校对教室采用药熏消毒,已知药物燃烧时,室内空气中每立方米的含药量 $ y $(毫克)与燃烧时长 $ x $(分钟)成正比例,药物燃烧完后,$ y $ 与 $ x $ 成反比例(如图). 现测得药物 8 分钟燃烧完,此时室内空气中每立方米的含药量为 6 毫克. 研究表明,当空气中每立方米的含药量不低于 3 毫克时,药熏消毒才有效. 此次消毒的有效时长为 (B)
A.10 分钟
B.12 分钟
C.14 分钟
D.16 分钟

答案： B解析:易得题中的正比例函数与反比例函数的表达式分别为 $ y = \frac{3}{4}x(0 \leq x \leq 8) $ 和 $ y = \frac{48}{x}(x ＞ 8) $。把 $ y = 3 $ 代入 $ y = \frac{3}{4}x $，得 $ x = 4 $；把 $ y = 3 $ 代入 $ y = \frac{48}{x} $，得 $ x = 16 $。
∵ $ 16 - 4 = 12 $（分钟），
∴ 此次消毒的有效时长为12分钟。
易错提示
忽略自变量取值范围的“分界点”
一次函数与反比例函数的综合实际应用题，一般包含着两个时段的函数关系，因此在求两个函数表达式时要特别注意图象中的折点（即公共点），它既可以用来确定一次函数和反比例函数的表达式，又是自变量的取值范围的分界点。例如本题中的折点 $ (8, 6) $，由此我们可以确定正比例函数和反比例函数的表达式及函数中的自变量 x 的取值范围。

9. (福建中考)已知反比例函数 $ y = \frac{k}{x} $ 的图象分别位于二、四象限,则实数 $ k $ 的值可以是-3(写出一个即可).

答案： 解：因为反比例函数$y = \frac{k}{x}$的图象分别位于二、四象限，所以$k ＜ 0$，则实数$k$的值可以是$-3$。
$-3$