第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 用两块相同的三角板拼出形状不同的平行四边形能拼(
A.3个
B.3个或4个
C.4个
D.2个或3个
A
)A.3个
B.3个或4个
C.4个
D.2个或3个
答案:
A
2. 如图,点A,B,C,D,E,F在同一平面内,连接AB,BC,CD,DE,EF,FA,若$∠BCD= 110^{\circ }$,则$∠A+∠B+∠D+∠E+∠F$等于(
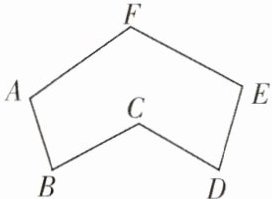
A.$470^{\circ }$
B.$450^{\circ }$
C.$430^{\circ }$
D.$410^{\circ }$
A
)
A.$470^{\circ }$
B.$450^{\circ }$
C.$430^{\circ }$
D.$410^{\circ }$
答案:
A
3. 如图,点E为$□ ABCD$内一点,连接EA,EB,EC,ED,AC,已知$\triangle BCE$的面积为2,$\triangle CED$的面积为10,则阴影部分$\triangle ACE$的面积为(
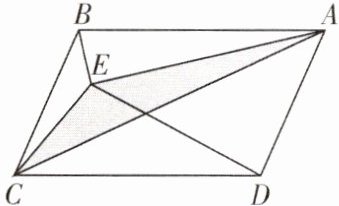
A.6
B.8
C.10
D.12
B
)
A.6
B.8
C.10
D.12
答案:
B
4. 一个多边形截去一个角后,形成另一个多边形的内角和为$720^{\circ }$,那么原多边形的边数为(
A.5
B.5或6
C.6或7
D.5或6或7
D
)A.5
B.5或6
C.6或7
D.5或6或7
答案:
D
5. 下列说法不正确的是(
A.五边形的外角和为$360^{\circ }$
B.三角形的外角大于任何一个与它不相邻的内角
C.两条直线被第三条直线所截,同旁内角互补
D.三角形的三条高至少有一条在三角形内
C
)A.五边形的外角和为$360^{\circ }$
B.三角形的外角大于任何一个与它不相邻的内角
C.两条直线被第三条直线所截,同旁内角互补
D.三角形的三条高至少有一条在三角形内
答案:
C
6. 如图,在五边形ABCDE中,$∠A= ∠B= ∠C= ∠D= 120^{\circ }$,且$AB= 2$,$BC= 4$,$CD= 3$,下列结论:①$AB// DE$;②$AE= DE$;③五边形ABCDE的面积为$17\sqrt {3}$.其中正确的是(

A.①②
B.①③
C.②③
D.①②③
B
)
A.①②
B.①③
C.②③
D.①②③
答案:
B
7. 如图,在平行四边形ABCD中,以BC和AD为斜边分别向内作等腰直角$\triangle BCE和等腰直角\triangle ADG$,延长BE和DG分别交AG和CE于H,F两点,直线FH分别交AD和BC于I,J两点.若四边形EFGH是正方形,$IJ= 6\sqrt {2}$,则平行四边形ABCD的面积是(

A.24
B.36
C.48
D.72
D
)
A.24
B.36
C.48
D.72
答案:
D
8. 延时课上,王林用四根长度都为4cm的木条制作了如图1所示的正方形,而后将正方形的BC边固定,平推成如图2的图形,并测得$∠B= 60^{\circ }$,则在此变化过程中,下列结论错误的是(

A.AB长度不变,为4cm
B.AC长度变小,减少$4(\sqrt {2}-1)cm$
C.BD长度变大,增加$4(\sqrt {3}-\sqrt {2})cm$
D.四边形面积减少$8(\sqrt {3}-1)cm^{2}$
D
)
A.AB长度不变,为4cm
B.AC长度变小,减少$4(\sqrt {2}-1)cm$
C.BD长度变大,增加$4(\sqrt {3}-\sqrt {2})cm$
D.四边形面积减少$8(\sqrt {3}-1)cm^{2}$
答案:
D
查看更多完整答案,请扫码查看


